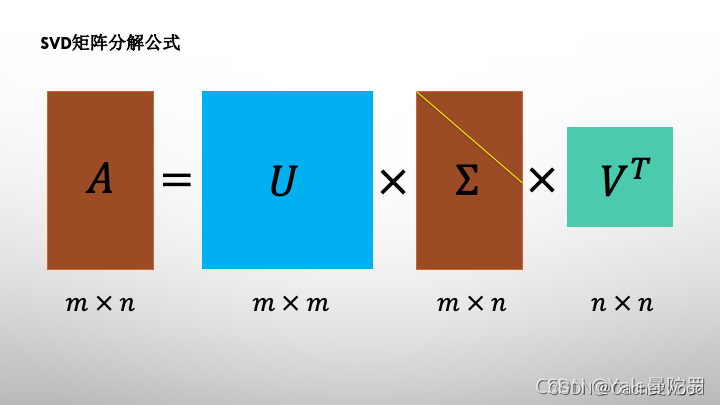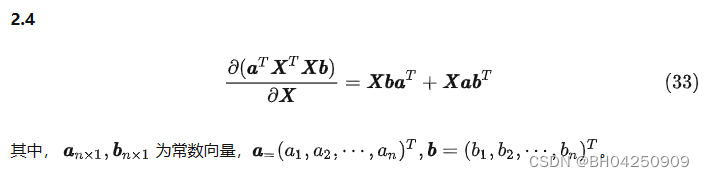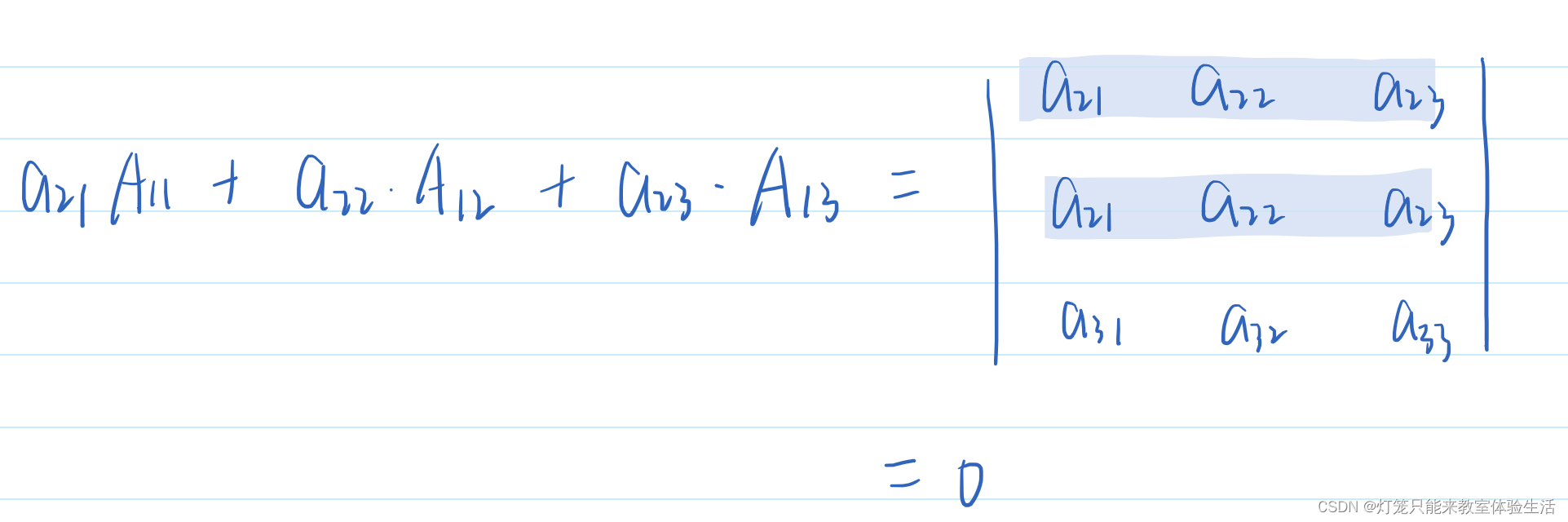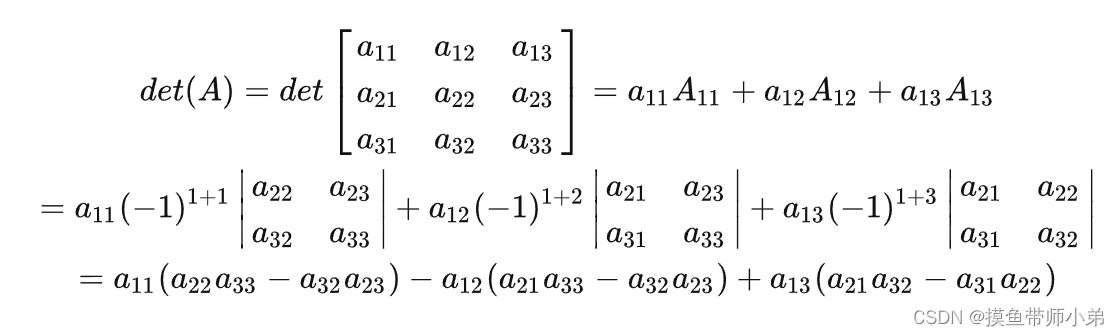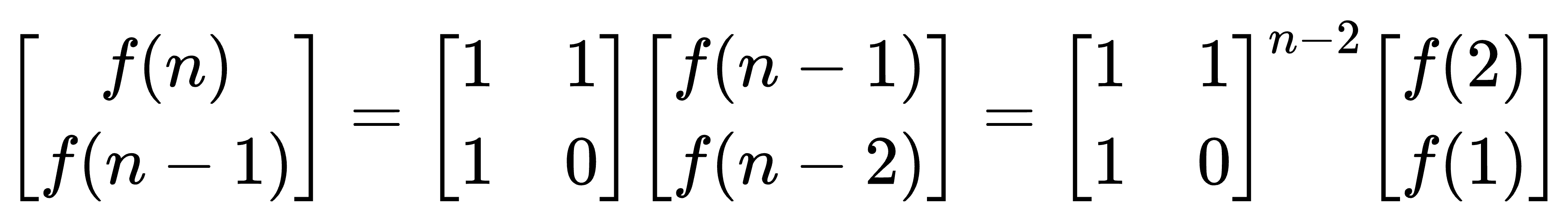物联网
python快速入门
经验
硬件工程
rabbitmq
javaweb
尚品汇
开发板
虚拟设备
#产品思维
漏洞
decodeByteArray
球形消息传递
ras
cdh
相机参数
手机浏览器
普林斯顿大学
应力强度因子
QA
线性代数
2024/4/11 13:42:57推荐系统——排序算法综述
常见排序算法有:
目录
一、传统算法
二、特征工程深度模型
三、多目标学习模型
四、Pointwise、Pairwise、ListWise 排序架构: 一、传统算法
1、LR
2、GBDT、XGBoost、LightGBM
具体原理见:传统机器学习算法_码一…
数值分析(12):Rung-Kutta法及单步法的收敛性和稳定性分析
Rung-Kutta法及单步法的收敛性和稳定性分析1. 引言2. Runge-Kutta法2.1 一阶RK方法2.2 二阶RK方法2.3 三阶RK方法2.4 四阶RK方法3. 单步法收敛性和稳定性3.1 收敛性3.2 相容性3.3 稳定性1. 引言
在《数值分析(11):常微分方程的数值解法之Euler法》中已经介绍了常微…
【回归分析】01. 随机向量(1)
文章目录【回归分析】1. 随机向量(1)2.1 均值向量与协方差阵2.2 随机向量的二次型2.3 正态随机向量【回归分析】1. 随机向量(1)
2.1 均值向量与协方差阵
当用矩阵形式来表示一个线性模型时,观测向量和误差向量都是随机向量。 均值向量:设 X(X1,X2,⋯,X…
拉格朗日差值法python实现
Lagrange插值法:Lagrange插值法:Lagrange插值法:给定一组点(x1,y1),(x2,y2)...(xn,yn)给定一组点 (x_{1},y_{1}),(x_{2},y_{2})...(x_{n},y_{n})给定一组点(x1,y1),(x2,y2)...(xn,yn)n次拉格朗日插值基函数Pi(x)∏j1,j≠inx−xjx…
多项式插值算法 python实现
算法思想:用多项式逼近原函数
import numpy as np
from numpy import *
import numpy.linalg as lg #numpy的线性代数函数库 linalg
import math
x[]
y[]
N10
pimath.pi
#形成十个(x,y)点
for i in range(N):x.append(round((-1(2/N)*(N-i)),3))
de…
lagrange插值法、多项式插值法习题---python实践
1.等分点、lagrange插值法 lagrange算法实现参考我的 拉格朗日差值法python实现 文章 b站视频教程:https://www.bilibili.com/video/BV14Z4y1z78B?share_sourcecopy_web
import numpy
import matplotlib
import math
from matplotlib import pyplot
import time
N…
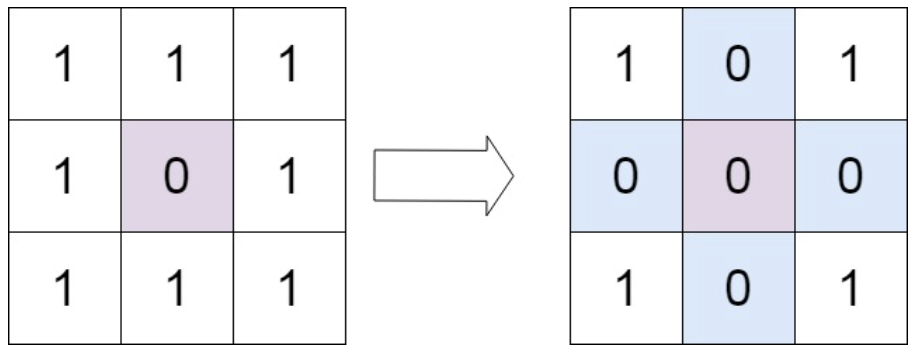
【2373. 矩阵中的局部最大值】
来源:力扣(LeetCode)
描述:
给你一个大小为 n x n 的整数矩阵 grid 。
生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足:
maxLocal[i][j] 等于 grid 中以 i 1 行和 j 1 列为中心的 3 …
线性代数学习笔记(十六)——初等变换(二)
本篇笔记首先介绍了初等方阵的定义、初等变换和初等方阵的关系、初等方阵求行列式、初等方阵求逆矩阵以及初等方阵求转置;然后介绍了初等方阵的用处,以及任意矩阵、初等矩阵和标准形之间的关系;最后介绍了矩阵可逆的两个充分必要条件…
线性代数学习笔记(二十八)——齐次方程组的解
本篇笔记通过回顾线性方程组解的判定,引出并讨论了齐次线性方程组解的情况;然后通过上一章节的定理总结出几个推论并做了一定的讨论;最后通过求齐次线性方程组的例子来判断向量组的相关性,同时求解一组相关系数。
1 回顾
前面讨…
线性代数Python计算:向量的模及向量间的夹角
numpy的dot函数计算两个向量α\boldsymbol{\alpha}α和β\boldsymbol{\beta}β的内积: dot(a,b)\text{dot(a,b)}dot(a,b) 两个参数a和b表示参与计算的两个表示为数组的向量α\boldsymbol{\alpha}α和β\boldsymbol{\beta}β,函数返回值α∘β\boldsymbol…
线性代数Python计算:二次型的标准形计算
为寻求正交变换yPTx\boldsymbol{y}\boldsymbol{P}^\text{T}\boldsymbol{x}yPTx,使得二次型fxTAxf\boldsymbol{x}^\text{T}\boldsymbol{Ax}fxTAx的标准形为fyTΛyf\boldsymbol{y}^\text{T}\boldsymbol{\Lambda y}fyTΛy,其中Λ\boldsymbol{\Lambda}Λ为一…
LA@相似对角化判定定理和计算方法
文章目录 方阵相似对角化引言相似对角化变换矩阵的性质构造对角化变换矩阵 方阵可对角化判定定理🎈推论:无重根特征值的方阵可以对角化含重根特征值的方阵的对角化判定定理总结👺 综合:对角化步骤归纳例特征值计算构造相似变换阵下结论 方阵相似对角化
…
NOI2021信息竞赛学习笔记
一.图论
1.仙人掌问题(圆方树)
2.矩阵树定理
3.网络流
4.基环树 二、数据结构
1.线段树
2.左偏树
3.树链剖分
4.主席树
5.树套树
6.长链剖分
7.LCT 三、数学
1.欧拉函数|(扩展)欧拉定理|欧拉反演
2.线性筛
3.莫比乌…
[工程数学]1_特征值与特征向量
首先向b站up,DR_CAN致敬。
视频二刷了,为了收获,理解更多,用极慢的方式,把笔记抄了下来,整理一遍,为了好翻阅。后续会转成pdf格式,放微信公众号后台获取。
[现代控制理论]2_state-…
线性回归解析解推导以及实现
公式1: w1∗∑iyi(xi−1n∑ixi)∑ixi2−1n(∑ixi)2w_1^*\frac{\sum_i y_i(x_i-\frac{1}{n}\sum_i x_i)}{\sum_i x_i^2-\frac{1}{n}(\sum_ix_i)^2} w1∗∑ixi2−n1(∑ixi)2∑iyi(xi−n1∑ixi) 推导上式,给定以下条件࿱…
[解题报告]【第33题】给定一个 n X n 的矩阵,求它的转置矩阵
全文目录🎁主要知识点矩阵的转置📓课后习题867. 转置矩阵📑写在最后今天是c语言基础打卡的第33天,主要内容是矩阵的操作,还牵扯了亿点点二级指针的相关知识点,希望大家能够理解呢。
相关链接: 【第33题】给…
[解题报告]【第34题】给定一个 n X n 的矩阵 和 R,求旋转 90R 度以后的矩阵
全文目录🎁主要知识点矩阵的旋转📓课后习题48. 旋转图像📑写在最后今天是c语言基础打卡的第34天,主要内容是矩阵的操作,希望大家能够理解呢,我就给大家记一下重点,给点课后题提示0.0。
相关链接࿱…
[解题报告]《算法零基础100讲》(第1讲) 幂和对数
☘前言☘
今天是算法零基础打卡的第1天,大家先熟悉一下感觉,课后题我给大家亿点点参考。上链接: 《算法零基础100讲》(第1讲) 幂和对数 🧑🏻作者简介:一个从工业设计改行学嵌入式的年轻人 ✨联系方式&…
【解题报告】《LeetCode零基础指南》(第八讲) 二维数组
☘前言☘
今天是九日集训第七天,我会记录一下学习内容和题解,争当课代表0.0. 链接:《LeetCode零基础指南》(第八讲) 二维数组 🧑🏻作者简介:一个从工业设计改行学嵌入式的年轻人 ✨联系方式:22…
第6关:复数及math库的应用
from math import exp,sqrt,radians,sin,cos,pi
x53j
yexp(sqrt(pi/4))
#exp(e的x次方)
#sqrt(根号x)
#pi(π)
aradians(56)
#radians(将角度转换为弧度)
pabs(xy)
z2*sin(a)/(xcos(p))
#sin&cos(三角函数)
print("…
GPS从入门到放弃(二十五)、卡尔曼滤波
一、概述
单点定位的结果因为是单独一个点一个点进行的,所以连续起来看数据可能出现上串下跳的情况,事实上并不符合实际情况。为了解决这个问题,考虑到物体运动的连续性和运动变化的缓慢性,可以通过滤波器来平滑位置轨迹。 滤波器…
MATLAB 和 Python 建模和仿真
特点
首先介绍了建模及其对当前科学和工程实践的重要性介绍了每个编程环境和用于表示变量和计算数学方程和函数的语法
内容
计算模型介绍 计算科学重要性建模如何促进科学和工程的进步建模过程 编程环境介绍 MATLAB编程环境Python 环境 确定性线性模型 模型选择数学表示线性…
CF618G Combining Slimes 题解
CF618G Combining SlimesCF618G Combining Slimes 首先考虑根据期望的线性性质对于每一个数分开来计算贡献,之后再求出每一个数出现的概率即可。 也不是很清楚这个东西是不是线性性质。 但是说实话就是对于所有数一起考虑是不能入手的。 之后我们发现事实上任意的数…
[NOI2013] 矩阵游戏 题解
[NOI2013] 矩阵游戏[NOI2013] 矩阵游戏 各位我是弱智石锤了。 题目可能不是很难但是有点细节要注意。
首先考虑行和列我们分别来看:
对于列的情况我们只需要前一项即可递推。对于行的情况我们只需要上一项也可递推。
那么本质上题目就提示我们可以只保留一项进行…
python 矩阵乘法
一 np.dot()
同线性代数中矩阵乘法的定义。np.dot(A, B)表示:
对二维矩阵,计算真正意义上的矩阵乘积。对于一维矩阵,计算两者的内积。
import numpy as np# 2-D array: 2 x 3
two_dim_matrix_one np.array([[1, 2, 3], [4, 5, 6]])
# 2-D…
常用导航坐标系 及 转换关系 (理论+程序)
一、坐标系定义与符号约定 在捷联惯导中,涉及到多种坐标系,其中 惯性坐标系、地心地固坐标系、导航坐标系 的示意图如下:下面给出常用的坐标系的定义: 1)惯性坐标系(i 系): 以地球质…
非线性最小二乘法之Gauss Newton、L-M、Dog-Leg9
最优化理论非线性最小二乘
最优化理论非线性最小二乘_努力努力努力-CSDN博客 最快下降法
理解: a*b |a|*|b|*cos() 最小二乘问题
通常的最小二乘问题都可以表示为: GaussNewton close all;
clc;a1;b2;c1; %待求解的系数x(0:0.01:1);
w…
线性最小二乘和非线性最小二乘
本文基于下面的博客,结合自己第一次看的时候的一些问题,重新梳理总结一下 https://blog.csdn.net/wsj998689aa/article/details/41558945 先理解这个博客的内容
最小二乘通俗解释_AplusX-CSDN博客_最小二乘法 一:什么是最小二乘 注意&#x…
参考系列2:优化库——ceres(一)快速概览
目录
1 📖 ceres快速概览
1.1 🔖问题建模和求解
1.1.1 问题建模 1.1.2 问题求解
1.2 :🔖ceres使用流程
1.3 🔖 求导方法:构建代价函数(STEP2)
1.3.1 解析求导(自定义求导&…
算法性能分析(5):递归算法的时间与空间复杂度分析
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列࿱…
机器视觉(六)——像素坐标系、图像坐标系、相机坐标系以及世界坐标系
机器视觉(六)——像素坐标系、图像坐标系、相机坐标系以及世界坐标系 目录1. 像素坐标系2. 图像坐标系3.相机坐标系4.世界坐标系1. 像素坐标系
如下图所示:像素坐标系u-v的原点为O0, 横坐标u和纵坐标v分别是图像所在的行和列&…
GPS从入门到放弃(一)、GPS 定位原理
GPS,全称 Global Positioning System,已经广泛应用于我们的日常生活中了,现在的智能手机 里都会自带GPS定位功能。这是一个美国的全球定位系统,虽然我们现在也有北斗了,但毕竟GPS搞的早,所以先从它开始研究…
ublox f9p,Realsense D435i相关资料
一、Realsense D435i使用笔记
1、Realsense D435i使用笔记
2、Inter Realsense D435i标定详细步骤_高喜天天的博客-CSDN博客
3、Realsense D435i深度测距和普通摄像头单目测距的区别(附带可用实测代码) 4、Realsense D435i学习资料汇总
5、从零开始使用Realsense D435i运行…
GPS从入门到放弃(二十二)、站点位移
站点位移(Site Displacements)是固定在地球上的站点因为地球潮汐等因素影响跟随地球表面一起运动而造成的站点在地固坐标系(可参考坐标系一文)中的位移。 虽然我们一般把地球看着一个固体,但它却不是一个刚体ÿ…
矩阵在3d世界的重要作用
opengl学习链接 😕/learnopengl-cn.github.io/01%20Getting%20started/07%20Transformations/
旋转
上面几个的变换内容相对容易理解,在2D或3D空间中也容易表示出来,但旋转(Rotation)稍复杂些。如果你想知道旋转矩阵是如何构造出来的&#…
技术短视频账号矩阵seo系统--源头开发---saas工具
专注短视频账号矩阵系统源头开发---saas营销化工具,目前我们作为一家纯技术开发团队目前已经专注打磨开发这套系统企业版/线下版两个版本的saas营销拓客工具已经3年了,本套系统逻辑主要是从ai智能批量剪辑、账号矩阵全托管发布、私信触单收录、文案ai智能…
GAMS建模技术案例01 求解简单的线性规划模型
目录
1.问题描述
2 GAMS代码要点
2.1 代码编写要点
2.2 案例源码
2.3 计算结果及报告解 1.问题描述
首先给出一个基本线性规划问题的计算案例 subject to: 2 GAMS代码要点
2.1 代码编写要点
使用 * 表示注释文本定义变量 Positive Variable 表示定义非负变量Negative V…
【考研数学】数学“背诵手册”(二)| 线代及概率论部分
文章目录 引言二、线代施密特正交化分块矩阵转置、逆、伴随之间的运算关于秩定义性质 三、概统常见分布的期望及方差 引言
这数一全部内容太多了,放在一篇文章里的话,要编辑就很困难,就把线代和概率放在这篇文章里吧。 二、线代
施密特正交…
大数据HCIE成神之路之数学(2)——线性代数
线性代数 1.1 线性代数内容介绍1.1.1 线性代数介绍1.1.2 代码实现介绍 1.2 线性代数实现1.2.1 reshape运算1.2.2 转置实现1.2.3 矩阵乘法实现1.2.4 矩阵对应运算1.2.5 逆矩阵实现1.2.6 特征值与特征向量1.2.7 求行列式1.2.8 奇异值分解实现1.2.9 线性方程组求解 1.1 线性代数内…
线性代数-Python-01:向量的基本运算 - 手写Vector及numpy的基本用法
文章目录 一、代码仓库二、向量的基本运算2.1 加法2.2 数量乘法2.3 向量运算的基本性质2.4 零向量2.5 向量的长度2.6 单位向量2.7 点乘/内积:两个向量的乘法 --答案是一个标量 三、手写Vector代码3.1 在控制台测试__repr__和__str__方法3.2 创建实例测试代码3.3 完整…
用excel计算矩阵的乘积
例如,我们要计算两个矩阵的乘积,
第一个矩阵是2*2的:
1234
第2个矩阵是2*3的:
5697810 在excel中鼠标点到其它空白的地方,用来存放矩阵相乘的结果: 选择插入-》函数: 选中MMULT,…
矩阵理论--矩阵分解
矩阵理论–矩阵分解
矩阵的三角分解、谱分解、最大秩分解、奇异值分解的操作步骤,以及相关说明。
1、QR分解
(1)非奇异方阵
方阵(非奇异):将方阵分解成酉矩阵左乘正线上三角,或者酉矩阵右乘…
线性代数-Python-02:矩阵的基本运算 - 手写Matrix及numpy中的用法
文章目录 一、代码仓库二、矩阵的基本运算2.1 矩阵的加法2.2 矩阵的数量乘法2.3 矩阵和向量的乘法2.4 矩阵和矩阵的乘法2.5 矩阵的转置 三、手写Matrix代码Matrix.pymain_matrix.pymain_numpy_matrix.py 一、代码仓库 https://github.com/Chufeng-Jiang/Python-Linear-Algebra-…
06 - 逆矩阵、列空间与零空间
06 - 逆矩阵、列空间与零空间
回到目录 尽管我们从几何的角度理解线性代数,但是线性代数的起源并不是这样,而是起源于解方程组。这也是它当今最有用的用途之一。 比如下面这个方程组它只具有常系数,并且只进行加法,没有x^2或者s…
线性代数矩阵转置乘法_单位矩阵转置属性| 使用Python的线性代数
线性代数矩阵转置乘法Prerequisites: 先决条件: Defining a matrix 定义矩阵 Identity matrix 身份矩阵 Transpose matrix 转置矩阵 In linear algebra, the identity matrix, of size n is the n n square matrix with ones on the main diagonal and zeros else…
基于LDA的隐式标签协同过滤推荐算法_文勇军
, 王全民等人[14]提出了一种交替奇异值分解算法 (ASVD),即结合协同过滤和隐语义分析的混合推荐 算法。唐泽坤等人[15]融合聚类算法和协同过滤推荐 算法,取得了一定效果。高娜等人[16⁃19]将标签因子 和协同过滤推荐算法结合研究缓解了数据稀疏问题,但这…
【PTA题目】7-1 求矩阵各行元素之和 (15 分)
本题要求编写程序,求一个给定的mn矩阵各行元素之和。
输入格式:
输入第一行给出两个正整数m和n(1≤m,n≤6)。随后m行,每行给出n个整数,其间
以空格分隔。
输出格式:
每行输出对应矩阵行元素…
船舶运动野本模型求解
(1)
r为艏摇角速度
拉普拉斯变换,得 r0为初值
设舵角输入量为零时刻的阶跃输入,幅值为n,拉式变换为 代入上式,得 拉普拉斯反变换得 python直接求解式(1)
import math
import numpy as np
from scipy.in…
05:计算鞍点http://www.noi.openjudge.cn/
05:计算鞍点
查看提交统计提问
总时间限制:
1000ms 内存限制:
65536kB
描述
给定一个5*5的矩阵,每行只有一个最大值,每列只有一个最小值,寻找这个矩阵的鞍点。 鞍点指的是矩阵中的一个元素,它是所在行的最大值,…
09:矩阵乘法http://www.noi.openjudge.cn/
09:矩阵乘法
查看提交统计提问
总时间限制:
1000ms 内存限制:
65536kB
描述
计算两个矩阵的乘法。n*m阶的矩阵A乘以m*k阶的矩阵B得到的矩阵C 是n*k阶的,且C[i][j] A[i][0]*B[0][j] A[i][1]*B[1][j] …… A[i][m-1]*B[m-1][j](C[i][j]表示C矩阵中第i行第j列…
行满秩矩阵为何变成增广矩阵还为满秩
标题一:从性质上看
由于mn 的矩阵的秩r<min{m,n}. 所以既然是行满秩,那么 rm, 且m<n. 它的增广阵就是m(n1), 增广的秩< min{m,n1}, 由上面的m<n, 得到m<n1, 所以增广阵的秩最大为m。 又 增广的秩一定 大于等于 系数阵的秩r,因…
796. 子矩阵的和(左上角前缀和)
题目:
796. 子矩阵的和 - AcWing题库 思路:
1.暴力搜索(搜索时间复杂度为O(n2),很多时候会超时)
2. 前缀和(左上角前缀和):本题特殊在不是直接求前n个数的和,而是求…
线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录
1,矩阵定义
2,矩阵的运算
3,方阵的行列式和伴随矩阵
4,矩阵的逆
5,克莱默法则
6,矩阵分块 1,矩阵定义
矩阵与行列式的区别:
(1)形式上行列式…
方阵的特征值、特征向量以及特征多项式和特征方程
方阵的特征值、特征向量以及特征多项式和特征方程
一、 特征值和特征向量
定义:设 A \bf A A是 n n n阶矩阵,如果数 λ \lambda λ和 n n n维非零列向量 x \bf x x使得关系式 A x λ x (1a) {\bf{Ax }}\lambda {\bf{x}} \tag{1a} Axλx(1a) 成立&…
线性代数 为什么齐次线性方程有非零解的充要条件是系数行列式不等于零?
因为齐次线性方程一定存在零解(齐次线性方程组为AX0,其中A为矩阵),而系数行列式不等于零那么线性方程必然只有1个解组(0),所以对于齐次方程来说有非0解则系数行列式一定要等于零。
求解步骤
1、对系数矩阵…
【LeetCode】旋转图像(原地算法,找规律)
旋转图像(找规律) 题目链接:https://leetcode-cn.com/problems/rotate-image/ 题目大意:将矩阵顺时针旋转90度,要求原地旋转,空间复杂度O(1) 先水平对折翻转,然后主对角线翻转 func rotate(matrix [][]int) {n:len(ma…
机器学习中的数学知识1——导数、向量、偏导与梯度
数学是机器学习的基础,各种算法需要大量使用微积分,线性代数,概率论,最优化方法等数学知识,特别是最优化理论,可以说机器学习中的大多数算法研究到最后都是一个数学优化问题。接下来将一一介绍机器学习中的…
CF1182E Product Oriented Recurrence 题解
CF1182E Product Oriented RecurrenceCF1182E Product Oriented Recurrence 看到这个 nnn 很大就会直接考虑矩阵乘法。
我们直接把指数拿下来即可,分成两部分进行计算。
对于 ccc 的部分有这样的矩阵: [c1c2c32n−62][0010010100011000011000011]\left…
从浅到深研究矩阵的特征值、特征向量
本篇特征值、特征向量笔记来源于MIT线性代数课程。 矩阵特征值与特征向量 ✨引言✨什么是特征向量呢?✨表示✨从特例看特征值与特征向量✨如何求解方程▶️ 思路:✨对称矩阵例子:✨对比观察两个矩阵及它们的特征值及特征向量:✨旋…
第六章,线性变换,1-线性变换、表示矩阵、线性算子
第六章,线性变换,1-线性变换、表示矩阵、线性算子 线性变换表示矩阵 线性算子 R 2 R^2 R2中特殊的线性变换旋转变换算子反射变换算子投影变换算子伸压变换算子剪切变换算子 玩转线性代数(32)线性变换的相关概念的笔记,相关证明以及例子见原文…
CF917C Pollywog 题解
CF917C PollywogCF917C Pollywog 发现 xxx 是比较小的我们考虑直接状压。
之后发现 nnn 是比较大的考虑使用矩阵加速进行运算。
矩阵加速其实不一定只能使用加减,使用 min,max\min, \maxmin,max 也是可以的,具体来说需要满足一些性质。
我们不妨设…
线性代数Python计算:线性变换的值域与核
设数域PPP上的向量空间PnP^nPn的线性变换TTT,在某个基下其变换矩阵A(α1,α2,⋯,αn)\boldsymbol{A}(\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_n)A(α1,α2,⋯,αn)。TTT的值域T(Pn)T(P^n)T(Pn)为α1,α2,⋯,α1\boldsymbol{…
线性代数的学习和整理15:线性代数的快速方法
1 数学/线性代数里,其实很多东西的求得都有多种解决办法 很多概念,界定狠清晰,但是不好求
多种方法,拓宽思维 方法1:按定义直接去求解
方法2:按 2 比如求逆矩阵
概念方法,线性变化
增广矩阵…
求与矩阵相似的三角矩阵
要求一个矩阵与给定矩阵相似,可以通过将该矩阵对角化的方法来实现。对角化的过程可以分解为两个步骤:首先找到该矩阵的特征值和特征向量,然后将特征向量按列组成的矩阵和一个对角矩阵相乘,得到相似的对角矩阵。
如果要求与矩阵 A…
线性代数 - 几何原理
目录 序言向量的定义线性组合、张成空间与向量基线性变换和矩阵线性复合变换与矩阵乘法三维空间的线性变换行列式矩阵的秩和逆矩阵维度变换点乘叉乘基变换特征值和特征向量抽象向量空间 序言 欢迎阅读这篇关于线性代数的文章。在这里,我们将从一个全新的角度去探索线…
Eigen中几种表示三维位姿的方式以及相互转换
本文属于转发,感谢:Eigen中几种表示三维位姿的方式以及相互转换_鸿哲闲居的博客-CSDN博客_isometry3d 目录
一、位姿的表示方式
1. 普通4*4矩阵 Eigen::Matrix
2. 等距映射:Eigen::Isometry3d
二、旋转的表示方式与相互转换
1. 四元数的…
特殊的矩阵与特殊的矩阵关系———实对称、正定、对角、零矩阵
一、特殊的矩阵 1、实对称矩阵 定义:都是实数,且 性质: (1)可以用特征值来求A的大小 (2)可以得到A的秩 (3)必定可以相似对角化 运用: 与实对称矩阵A合同的矩…
线性代数-Python-03:矩阵的变换 - 手写Matrix Transformation及numpy中的用法
文章目录 一、代码仓库二、旋转矩阵的推导及图形学中的矩阵变换2.1 让横坐标扩大a倍,纵坐标扩大b倍2.2 关于x轴翻转2.3 关于y轴翻转2.4 关于原点翻转(x轴,y轴均翻转)2.5 沿x方向错切2.6 沿y方向错切2.7 旋转2.8 单位矩阵2.9 矩阵的…
程序员的自我修养之数学基础02:向量(向量的运算、模、夹角、距离和Python实现)
1. 什么是向量?
数学概念嘛,在不同的应用场景下意义是不大一样的,比如说对于机械或者物理的同学,向量是有长度有方向的一个指向空间的带箭头的线段,而对于从事计算机工作的我们来说,向量的定义可以是非常简…
MarkdownPad2, CSDN及有道云笔记对数学公式的支持
MarkdownPad2, CSDN及有道云笔记对数学公式的支持
MarkdownPad2的安装
下载并安装MrakdownPad2软件,下载地址安装awesomium_v1.6.6_sdk_win, 下载地址安装支持公式编辑的插件,注意,在MarkdownPad2的 Tools > Options > Ad…
线性代数(五) | 矩阵对角化 特征值 特征向量
文章目录 1 矩阵的特征值和特征向量究竟是什么?2 求特征值和特征向量3 特征值和特征向量的应用4 矩阵的对角化 1 矩阵的特征值和特征向量究竟是什么?
矩阵实际上是一种变换,是一种旋转伸缩变换(方阵) 不是方阵的话还有可能是一种…
不动点定理的及其有趣应用
最近读高观点下的数学这本书,对书中介绍的布劳威尔不动点定理的有趣性质印象很深,原因是这个定理的某些性质能够解释我们生活中的一些常见现象,这里结合一个例题,聊以记录。
从一个数学题讲起:
f(x)是定义在[0,1]上的…
奇异值分解SVD的定义,求法,推导和几何意义以及它和各位伪逆矩阵的关系
定义
奇异值分解就是把一个矩阵分解成正交矩阵乘以对角矩阵乘以正交矩阵的形式,即 即 A U Σ V T AU\Sigma V^T AUΣVT
求法 A A T U Σ V T V Σ U T U Σ 2 U T AA^TU\Sigma V^TV\Sigma U^TU\Sigma^2U^T AATUΣVTVΣUTUΣ2UT,这个是很明显的特征值分解形式 A T A V Σ…
数据封装与解封装过程
目录
前言
一、数据封装与解封装过程
1.1、数据封装过程
1. 2、数据解封装过程
1.3、相关数据传输的一些基本概念
1.3.1 PDU图示
1. 3.2 常见硬件设备与五层模型的对应关系
二、数据封装与解封装过程
总结 前言
我们在进行网络通信时,需要数据包在不同网…
【已解决】ModuleNotFoundError: No module named ‘PIL‘
问题描述 Traceback (most recent call last): File "train.py", line 75, in <module> import PILModuleNotFoundError: No module named PIL 解决办法 pip install pillow
深度学习笔记之线性代数
深度学习笔记之线性代数
一、向量
在数学表示法中,向量通常记为粗体小写的符号(例如,x,y,z)当向量表示数据集中的样本时,它们的值具有一定的现实意义。例如研究医院患者可能面临的心脏病发作风…
线性代数本质系列(一)向量,线性组合,线性相关,矩阵
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第一篇
向量究竟是什么? 向量的线性组合,基与线性相关 矩阵与线性相关 矩阵乘法与线性变换 三维空间中的线性变换 行列式 逆矩阵,列空间,秩与零空间 克莱姆…
矩阵论(Matrix)
大纲
矩阵微积分:多元微积分的一种特殊表达,尤其是在矩阵空间上进行讨论的时候逆矩阵(inverse matrix)矩阵分解:特征分解(Eigendecomposition),又称谱分解(Spectral decomposition…
机器学习中的数学知识2——雅可比矩阵与Hessian矩阵
4.雅可比矩阵
对于如下向量到向量的映射函数: yf(x)\mathbf yf(\mathbf x)yf(x) 其中,向量x∈Rn\mathbf x\in\mathbb R^nx∈Rn,向量y∈Rm\mathbf y\in\mathbb R^my∈Rm,这个映射分量形式为: yifi(x)y_{i}f_{i}(\mathbf x)yifi…
矩阵的其他性质及其运算技巧
1.单位矩阵(E):类似实数运算中的“1”,任何矩阵乘单位矩阵都等于该矩阵本身,但不同矩阵对应的单位矩阵不同。
2.矩阵乘法满足结合律和分配律,但不满足交换律,原因见三。
3.当两个不同阶矩阵相…
逆矩阵相关性质与例题
1.方阵的行列式:就是将方阵中的每一个元素转换至行列式中。 1.性质一:转置方阵的行列式等于转置前的行列式。(对标性质:行列式与它的转置行列式相等) 2.性质二:|ka||a|*k的n次方,n为方阵阶数。 …
人工智能教程(二):人工智能的历史以及再探矩阵
目录 前言
更多矩阵的知识
Pandas
矩阵的秩 前言 在上一章中,我们讨论了人工智能、机器学习、深度学习、数据科学等领域的关联和区别。我们还就整个系列将使用的编程语言、工具等做出了一些艰难的选择。最后,我们还介绍了一点矩阵的知识。在本文中&am…
SimSolid技术原理解析 衡祖仿真
面向超大规模结构的无网格分析软件Altair SimSolid,自从面世以来,受到广大工程师的关注。SimSolid 是面向设计师、工程师和分析师的颠覆性仿真技术,可在几分钟内对结构复杂的 CAD 装配体进行结构分析。它消除了传统结构仿真中非常耗时、非常专…
OpenGL课程设计 三维图形交互程序 bunny兔+飞机模型
链接: https://pan.baidu.com/s/1cBTTbbzRCVBCX_H4jf6qMA 提取码: kj8w 一、实验要求和内容 1.1 实验内容 (1)实验描述 实现一个三维图形交互程序,能够读入三维obj文件、绘制并打上光照,并且实现基本的三维交互—包含平移、旋转和缩放。要求能够成功读取…
迭代法 求解线性方程组
迭代法 求解线性方程组 (MATLAB) 统筹了 李庆扬《数值分析》第五版中关于求解Axb的四种常用迭代法 一码多用 Jacobi、Gauss-Seidel、SOR、SSOR四种迭代法 可以自行选择迭代方法,自定义精度,选择收敛判定方案 交互式软件般的体验
代码如下
c…
矩陣的跡(matrix trace)的特性以及證明
矩陣的跡(matrix trace)的特性以及證明前言definitionlinear mappingtrace of product性質一證明性質二證明cyclic property證明前言
本篇整理自深藍學院三維點雲處理課程的Lecture 9 – Registration,並補上證明。
definition tr(A)∑i1na…
Asia Hong Kong Regional Contest 2016(2021/10/6)
Asia Hong Kong Regional Contest 2016B Kattis doors题目分析与大意代码C Playing with Numbers题目大意及分析代码J Taboo题目大意及分析代码题目链接B Kattis doors
题目分析与大意
就是在两个球之间找能够通过的最大半径,其实就是求几次点到线段的距离。(直接…
Latex公式中矩阵的方括号和圆括号表示方法
一、背景
在使用Latex写论文时,不可避免的涉及到矩阵公式。有的期刊要求矩阵用方括号,有的期刊要求矩阵用圆括号。因此,特记录一下Latex源码在两种表示方法上的区别,以及数组和方程组的扩展。
二、矩阵的方括号表示
首先所有的…
线性代数入门与学习笔记
该内容为重拾部分线性代数知识的学习笔记,内容上更多的是为了解决问题而学习的内容,并非系统化的学习。 针对的问题为:Music算法推导求解过程中的矩阵计算知识。 学习的内容包括:矩阵原理、矩阵行列式、矩阵的秩、线性变换矩阵变换…
【考研数学】矩阵、向量与线性方程组解的关系梳理与讨论
文章目录 引言一、回顾二、梳理齐次线性方程组非齐次线性方程组 写在最后 引言
两个原因让我想写这篇文章,一是做矩阵题目的时候就发现这三货经常绑在一起,让人想去探寻其中奥秘;另一就是今天学了向量组的秩,让我想起来了之前遗留…
04 - 矩阵乘法与线性变换复合
回到目录
04 - 矩阵乘法与线性变换复合 为了更好的讲解矩阵*矩阵的思想。我们回到上一节的线性变换的两个普通的原则“保持直线”和“原点不变”。可以总结出2种变换的方式:旋转和剪切。 上面这个坐标基让我们先旋转 再剪切(剪切可能从字面上有些不好…
2020-10-05
解N元一次线性方程组
方程组形如: a11X1a12X2……a1nXnb1 a21X1a22X2……a2nXnb2 …… an1X1an2X2……annXnbn 解题思路: 1、一个N元一次方程组,可以通过求系数矩阵获得方程的解。 (1)计算所有a的系数矩阵值d…
计算一个点在某平面中某条直线的投影
假设点 PPP 在平面 π\piπ 上,而直线 LLL 在平面 π\piπ 上与另一条直线 DDD 相交。要计算点 PPP 在直线 LLL 上的投影 QQQ,可以按照以下步骤进行:
计算直线 DDD 的方向向量 d⃗\vec{d}d,例如取直线 DDD 上的两个点 AAA 和 BBB…
VINS-Mono-VIO初始化 (六:基于已知重力对重力方向进行调整)
可以通过查表的方式直到重力的大小,假设为9.81,我们取出重力的方向然后大小直接设置为9.81 这样调整的目的是因为,上一节求解的方程中的已知量中也是包含的重力的误差影响在里面的,需要这样对误差调整回来
论文中的图如下 我们就…
matlab_矩阵和数组
官方: MATLAB 是“matrix laboratory”的缩写形式。MATLAB 主要用于处理整个的矩阵和数组,而其他编程语言大多逐个处理数值。 所有 MATLAB 变量都是多维数组,与数据类型无关。矩阵是指通常用来进行线性代数运算的二维数组。 数组创建
要创建…
高斯消元法解异或线性方程组
高斯消元法
对于一组线性方程组,枚举每一列进行如下步骤: 1、找到首元非零行 2、将这一行交换到第一行 3、将这一行的第一个数变成1,对当前这一行进行操作,不涉及矩阵的初等变换 4、将下面所有行的当前列全部消成0,利…
排序不等式 GCJ 2008 Round1A Problem A. Minimum Scalar Product
排序不等式(Rearrangement Inequality)又称排序原理,是数学上的一种不等式。它可以推导出很多有名的不等式,例如:算术几何平均不等式、柯西不等式、切比雪夫总和不等式。 简洁的来说就是两组数对应“顺序”相乘的和 &g…
最小二乘法原理-线性回归
最小二乘法公式是一个数学的公式,在数学上称为曲线拟合,此处所讲最小二乘法,专指线性回归方程,最小二乘法公式为ay(平均)-b*x(平均)。
有一组数据(1,6),&…
线性代数Python计算:矩阵对角化
线性变换TTT的矩阵A∈Pnn\boldsymbol{A}\in P^{n\times n}A∈Pnn的对角化,即寻求对角阵Λ\boldsymbol{\Lambda}Λ,使得A\boldsymbol{A}A~Λ\boldsymbol{\Lambda}Λ,需分几步走: (1)解方程det(λI−A)0\det(\lambda\boldsymbol{I…
视觉SLAM14讲笔记02:ch5针孔,双目相机模型
相机
相机将三维世界中的坐标点(单位为米)映射到二维图像平面(单位为像素)的过程能够用一个几何模型进行描述。这个模型有很多种,其中最简单的称为针孔模型。针孔模型是很常用,而且有效的模型,…
深度学习数学基础1_函数与极限
一、极限的公理化定义
如果任意伊布舍隆,总是存在一个正数德尔塔,当0<|x-x0|<德尔塔时,总有|f(x)-A|<伊布舍隆,则
f(x)的极限为A。
线性代数mit18.06读课本-D1-1.1
一、preface
天下无敌第一可爱!
二、INTRODUCTION TO VECTORS
1.1向量加法&线性组合
1、引入向量 2、向量加法(vector addition) 3、数乘(scalar multiplication) 4、线性组合(linear combinat…
D3-AcWing-复习785-798
今天下午有课,学习算法时间被冲刷,上午先复习一下!!!
一、785
1、注意边界条件判断的问题,别忘了。 2、’ .join()输出的问题。
def quick_sort(q,l,r):if l>r:returni,j,x l-1,r1,q[lr>>1]wh…
线性代数矩阵转置乘法_矩阵的乘积及其转置属性 使用Python的线性代数
线性代数矩阵转置乘法Prerequisites: 先决条件: Defining a Matrix 定义矩阵 Transpose Matrix 转置矩阵 In linear algebra, an mxn matrix A is multiplied with its transpose AT then the resultant matrix is symmetric. This is one of the most common ways…
python scipy linalg.toeplitz
1、可以安装pip install toeplitz 2、scipy.linalg.toeplitz(c, rNone) 构造一个Toeplitz矩阵。
Toeplitz矩阵具有恒定的对角线,其中c为第一列,r为第一行。如果没有给出rr conjugate©假设。
参数: c:array_like 矩阵的第一…
用gauss消去法解线性方程组(数值数学实验教程P74ex5.2)-2021-11-03
用gauss消去法解线性方程组(数值数学实验教程P74ex5.2)
function [x,Ak] caguss_elimination(A,b,epsilon) %gauss消去法解线性方程组 %A-系数矩阵;b-右端向量 %输出Ak(:,:,k)三维数值,它的第k页保存消元过程中的第k次消元后得到…
unilm三种模型结构中mask矩阵的代码实现
UNILM全名Unified Language Model Pre-training for Natural Language Understanding and Generation。NU直接用BERT做,NLG直接把BERT的 S1 [SEP] S2 当成 encoder-decoder,虽然没有那个结构,但是心中有那个思想。 seq-to-seq LM中的mask矩阵…
元宇宙密室逃脱游戏攻略来啦!
今天还是数字人小杜如果有一款线上 PC 端游戏,不用安装下载,一秒登入,且在开头5分钟就甚至能撸出大致结局,你会去玩吗?今晚我在 Vland 元宇宙空间,体验语音版的密室逃脱。LetmeOut密室逃脱无界社区 Mixlab …
LeetCode50天刷题计划(Day 28— 螺旋矩阵(18.30-19.20)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、题目螺旋矩阵示例提示二、思路三、代码前言
我又肥来啦~之前消失了五天准备seu的夏令营面试 (解释一下嘻嘻) 以后继续!&…
推荐系统 理论笔记 二 (数学基础)
线性代数
微积分 梯度是一个向量,向量里的每一个值都是不同自变量(方向)的偏导数。 所以的偏导构成的向量,就是梯度。大小就是最快方向的变化值。
基于遗传算法(GA)工具箱优化求解一元函数优化 -【 附代码+详细注解】
基于遗传算法工具箱求解一元函数优化 -【 附代码详细注解】一.优化函数二.优化后的实际效果三.代码部分前言:链接:
遗传算法工具箱下载地址.链接:
遗传算法工具箱的导入MatLab软件教程地址.一.优化函数
此次是基于上次发表的的资源——遗传算法工具箱以及工具箱导…
【Matlab风电功率预测】麻雀算法优化LSSVM风电功率预测(多输入单输出)【含源码 1718期】
一、代码运行视频(哔哩哔哩)
【Matlab风电功率预测】麻雀算法优化LSSVM风电功率预测(多输入单输出)【含源码 1718期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]仝卫国,郭超宇,赵如意.基于改进麻雀算法优化…
线性代数(考前冲刺版)
线性代数_考前冲刺版1.行列式1.行列式1.n级排列2.行列式2.行列式的性质3.行列式按行展开4.行列式的计算5.克莱姆法则2.矩阵1.矩阵的概念2.矩阵的运算3.特殊矩阵(方阵)1.数量矩阵2.对角矩阵3.上三角形和下三角形矩阵4.对称矩阵和反对称矩阵4.逆矩阵1.方阵2.伴随矩阵3.逆矩阵4.矩…
【码极客精讲】二维数组
二维数组本质上是以数组作为数组元素的数组,即“数组的数组”,类型说明符 数组名[常量表达式][常量表达式]。二维数组又称为矩阵,行列数相等的矩阵称为方阵。对称矩阵a[i][j] a[j][i],对角矩阵:n阶方阵主对角线外都是…
PTA-矩阵A乘以B
给定两个矩阵A和B,要求你计算它们的乘积矩阵AB。需要注意的是,只有规模匹配的矩阵才可以相乘。即若A有Ra行、Ca列,B有Rb行、Cb列,则只有Ca与Rb相等时,两个矩阵才能相乘。
输入格式:
输入先后…
矩阵代数与MATLAB实现(特征值、广义特征值、酋矩阵、)
矩阵代数的相关知识 目录
一、特征值与特征向量
1、特征值与特征向量
2、MATLAB计算
二、广义特征值与广义特征向量
1、广义特征值与广义特征向量
2、MATLAB计算
三、酋矩阵
1、酋矩阵
2、MATLAB计算
四、未完待续 总结 提示:以下是本篇文章正文内容&…
绕任意轴旋转矩阵推导
该文是在学习 Physically Based Rendering 第2.7.6节绕任意轴旋转时对其公式的推导产生了兴趣。 首先,如图所示: 已知条件: 1). v\mathbf{v}v 是被旋转的向量。 2). a\mathbf{a}a 是围绕旋转的轴。 3). θ\thetaθ 是旋转的角度。
解决思路…
240. 搜索二维矩阵 II——剑指Offer
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性: 每行的元素从左到右升序排列。 每列的元素从上到下升序排列。 class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {…
MIT_线性代数笔记:第 07 讲 求解 Ax=0:主变量,特解
目录 前言计算零空间 Nullspace特解 Special solutions行最简阶梯矩阵 Reduced row echelon form (rref) 前言
我们定义了矩阵的列空间和零空间,那么如何求得这些子空间呢?本节课的内容即从定义转到算法。
计算零空间 Nullspace…
线性代数基础总结LAN
标量(scalar): 一个标量就是一个单独的数,它不同于线性代数中研究的其他大部分对象(通常是多个数的数组)。 向量(vector): 一个向量是一列数。这些数是有序排列的。通过次…
Halcon中从两组点的对应关系生成仿射矩阵,及思考原理和代码实现
有几个算子有点类似,看了下区别
1.vector_to_rigid( : : Px, Py, Qx, Qy : HomMat2D)
2.vector_to_similarity( : : Px, Py, Qx, Qy : HomMat2D)
3.vector_to_aniso( : : Px, Py, Qx, Qy : HomMat2D) vector_to_rigid 这个是刚性变换, 只有旋转和平移…
李群李代数求导-常用求导公式
参考
A micro Lie theory for state estimation in robotics manif issues 116
常用求导公式
Operation左雅克比右雅克比X−1\mathcal{X}^{-1}X−1JXX−1−I\mathbf{J}_{\mathcal{X}}^{\mathcal{X}^{-1}}\mathbf{-I}JXX−1−IJXX−1−AdX\mathbf{J}_{\mathcal{X}}^{\mathc…
计算机图形学笔记一:基础变换
基础变换1.变换的作用2.二维变换2.1缩放变换(Scale Transform)2.1.1等比例缩放2.1.2不等比例缩放2.2对称变换(Reflection Transform)2.3错切变换(Shear Transform)2.4旋转变换(Rotation Transfo…
矩阵处理—Zigzag矩阵打印
与其明天开始,不如现在行动! 文章目录 Zigzag矩阵打印1.1 题目描述1.2 解决思路1.3 代码实现 💎总结 Zigzag矩阵打印
1.1 题目描述
有一个n行m列的矩阵,要求按照Z字形打印出数据,如图: 1.2 解决思路
用一…
冯诺依曼(Von Neumann)迹不等式证明
文章目录冯诺依曼迹不等式的定义冯诺依曼迹不等式的证明柯西中值定理数学归纳法冯诺依曼迹不等式的证明冯诺依曼迹不等式的定义
假设A∈Sn\mathbf{A} \in {\mathbb{S}_{}^n}A∈Sn,B∈Sn\mathbf{B} \in {\mathbb{S}_{}^n}B∈Sn,其特征值分别为&#…
MATLAB+三对角矩阵
(对角线上元素相同的) 一、生成对角矩阵的基本用法 1、diag(a) 使用diag(a)命令生成对角矩阵,a为某个向量,如下所示:
2、diag(a,i) 使用diag(a,i)命令生成,a为某个向量,i为a向量相对主对角线偏…
以矩阵的形式,对点或线段或多边形绕固定点旋转方法
一、仅旋转
,其中x,y旋转前横纵坐标,x’,y’为旋转后横纵坐标。θ旋转角度,单位为弧度。
等价于:x’ xcosθysinθ,y’-xsinθycosθ
注:此矩阵仅为旋转矩阵,不包含平移和缩放。 二、旋转平…
【GNSS】RTKLIB 中 LAMBDA 搜索整周模糊度的算法实现
文章目录Part.I IntrodctionChap.I 预备知识Part.II 代码详解Chap.I lambdaChap.II LDChap.III reductionChap.IV searchPart.III 一个实例Chap.I 测试函数Chap.II 结果输出Chap.III 结果分析 & 验证ReferencePart.I Introdction
本篇博文的目的是:对RTKLIB中L…
任意分圆环下的 RLWE:如何产生正确的噪声分布
参考文献:
[Con09] Conrad K. The different ideal[J]. Expository papers/Lecture notes. Available at: http://www.math.uconn.edu/∼kconrad/blurbs/gradnumthy/different.pdf, 2009.[LPR10] Lyubashevsky V, Peikert C, Regev O. On ideal lattices and learn…
线性代数Python计算:对称矩阵的对角化
numpy.linalg包提供了函数 eigh(A)\text{eigh(A)}eigh(A) 计算并返回参数A表示的对称矩阵的特征值v和由特征向量经过标准正交化后构成正交矩阵P。其中返还的特征值数组v中元素按升序排列,P中的各列对应属于v中特征值的特征向量。 例1 用Python计算使得矩阵A(22−225…
线性代数Python计算:方阵的伴随阵
numpy的array对象是可以通过下标访问其某一片段的:长度为n的数组a,对0≤\leq≤i≤\leq≤j≤\leq≤n,a[i:j]表示片段 a[i],a[i1],⋯,a[j-1]\text{a[i],a[i1],$\cdots$,a[j…
csdn冷知识:如何在csdn里输入公式或矩阵
目录
1 输入公式
2 输入矩阵
3 如何输入复杂公式
4 如何修改,已经生成的公式 1 输入公式
进入编辑模式点击右边的菜单:公式然后进入公式编辑器,选择右边的 ... 可以选择大括号等,右边还有矩阵符号选择后你需要创建几行几列的…
程序员的自我修养之数学基础01:行列式(定义、意义、计算方法和伴随矩阵)
行列式的定义
行列式是由一些数据排列成的方阵经过规定的计算方法而得到的一个数,如果行列式中含有未知数,那么行列式就是一个多项式。
行列式本质上代表一个数值,这点请与矩阵区别开来。矩阵只是一个数表,行列式还要对这个数表…
线性代数的本质(笔记一)
注:本篇笔记来源于《线性代数的本质》一课程。
写在前面
本课程主要通过几何来了解线性代数
1. 向量
对于向量有三种观点:
物理学 具有大小和方向计算机 数组,列表数学 概括前面两者,只要保证向量的加法和数乘有意义即可。…
数学_计算协方差矩阵/信息矩阵_理论+例子
目录
1. 多元高斯分布
1.1 标准高斯分布
1.2 一元高斯函数(一元高斯分布概率密度) 1.3 多元高斯分布
2. 协方差矩阵的计算
2.1 问题定义
2.2 室内外温度的例子
参考: 1. 多元高斯分布
1.1 标准高斯分布
标准高斯函数(正态…
【算法 】两组随机变量协方差矩阵 矩阵的特征值与特征向量
协方差矩阵 矩阵的特征值与特征向量 算法程序下载:摘要1 项目介绍2 关于协方差矩阵维度2.1CCA算法2.2矩阵的特征计算 3数据获取4结果4.1代码 5结论 算法程序下载:
地址
摘要 对于两个矩阵x(5,10),y(10,10…
JWFD开源工作流-矩阵引擎设计-高维向量空间分析法
JWFD开源工作流-矩阵引擎设计-高维向量空间分析法 在把已知的流程节点查找到之后,输出下标,但是我们发现,还有一些节点并未被 探测到,遍历并没有完全的完成,仍然有泄露的节点在其中,这个问题…
GAMES101学习笔记(Lecture1-2)
该笔记基于闫令琪大神的GAMES101课程及课后作业总结而成 目录
学习过程中遇到的一些词
线代基础
Eigen库的用处
矩阵/向量的练习: 学习过程中遇到的一些词
Geometrically: Parallelogram law & Triangle law 几何:平行四边形定律和三角形定律
Alg…
矩阵求逆_伴随矩阵法
1、基本知识
首先展示一个nnn阶行列式: D∣a11a12…a1na21a22…a2n…………an1an2…ann∣a11A11a12A12⋯a1nA1nD\left|\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \ldots & \…
4.5 函数最佳逼近
学习目标:
要学习函数最佳逼近,我可能会采取以下几个步骤: 学习基本的数学知识和工具:函数最佳逼近涉及到线性代数、实变函数、泛函分析等多个领域的知识,因此我需要先学习这些基础知识和工具,例如矩阵和向…
【视觉SLAM十四讲学习笔记】第三讲——Eigen库
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵 本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动? Eigen…
位姿变换矩阵从Sophus库的SE3f类型转换为OpenCV库的Mat类型
cv::Mat Tcw;
Sophus::SE3f Tcw_SE3f = mpSLAM->TrackMonocular(cv_ptr->image,cv_ptr->header.stamp.toSec());
Eigen::Matrix4f Tcw_Matrix = Tcw_SE3f.
兩隨機變數乘積的期望值
兩隨機變數乘積的期望值以下推導參考Distribution of the product of two random variables - Expectation of product of random variables。 E(XY)E(E(XY∣Y))law of total expectationE(Y⋅E[X∣Y])外層給定Yy,所以Y對內層期望值來說為常數\begin{aligned} \opera…
第三章,矩阵,09-线性方程组解的判断与求法、矩阵方程
第三章,矩阵,09-线性方程组解的判断与求法、矩阵方程 定理推论1推论2推论3推论4 矩阵方程AXB解法解的存在性推论 玩转线性代数(21)线性方程组解的判断与求法的笔记,相关证明以及例子见原文 定理
对n元线性方程组 A x b Axb Axb,…
MATLAB中自带排序函数 ssort 排序消耗时间分析
题目:
用函数 random0random0random0 产生三个由随机数组的数组,三个数组分别包含100,1000,2000100,1000,2000100,1000,2000个元素。下一步,用函数 toctoctoc 和 tictic…
数值分析Guass分解——错误讨论
在数值分析求解线性方程组当中常常会用到高斯分解,对线性方程组的系数矩阵AAA进行 LLL、UUU分解, 即:AL∗UA L*UAL∗U 其中 LLL 为主对角线元素均为 1的单位下三角矩阵, UUU 为 上三角矩阵,可以将原线性方程组 AxbAxbAxb…
04 矩阵乘法与线性变换复合
矩阵乘法与线性变换复合 复合变换 这是关于3Blue1Brown
"线性代数的本质"的学习笔记。 复合变换 图1 复合变换 复合变换原则,依次变换,即先变换的矩阵乘待变换的向量后,得到的结果,再用后变换的矩阵乘此结果向量。从矩…
线性代数的本质(三)——线性方程组
文章目录 线性方程组高斯消元法初等行变换线性方程组的解向量方程齐次线性方程组的解非齐次线性方程组的解 线性方程组
高斯消元法
客观世界最简单的数量关系是均匀变化的关系。在均匀变化问题中,列出的方程组是一次方程组,我们称之为线性方程组(Linea…
LaTex语法实现多种矩阵
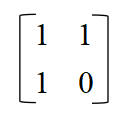
矩阵 0 1 1 0 \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} 0110
\begin{matrix}0 & 1 \\1 & 0
\end{matrix}小括号矩阵 ( 0 1 1 0 ) \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} (0110)
\begin{pmatrix}0 & 1 \\1 & 0
\end{pm…
【Matlab】如何将二阶线性微分方程进行Laplace变换得到传递函数
二阶线性微分方程进行Laplace变换 前言正文代码实现 前言
二阶线性微分方程: 一个二阶线性微分方程通常可以写成如下形式: y ′ ′ ( t ) p ( t ) y ′ ( t ) q ( t ) y ( t ) f ( t ) y^{\prime \prime}(t)p(t) y^{\prime}(t)q(t) y(t)f(t) y′′(t)p(t)y′(t)q(t)y(t)f(…
2维旋转矩阵的推导方式
1、向量空间推导
先复习向量空间的定义
向量空间的定义是:设V为n维向量的集合,若集合V非空,且集合V对于向量的加法及数乘两个运算封闭,那么称集合V为向量空间。
也就是说向量空间集合运算运算对集合封闭,三个要素满…
线性代数Python计算:线性方程组的通解
对齐次线性方程组 {a11x1a12x2⋯a1nxn0a21x1a22x2⋯a2nxn0⋯⋯⋯am1x1am2x2⋯amnxn0(1)\begin{cases}a_{11}x_1a_{12}x_2\cdotsa_{1n}x_n0\\a_{21}x_1a_{22}x_2\cdotsa_{2n}x_n0\\\quad\quad\quad\cdots\quad\cdots\quad\cdots\quad\\a_{m1}x_1a_{m2}x_2\cdotsa_{mn}x_n0\end{c…
mathematica线性代数基础和希腊字母输入
在公式推导的过程中最常使用的就是线性代数:
mathematica提供了线性代数的计算模块,不过需要熟悉一下语法,最好的方式就是看文档。
文档的链接
在本地的帮助搜索栏输入howto/DoLinearAlgebra,或者在网页输入链接 How to| 进行线…
c++实现n阶行列式计算
思路简述: 将n阶行列式化为上三角行列式,对角元乘积之和即为行列式的值。
#include "iostream"
using namespace std;
void main ()
{double a[10][10]{0},result1;//10阶以上行列式要对a数组修改大小int i,j,k,t;int size;cout<<"…
线性代数高级--矩阵的秩--SVD分解定义--SVD分解的应用
目录
矩阵的秩
概念
k阶子式
矩阵的秩的定义
矩阵的秩的性质
SVD分解
概念
注意
SVD的分解过程
SVD分解的应用 矩阵的秩
概念
矩阵的秩是线性代数中的一个重要概念,用于描述矩阵的行(或列)向量的线性无关程度。矩阵的秩可以通过…
【Matlab单目标优化求解】非线性权重的自适应鲸鱼算法求解单目标优化问题(NWAWOA)【含源码 1665期】】
一、代码运行视频(哔哩哔哩)
【Matlab单目标优化求解】非线性权重的自适应鲸鱼算法求解单目标优化问题(NWAWOA)【含源码 1665期】】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]欧名勇,陈仲伟,谭玉东,文明,周志成.基于峰谷分时电价…
一文彻底搞懂积分等式证明题(积分证明题总结笔记1/3)
积分证明题是考研中难度较大的板块,很多学弟学妹们希望我出一篇总结文章,故作本文,希望对大家有所帮助。 本文所涉及题目,均是来自市面上常见题册(李林880,张宇1000题,汤家凤1800等)…
证明正定矩阵的充要条件:全部顺序主子式大于0
定理: f x T A x f x^TAx fxTAx 正定的充要条件是 A A A 的全部顺序主子式大于零。
必要性:即 f x T A x f x^TAx fxTAx 正定 ⇒ \Rightarrow ⇒ A A A 的全部顺序主子式大于零。
首先,由于 f x T A x f x^TAx fxTAx 正定&…
为什么初等矩阵左乘相当于行变换,右乘相当于列变换
初等矩阵左乘一个矩阵A,是用初等矩阵的行乘矩阵A的列,是对矩阵A的行之间的倍乘、互换、倍加,相当于矩阵A的行变换。 右乘一个矩阵A,是用初等矩阵的列乘矩阵A的行,是对矩阵A的列之间的倍乘、互换、倍加,相当…
数据包络分析(DEA)——CCR模型
写在前面: 博主本人大学期间参加数学建模竞赛十多余次,获奖等级均在二等奖以上。为了让更多学生在数学建模这条路上少走弯路,故将数学建模常用数学模型算法汇聚于此专栏,希望能够对要参加数学建模比赛的同学们有所帮助。 目录 1. …
线性代数 第五章 特征值与特征向量
一、特征值定义 二、特征值求法
定义法;;相似。
三、特征向量求法
定义法;基础解系法;;相似。
四、特征值性质
不同特征值的特征向量线性无关k重特征值至多有k个线性无关的特征向量
五、相似的定义
若ÿ…
【MVP矩阵】投影矩阵推导与实现
投影矩阵推导
参照games101课程,这里只列举一些信息备忘。 正交投影推导结果如下
透视投影推导结果如下
备注
一般情况下,透视投影我们使用的是下面的矩阵,因为视锥体的r、l、t、b信息一般不好拿到 这个第三行三列和三行四列和上面一样…
【已解决】AttributeError: module ‘gradio‘ has no attribute ‘Image‘
问题描述 AttributeError: module gradio has no attribute Image 不知道作者用的是哪个gradio版本,最新的版本报错AttributeError: module gradio has no attribute outputs , 换一个老一点的版本会报错AttributeError: module gradio has no attribute…
【课堂笔记】线性规划(方述诚)L1L2 介绍和预备知识
记录线性规划的笔记,学习过程难免出错,欢迎指出错误。 课程为方述诚教授线性规划公开课,文中图片为课程PDF中截取,版权归PDF所有者。 文章目录L1 Introduction线性规划(LP)历史大规模线性规划问题的求解思路L2 求解前的准备工作LP…
面试题12:矩阵中的路径
面试题12:矩阵中的路径
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“…
第七章,相似矩阵及其应用,3-二次型、合同矩阵与合同变换
第七章,相似矩阵及其应用,3-二次型、合同矩阵与合同变换 二次型相关概念二次型二次型的标准形和规范形表示形式 合同矩阵与合同变换定义 合同合同矩阵的性质等价、相似、合同三种关系的对比等价相似合同 玩转线性代数(38)二次型概念、合同矩阵与合同变换…
02 栈的原理与使用
💖💖感谢各位观看这篇文章,💖💖点赞💖💖、收藏💖💖、你的支持是我前进的动力!💖💖 💖💖感谢你的阅读💖,专栏文章💖持续更新!💖关注不迷路!!💖 01 线性表的原理与使用 文章目录 什么是堆栈后缀表达式栈的抽象数据类型描述栈的顺序存储实现…
函数的求导法则——“高等数学”
今天,小雅兰的内容是函数的求导法则,上篇博客我们知道了导数的定义、导数的几何意义及可导与连续关系,这篇博客我们来仔细学习一下求导法则,下面,就让我们进入导数的世界吧 一、函数的和、差、积、商的求导法则 二、反…
2022高等代数笔记整理
2022高等代数笔记-b站宋浩基本内容笔记基本内容
01.二阶行列式 02.三阶行列式 03.排列与逆序 04.奇排列和偶排列 05.对换 06.n阶行列式 07.特殊行列式 08.行列式的性质 09.余子式 10.代数余子式 11.行列式按某一行(列)展开 12.行列式按一行展开 13.异乘变零定理 14.拉普拉斯定…
第五章 opengl之摄像机
OpenGL摄像机摄像机/观察空间Look At矩阵自由移动移动速度视角移动欧拉角鼠标输入缩放补充:摄像机类摄像机
OpenGL本身没有摄像机(Camera)的概念,但我们可以通过把场景中的所有物体往相反方向移动的方式来模拟出摄像机,产生一种我们在移动的…
LA@determinant@行列式@Vandermonde行列式
文章目录determinant行列式Vandermonde行列式行列式定义(公式)行列式性质🎈二阶行列式对角线法三阶行列式对角线法降阶展开法转置行列式转置范德蒙行列式拓展形式determinant行列式Vandermonde行列式
行列式定义(公式) n阶行列式∣A∣等于所有取自:不同行且不同列的…
动力学普遍定律的推导
假设质点系中第i个质点的质量为mi;作用在其上的有主动力Fi,约束力Fni,质点的惯性力为FIi。
应用达朗贝尔原理,单个质点的主动力,约束力和惯性力的矢量和为0.
两边同时乘以虚位移 deta r(i)
利用虚位移原理ÿ…
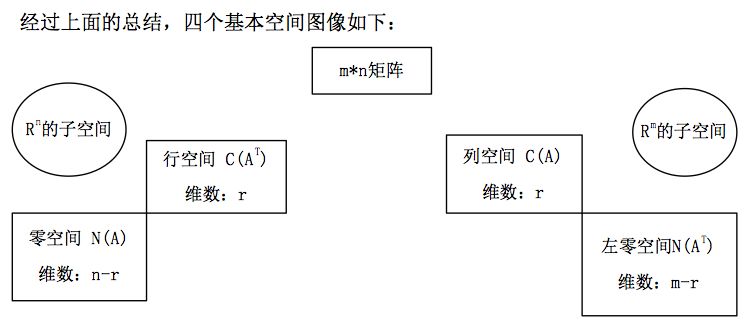
10 MIT线性代数-四个基本子空间 four fundamental subspaces
1. 四个子空间 Four subspaces (mxn)
列空间 Column space C(A) in
零空间Nullspace N(A) in
行空间Row space all combs of rows all combs of columns of AT C(AT) in
左零空间Left nullspace Nullspace of AT N(AT) left nullspace of A in 2. 基和维数 Basis&…
【人工智能里的数学】线性代数基础
系列文章目录
【人工智能学习笔记】人工智能里的数学——概述 【人工智能里的数学】一元函数微分学 文章目录系列文章目录前言一、向量与其运算1.2 行向量和列向量1.3 向量的运算1.3.1 向量的加减1.3.2 向量的数乘运算1.3.3 转置1.3.4 运算法则1.3.5 向量的内积1.4 向量的范数…
计算方法 5.线性方程组的解法(3)
线性方程组的迭代解法: 第一种迭代法: 专业的写法: 写成矩阵: 注意一下这里的LDU和之前的不是一个意思。 每次计算都用上一个矩阵,但是现有的矩阵已经有一些已经算好了: x数据实时更新。 用矩阵怎么表示呢&…
【数学】3b1b线性代数的本质——线性变换视角下的线性代数
文章目录1、如何理解线性代数?2、向量与线性变换3、矩阵与线性变换4、行列式与线性变换5、应用——逆矩阵求解线性方程组6、向量运算(点积,叉积,基变换)与线性变换7、特征向量与特征值8、多项式与抽象向量空间(二次型…
最大似然估计法和Zero Forcing算法的思考
文章目录一、Zero Forcing 算法思想二、MMSE三、MIMO检测中 Zero Forcing 算法比 Maximum Likelihood 差的思考本篇文章是学习了B站UP主
乐吧的数学 之后的笔记总结,老师讲的非常好,大家有兴趣的可以关注一波!一、Zero Forcing 算法思想
那…
几何的显式表示 - 曲线和曲面
点云:list of points(x, y, z) 将点云变成多边形的面,从而在计算机中输出多边形网格:Polygon Mesh 就是 拆成小三角 贝塞尔曲线 定义曲线只要满足起止点即可,P1,P2决定了它要往哪个方向弯 de Ca…
6.1 欧拉方法与改进欧拉方法
6.1.1 欧拉方法
欧拉方法是一种数值解常微分方程(ODE)的方法,可以用于近似求解给定的初值问题。它是以欧拉命名的瑞士数学家莱昂哈德欧拉所发明的,因此得名。
欧拉方法的基本思路是将连续的常微分方程转化为离散的形式。具体而言…
洛谷B2099 矩阵交换行
矩阵交换行
题目描述
给定一个 5 5 5 \times 5 55 的矩阵(数学上,一个 r c r \times c rc 的矩阵是一个由 r r r 行 c c c 列元素排列成的矩形阵列),将第 n n n 行和第 m m m 行交换,输出交换后的结果。
输入格式
输入共 6 6 6 …
快速入门matlab——单元数组
matlab中数组和矩阵的区别
基于matlab满天星制作
matlab中有关数组的基础知识
学习目标:深入掌握单元数组的各种使用方法
单元数组的一般建立方法
clear all;
c{大仙,daxian;[5 4 7 8 3],7} %两行两列,每个元素都可以类型不一样
c{1,1}
c{2,1…
【PTA题目】7-3 找鞍点 (20 分)
一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。
本题要求编写程序,求一个给定的n阶方阵的鞍点。
输入格式:
输入第一行给出一个正整数n(1≤n≤6)。随后n行,每行给出n个整数,其…
VINS预积分推导2
协方差矩阵传播
由式子可以看出,预积分噪声是IMU高斯白噪声的线性组合,因此预积分噪声也满足零均值的高斯分布: η i j [ δ ϕ i j δ v i j δ p i j ] N ˜ ( 0 9 1 , Σ i j ) {\eta _{ij}} \left[ \begin{array}{l}\delta {\phi _{…
抖音seo矩阵系统源码开发部署思路
抖音SEO矩阵系统源码开发和部署是一项复杂而又关键的任务。在开发阶段,我们需要根据抖音的搜索规则和算法,结合用户搜索意图和关键词,进行深入的研究和分析,以建立一个优秀的SEO矩阵系统。
在部署方面,我们需要遵循以…
矩阵-建模的应用思路碎片
目录
1.应用场景一:描述实体关系
1.1将文字描述的问题图形化看是否可用进一步抽象
1.2转换为表格
1.3将关系数字化
1.4 试探寻找可用直接解释的数学模型
1.5 如果不能寻找到,那么需要构建模型
2.应用场景二:描述组合关系
3.抽象方法…
机器学习-线性代数-向量、基底及向量空间
概述 文章目录 概述向量理解向量运算 基底与向量的坐标表示基底与向量的深入基底与向量选取与表示基底的特殊性张成空间 向量
理解 直观理解 行向量:把数字排成一行A [ 4 5 ] [4~ 5] [4 5]列向量:把数字排成一列A [ 4 5 ] \ \left [ \begin{matrix}…
C#,码海拾贝(15)——“对称正定矩阵”的求逆和“托伯利兹矩阵”求逆的“埃兰特”方法之C#源代码,《C#数值计算算法编程》源代码升级改进版
对称正定矩阵
在线性代数中,正定矩阵的性质类似复数中的正实数。与正定矩阵相对应的线性算子是对称正定双线性形式。
正定矩阵的行列式恒为正;实对称矩阵A正定当且仅当A与单位矩阵合同;若A是正定矩阵,则A的逆矩阵也是正定矩阵&a…
MATLAB二维绘图练习(一)
MATLAB二维绘图(一)使用plot函数进行简单绘图
1,颜色和线条: b blue 蓝 . point - solidg green 绿 o circle : dottedr red 红 x x-mark -. dashdot c …
[C++/PTA] 矩阵的乘法运算
[C/PTA] 矩阵的乘法运算 题目要求解题思路代码总结 题目要求
线性代数中的矩阵可以表示为一个row*column的二维数组,当row和column均为1时,退化为一个数,当row为1时,为一个行向量,当column为1时࿰…
机器学习 | SVD奇异值分解
本文整理自哔哩哔哩视频:什么是奇异值分解SVD–SVD如何分解时空矩阵 📚奇异值分解是什么? M是原始矩阵,它可以是任意的矩阵,奇异值分解就是将它分解为三个矩阵相乘。U和V是方阵,∑是不规则矩阵,…
短视频矩阵源码如何做应用编程?
短视频矩阵源码,
短视频矩阵系统技术文档:
可以采用电子文档或者纸质文档的形式交付,具体取决于需求方的要求。电子文档可以通过电子邮件、远程指导交付云存储等方式进行传输、
短视频矩阵{seo}源码是指将抖音平台上的视频资源进行筛选、排…
【深度学习】0-1 深度学习相关数学概念的简单总结-线性代数
线性代数
标量(scalar) 标量就是一个单独的数,只具有数值大小,而没有方向,部分有正负之分。一般用小写的变量名称表示,如a、x等。
向量(vector) 一个向量就是一列数,这…
(六)学习笔记:动手学深度学习(自动求导)
自动求导1.链式法则1.1向量的链式法则1.1.1实例一1.1.2实例二2.计算图3.自动求导的两种模式3.1正向累积和反向累积3.2反向累积总结3.3复杂度3.3.1反向累积和正向累积复杂度的对比4.自动微分4.1一个简单的例子4.2 非标量变量的反向传播4.3 分离计算4.4 Python控制流的梯度计算4.…
GAMES101笔记 Lecture03 Transformation
目录 Transoformation(变换)Why stuty transformation(为什么要学习变换呢?)2D transformations(2D变换)Scale transformation(缩放变换)Reflection Matrix(反射矩阵)Shear Matrix(切变矩阵) Rotate transformation(旋转变换)Linear Transforms Matrices(线性变换 矩阵) Hom…
CUDA编程模型系列三(矩阵乘)
CUDA编程模型系列三(矩阵乘)
本系列教程将介绍具体的CUDA编程代码的细节 CUDA编程模型系列三(矩阵乘) #include <stdio.h>
#include <math.h>#define BLOCK_SIZE 32
// error type & event
// a[][] * b[][] c[][]
// // b00 b01 b0…
(四)学习笔记:动手学深度学习(线性代数)
在这篇文章中我们将介绍线性代数中的基本数学对象、算术和运算,并用数学符号和相应的代码实现来表示它们。 线性代数1.1标量1.2向量1.2.1长度、维度和形状1.3矩阵1.3.1通过指定两个分量mmm和nnn来创建一个形状为mnm \times nmn的矩阵1.3.2 矩阵的转置1.4 张量1.5张量…
[数学建模]主成分分析法PCA
最常用的线性降维方法,通过某种线性投影,将高维的数据映射到低维的空间中,并期望在所投影的维度上数据的信息量最大(方差最大),以此使用较少的数据维度,同时保留住较多的原数据点的特性。 Q1:为…
6.14 Rayleigh商
定义 矩阵在某个向量处的瑞利商Rayleigh quotient是这样定义的: ρ(x):xHAxxHx\rho(x) :\frac{x^HAx}{x^Hx} ρ(x):xHxxHAx 这个怎么理解呢?上面是埃尔米特内积的表达式,下面是标准埃尔米特内积。但是矩阵不一定是对称阵,如果不是复数的话&#x…
偏微分方程简明教程第五章部分答案(2)
偏微分方程简明教程答案 第五章 抛物型方程习题5.25.2.15.2.25.2.55.2.65.2.85.2.9第五章 抛物型方程
习题5.2
5.2.1
1、设 L u = u t − u x x &#
有限元(FEM)基本知识速阅
一、有限元理论基础
1 什么是有限元 2. 固体力学的偏微分方程 密度 位移
3.本构方程 由弹性模型和泊松比就能确定 本构矩阵 进而确定应力和应变的关系 将含有9各变量的微分方程 变为 u v w 三个待求函数的 微分方程
需要进一步加入边界条件 才能求微分方程
4.边界条件 5.CA…
考研复试——线性代数(2)
文章目录线性代数面试问题:1. 什么是矩阵的秩?如何计算一个矩阵的秩?2. 什么是特征值和特征向量?如何计算矩阵的特征值和特征向量?3. 什么是正交矩阵?如何判断一个矩阵是否为正交矩阵?4. 什么是…
D - 统计子矩阵 (双指针+前缀和+降维处理)
D - 统计子矩阵 (双指针前缀和降维处理)
1、问题
D - 统计子矩阵
2、分析 代码
(1)纯暴力做法:
这个做法就很简单了,我们直接枚举所有的子矩阵,然后在对每一个子矩阵内部的元素逐一累加起…
抖音账号矩阵系统搭建
抖音账号矩阵系统搭建是指在抖音上建立一个多账号管理系统,包括多个账号的管理、运营、内容制作等方面的支持。具体搭建步骤如下:
1. 开通多个抖音账号,并将它们归纳为一个账号矩阵系统。
2. 建立一个统一的账号管理平台,以便对…
MIT线性代数笔记-第27讲-复数矩阵,快速傅里叶变换
目录 27.复数矩阵,快速傅里叶变换打赏 27.复数矩阵,快速傅里叶变换
对于实矩阵而言,特征值为复数时,特征向量一定为复向量,由此引入对复向量的学习 求模长及内积 假定一个复向量 z ⃗ [ z 1 z 2 ⋮ z n ] \vec{z} \…
x^Tx對x微分公式證明
x^Tx對x微分公式證明前言證明前言
本公式來自The Matrix Cookbook中的公式(131)。 證明 ∂xTx∂x∂(∑ixi2)∂x[∂(∑ixi2)∂x1∂(∑ixi2)∂x2...∂(∑ixi2)∂xn]T[∂x12∂x1∂x22∂x2...∂xn2∂xn]T2[x1x2...xn]T2x\begin{aligned}\frac{\partial x^Tx}{\partial x} & \f…
PCL - MLS代碼研讀(七)- 曲面擬合函數
PCL - MLS代碼研讀(七)- 曲面擬合函數computeMLSSurface宣告兩個變數計算鄰域內所有點的重心計算平面參數model_coefficients被投影點query_point檢查eigen_vector合理性計算局部坐標系原點計算曲率計算局部坐標系的三個軸向設定三個變數權重函數宣告四個…
相機內參矩陣K及其反矩陣推導與mve代碼研讀
相機內參矩陣K及其反矩陣推導與mve代碼研讀前言Kfill_calibrationK−1K^{-1}K−1fill_inverse_calibration前言
相機內參KKK將歸一化像平面上的點轉為圖像座標系上的點。
本篇由KKK推導出K−1K^{-1}K−1並與simonfuhrmann/mve裡的代碼做對照。
K
將世界座標系下歸一化像平面…
递归求解双递推摆动数列
已知递推数列:a(1)1,a(2i)a(i)1,a(2i1)a(i)a(i1),(i为正整数),试建立递归,求该数列的第n项与前n项的和。
思路:首先确立递归关系,当i为偶数时,递归关系是sum(n/2)1。当i…
GAMES101学习笔记(Lecture5以及对作业1的理解)
视口变换 作业1 基础版
模型变换:get_model_matrix(float rotation_angle)
//视图转换
Eigen::Matrix4f get_view_matrix(Eigen::Vector3f eye_pos)
{// 定义 4 * 4 的单位矩阵Eigen::Matrix4f view Eigen::Matrix4f::Identity();Eigen::Matrix4f translate;// 初…
利用SVD求得两个对应点集合的旋转矩阵R和转移矩阵t的数学推导
1.问题描述
给定两个在d维空间中对应的点集合P{p1,p2,…,pn}P \{ p_1,p_2 ,\dots , p_n\}P{p1,p2,…,pn}和Q{q1,q2,…,qn}Q \{ q_1 ,q_2, \dots , q_n \}Q{q1,q2,…,qn},为了计算出它们之间的刚体变换,即 RRR 和ttt,可以将其建模为如下的…
《程序设计基础》 第七章 数组 7-18 矩阵运算 (20 分)
给定一个nn的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。副对角线为从矩阵的右上角至左下角的连线。
输入格式:
输入第一行给出正整数n(1<n≤10);随后n行,每行给出n个整数&#…
《程序设计基础》 第七章 数组 7-13 判断上三角矩阵 (15 分)
上三角矩阵指主对角线以下的元素都为0的矩阵;主对角线为从矩阵的左上角至右下角的连线。
本题要求编写程序,判断一个给定的方阵是否上三角矩阵。
输入格式:
输入第一行给出一个正整数T,为待测矩阵的个数。接下来给出T个矩阵的信…
形式语言与自动机 图灵机
图灵机定义: 形式化定义: 转移函数显然要有下个状态,改写内容和向左向右。 一个经典的例子: 思路有了,怎么做呢?: 类似例子: 图灵机的表示能力: 举个例子: 那…
《程序设计基础》 第七章 数组 7-11 求矩阵各行元素之和 (15 分)
本题要求编写程序,求一个给定的mn矩阵各行元素之和。
输入格式:
输入第一行给出两个正整数m和n(1≤m,n≤6)。随后m行,每行给出n个整数,其间
以空格分隔。
输出格式:
每行输出对应矩阵行元素…
【PTA题目】7-8 求矩阵的局部极大值 (15 分)
给定M行N列的整数矩阵A,如果A的非边界元素A[i][j]大于相邻的上下左右4个元素,那么就称元素A[i][j]是矩阵的局部极大值。本题要求给定矩阵的全部局部极大值及其所在的位置。
输入格式:
输入在第一行中给出矩阵A的行数M和列数N(3≤…
【PTA题目】7-5 矩阵运算 (20 分)
给定一个nn的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。副对角线为从矩阵的右上角至左下角的连线。
输入格式:
输入第一行给出正整数n(1<n≤10);随后n行,每行给出n个整数&#…
(五)carla中世界坐标系与相机坐标系、像素坐标系变换
(五)carla中世界坐标系与相机坐标系、像素坐标系变换
由于实验需要将 carlacarlacarla 中世界坐标系下的坐标点画到相机采集的前视图上,故需要进行坐标系之间的转换。
转换中遇到的问题
参考这篇博客中给出的方法: link 发现将世界坐标系转…
面向对象的软件构造实验 1
需要记笔记的部分主要是UML类图知识。 这个插件可以帮助我们完成大多数工作。具体是这样使用这个插件的: 这样子把你的类全都写进去,他就会帮你画出类图。 不要指望傻瓜式操作,还是要自己写的。
这里注意一下:新增的变量和方法前…
计算机图形学笔记三:三角形光栅化
光栅化1.光栅化简析2.三角形光栅化1.光栅化简析
光栅化是将几何数据经过一系列变换后最终转换为像素,从而呈现在显示设备屏幕上的过程。 光栅化把东西画在屏幕上光栅化把东西画在屏幕上光栅化把东西画在屏幕上 而什么是屏幕? 屏幕有一个个像素点组成的…
线性代数的本质(笔记二)
行列式
理解矩阵的行列式其实就是理解线性变换对“体积”的影响。 (在二维里,就是指面积变化前后的缩放比例;那么三维里就是体积变化前后的缩放比例。)
以三维为例:
当行列式的值>1时,就是体积被放大…
MATLAB期末复习内容
第一章 MATLAB操作界面组成:MTALAB主窗口,命令行窗口,当前文件窗口,工作区窗口,命令历史记录窗口。 MATLAB提供了几种帮助 help用来查找函数用法 续行符: … 注释:% roots:解方程/ 帮助窗口&…
利用正弦定理证明两角和差公式
首先用正弦定理,证明sin(AB)sinAcosBcosAsinB。 另外,其它的两角和差公式,都可以用三角函数奇偶性、诱导公式等推导出来,无需再用正弦定理证明一遍。
PyTorch之Tensor的线性代数
PyTorch之Tensor的线性代数 trace() 对角线元素之和(矩阵的迹) import torch
# input
x torch.rand(3, 3)
x.trace()
# output
print(x)
tensor([[0.0441, 0.0921, 0.9778],[0.3825, 0.9165, 0.9853],[0.9345, 0.9116, 0.8807]])
print(x.trace())
tens…
矩阵乘法的计算复杂度
结论: A∗B(i,m)∗(m,j)A*B(i, m)*(m, j)A∗B(i,m)∗(m,j)的计算复杂度为O(i∗j∗m)O(i*j*m)O(i∗j∗m) 怎么来的:
输出矩阵C为(i,j)(i, j)(i,j),遍历输出矩阵,C矩阵中的每个元素由A,B矩阵中对应的m对数字相乘相加而来…
07自动求导(李沐深度学习笔记)
这里求导可以参看上一节这张图,∂<x,w>∂wxT∂w∂wwT∂x∂wxT∂w∂wxT\frac {\partial <x,w>}{\partial w}x^T\frac{\partial w}{\partial w}w^T\frac{\partial x}{\partial w}x^T\frac{\partial w}{\partial w}x^T∂w∂<x,w>xT∂w∂wwT∂w∂…
OpenGL 学习实录5: 基础光照 材质
OpenGL 学习实录5: 基础光照 & 材质 文章目录OpenGL 学习实录5: 基础光照 & 材质系列文章正文1. 光照场景2. 基础光照3. 加上材质其他资源参考连接完整代码示例系列文章
OpenGL 学习实录1: 基于 MacOS Clion 配置 OpenGL 运行环境OpenGL 学习实录2: 基础绘制初试Open…
分数的乘法公式是什么
分数的乘法公式是: (a/b) * (c/d) (a * c) / (b * d) 其中,a, b, c, d 是整数。 例如,(2/3) * (4/5) (2 * 4) / (3 * 5) 8/15。 注意,分数的乘法公式与整数的乘法公式不同,整数的乘法公式是: a * b c 其…
关于旋转矩阵的算法应用
date: 2021-11-22 15:59:18
一个nice的转换器
3D Rotation Converter
维基百科 Euler angles [超详细 有你想知道的一切]
关于图像旋转
详解 图像旋转变换 原理
三维坐标系旋转——旋转矩阵到旋转角之间的换算
欧拉角和旋转矩阵之间的转换 -知乎
四元数与欧拉角&#x…
【算法竞赛模板】求解线性方程组是否有解(求解矩阵的秩)
在实际运用中需判断线性方程组有无解,可以通过矩阵运算判断线性方程组是否有解 线性方程组有无解总结: 矩阵求解秩流程: 所以:当我们遇到题目问线性方程组是否有解时,只需求解系数矩阵的秩与增广矩阵的秩的关系 …
【Matlab扩频通信】扩频通信系统仿真(带面板)【含GUI源码 1587期】
一、代码运行视频(哔哩哔哩)
【Matlab扩频通信】扩频通信系统仿真(带面板)【含GUI源码 1587期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]王俊平,陈庆东,纪延俊.基于MATLAB的扩频通信系统的研究[J].科技展…
【转载】线性代数的本质笔记
1. 线性代数的两种认知
数值层面,这是大部分课程中的教学内容,能解决计算、应用问题。但却不是最本质的内容,它是在给定法则下的运算。几何层面。这个角度的线性代数可能更为接近本质,能帮助我们更好的认识线性代数这个工具&…
线性代数行列式的几何含义
行列式可以看做是一系列列向量的排列,并且每个列向量的分量可以理解为其对应标准正交基下的坐标。
行列式有非常直观的几何意义,例如:
二维行列式按列向量排列依次是 a \mathbf{a} a和 b \mathbf{b} b,可以表示 a \mathbf{a} a和…
《机器学习线性代数基础:Python语言描述》读书笔记----变换基底时的坐标换算
同一个向量在不同基底下的坐标计算。
坐标的表示是基于基底的
先来个简单的例子:在默认基底(a[1,0]T,b[0,1]T(a[1,0]^T,b[0,1]^T(a[1,0]T,b[0,1]T下,有向量u[3,3]Tu[3,3]^Tu[3,3]T,u的完整表达其实为 u3a3b3[10]3[01][3∗13∗03∗03∗1][33…
《机器学习线性代数基础:Python语言描述》读书笔记----逆矩阵
逆矩阵
设A是一个n阶矩阵,若存在另一个n阶矩阵B,使得: ABBAE ,则称方阵A可逆,并称方阵B是A的逆矩阵。
逆矩阵的存在性
不是每一个矩阵都存在逆矩阵的。因为矩阵的本质是映射,如果在映射过程中矩阵A压缩了…
《机器学习线性代数基础:Python语言描述》读书笔记----矩阵与向量
矩阵与向量
矩阵
由 m n 个数aija_{ij}aij排成的m行n列的数表称为m行n列的矩阵,简称m n矩阵。
可以看作是n个m维列向量从左到右并排摆放;行向量视角同理。
矩阵与向量
向量可以看作是一维矩阵:n维的列向量可以看作是一个n1的矩阵。 …
【Matlab TWVRP】遗传和粒子群算法求解带时间窗的车辆路径规划问题【含源码 1037期】
一、代码运行视频(哔哩哔哩)
【Matlab TWVRP】遗传和粒子群算法求解带时间窗的车辆路径规划问题【含源码 1037期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版&a…
【Matlab MTSP】灰狼算法求解多旅行商问题(同始终点)【含源码 1564期】
一、代码运行视频(哔哩哔哩)
【Matlab MTSP】灰狼算法求解多旅行商问题(同始终点)【含源码 1564期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]高珊,孟亮.贪婪随机自适应灰狼优化算法求解TSP问题[J]. 现代…
抖音SEO矩阵源码开发(一)
前言:
1.抖音SEO矩阵系统源码开发 是一项技术密集型工作,需要对大数据处理、人工智能等领域有深入了解。该系统开发过程中需要用到多种编程语言在服务器上安装LNMP环境,包括Linux操作系统、Nginx、MySQL、PHP等,如Java、Python等…
【Matlab路径规划】蚁群优化遗传算法求解机器人栅格地图最短路径规划问题【含源码 1581期】
一、代码运行视频(哔哩哔哩)
【Matlab路径规划】蚁群优化遗传算法求解机器人栅格地图最短路径规划问题【含源码 1581期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]刘传领.改进的蚁群遗传优化算法及其应用[J]. 计算机应用. 2013,…
CUDA编程模型系列八(原子操作 / 规约 / 向量元素求和)
本系列视频目的是帮助开发者们一步步地学会利用CUDA编程模型加速GPU应用, 我们的口号是: 让GPU飞起来
本期我介绍了cuda 当中规约算法的一种情况, 也是小何尚职业生涯中的第一道面试题, 计算数组中所有元素的和. CUDA编程模型系列八(原子操作 / 规约 / 向量元素求和) #include…
数据结构--特殊矩阵的压缩存储
数据结构–特殊矩阵的压缩存储 一维数组的存储结构
ElemType a[10]; //ElemType型一维数组各数组元素大小相同,且物理上连续存放。 数组元素a[i]的存放地址 LOC i * sizeof(ElemType) ( 0 ≤ i < 10 ) (0\le i < 10) (0≤i<10) 注:除非题目特别说明&…
【Matlab任务分配】蚁群算法无人机任务分配【含源码 1265期】
一、代码运行视频(哔哩哔哩)
【Matlab任务分配】蚁群算法无人机任务分配【含源码 1265期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业…
矩阵和矩阵乘法的直观化理解
本文分享矩阵和矩阵乘法的直观化理解
矩阵是一种非常好用的数学工具, 刚开始是为了求解线性方程组而被发明出来. 随着线性代数在各个领域的广泛应用而得到巨大的发展.
因为矩阵是一种非常抽象的概念和工具, 矩阵乘法更是让不少人摸不着头脑, 作者在多年的学习和实践中有了一些…
【Matlab车间调度】粒子群算法求解6X6车间调度问题【含源码 411期】
一、代码运行视频(哔哩哔哩)
【Matlab车间调度】粒子群算法求解6X6车间调度问题【含源码 411期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电…
半正定松弛法(SDR)2021-11-06
[TOC](半正定松弛法 ( Semidefinite Relaxation) 求解二次优化问题(QCQP))
SDR适用问题的表现形式 minx∈RnxTCxs.t.xTAix⊵ibi,i1,⋯,m,\min_{x \in \mathbb{R} ^n} ~~ x^TCx \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm {s.t.} ~~x^TA_ix \unr…
数值分析(13):常微分方程的数值解法之线性多步法
线性多步法1. 引言2. 线性多步法基本概念2.1 迭代表达式2.2 局部截断误差,阶,主局部截断误差3. 一些常见的线性多步法3.1 显式Adams方法3.2 隐式Adams方法3.3 预估一校正方法1. 引言
除了Runge-Kutta方法是否还有提高精度的方法?
回答是肯定…
数值分析(11):常微分方程的数值解法之Euler法
常微分方程的数值解法之Euler法1. 引言2. Euler方法2.1 显式Euler方法2.2 隐式Euler方法2.3 梯形方法3. 隐式方程的迭代求解4. 预估-校正方法5. 误差分析5.1 显式单步方法误差分析5.2 隐式单步方法误差分析1. 引言
我们通常遇到的一阶常微分方程初值问题,如下所示&…
数值分析(10):数值积分之Gauss型求积公式
Gauss型求积公式1. 引言2. Gauss型求积公式2.1 Gauss型求积公式的定义2.2 Gauss点的性质2.3 构造Gauss型求积公式2.4 Gauss型求积公式的余项2.5 Gauss型求积公式的稳定性与收敛性2.6 Gauss-Legendre求积公式2.7 Gauss-Chebyshev求积公式1. 引言
在前一章《数值分析(9)…
数值分析(9):数值积分之Newton-Cotes求积公式和复合求积公式
数值积分之Newton-Cotes求积公式和复合求积公式1. Newton-Cotes求积公式1.1 N-C求积公式的推导1.2 N-C求积公式的余项1.3 N-C求积公式的数值稳定性2. 复合求积公式2.1 复合梯形求积公式2.2 复合Simpson求积公式1. Newton-Cotes求积公式
1.1 N-C求积公式的推导
在《数值分析(8…
计算方法 6.插值法
需求的由来: 插值法定义: 唯一性: 其实就是一个多元方程组嘛。 这个完全就是数字游戏吧,后面那一项永远是0. 拉格朗日求法: Ln(x)就是p(x)。里面有yi作为系数,求这样的li应该是什么样。 可以看到࿰…
CF718C Sasha and Array 题解
CF718C Sasha and ArrayCF718C Sasha and Array 重点: 矩阵乘法 a(bc)abaca\times(b c) ab aca(bc)abac。 而且矩阵乘法是有结合律的:abca(bc)a \times b \times c a\times (b\times c)abca(bc) 但是 没有\color{red}\text{没有}没有 交换律…
线性代数的本质(笔记三)
点积与对偶性(Dot products and duality)
点积的运算
点积(点乘,数量积,内积)的标准方法: 两个维数相同的向量,将相应的坐标配对,求出每一对的乘积,然后相…
线性代数Python计算导引
线性代数是深度学习的数学基础之一,理论完备,方法经典。Python是当下AI系统首选开发工具,易学好用。教学中攒下两者结合的多个课题,覆盖大学理工科《线性代数》课程内容,写成博文以飨读者。今按课程大纲内容编排顺序&a…
计算方法 3.线性方程组解法
线性方程组的基本解法: 或者是迭代法: 向量范数: 向量范数就是一些与向量有关的数。 矩阵范数: 常见的矩阵范数: 经典做法:高斯消元 类似的消元法: 列选消元: 全主元素消元法&#x…
机器学习数学基础之四多维高斯分布
多维高斯分布
概率密度函数
首先给出多维高斯分布的概率密度函数: p(x∣μ,Σ)1(2π)p2∣Σ∣12exp{−12(x−μ)TΣ−1(x−μ)}p(x|\mu,\Sigma)\frac{1}{(2\pi)^{\frac{p}{2}}|\Sigma|^{\frac{1}{2}}}exp\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\}p(x∣μ,Σ)(…
机器学习数学基础之三奇异值分解(SVD)
奇异值分解(Singular Value Decomposition,SVD)
引入
在上一节中我们回顾了矩阵的特征分解,但是特征分解只能对方阵进行(当然有的方阵可能也无法进行特征分解),那对于任意的一个矩阵 A∈RmnA\…
机器学习数学基础之二方阵的特征分解
机器学习数学基础之二方阵的特征分解
方阵的特征分解
特征分解的内容在《线性代数》这门课程里边讲过,现在算是对相关内容做一下简单回顾。
【特征值&特征向量】:对于方阵 AAA,若存在一个数 λ\lambdaλ 和一个向量 v⃗\vec{v}v使得 A…
鲁棒主成分分析RPCA
WHY?
传统的PCA算法对于噪音敏感,于是有人提出了RPCA将一个含有稀疏噪声的数据矩阵分解为低秩矩阵和稀疏噪音矩阵两部分。
WHAT? HOW? CODE
import numpy as np
import pandas as pd
Y数据矩阵alpha 步长pre 收敛的精度r 低秩为多少def RPCA(Y,alp…
MATLAB学习笔记5:绘图基础与数据可视化(中)
阅读前请注意:
1. 该学习笔记是华中师范大学HelloWorld程序设计协会2021年寒假MATLAB培训的学习记录,是基于培训课堂内容的总结归纳、拓展阅读。博客内容由 K2SO4钾 撰写、编辑,发布于 K2SO4钾 的个人投稿与华中师范大学HelloWorld程序设计协…
线性代数中两个向量相乘_加两个向量| Python的线性代数
线性代数中两个向量相乘Prerequisite: Linear Algebra | Defining a Vector 先决条件: 线性代数| 定义向量 In the python code, we will add two vectors. We can add two vectors only and only if the both the vectors are in the same dimensional space. For…
矩阵逆| 使用Python的线性代数
Prerequisites: 先决条件: Defining a Matrix 定义矩阵 Syntax: 句法: inv_M numpy.linalg.inv(M)Here, "M" is the matrix. 在此,“ M”是矩阵。 Python代码查找矩阵的逆 (Python code to find the inverse of a matrix) # Li…
QR法求解特征值特征向量
一 QR原理
理论依据:任意一个非奇异矩阵(满秩的方阵)A都可以分解为一个正交矩阵Q和一个上三角矩阵R的乘积,且当R对角元符号确定时,分解是唯一的。QR分解是一种迭代方法,迭代格式如下: 当Ak基本…
【Matlab雷达通信】中重频PD雷达仿真系统【含GUI源码 1055期】
一、代码运行视频(哔哩哔哩)
【Matlab雷达通信】中重频PD雷达仿真系统【含GUI源码 1055期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 沈再阳.精通MATLAB信号处理[M].清华大学出版社,2015. [2]高宝建,彭进业,王琳,潘…
matlab中各种括号(),[],与{}的区别与认识
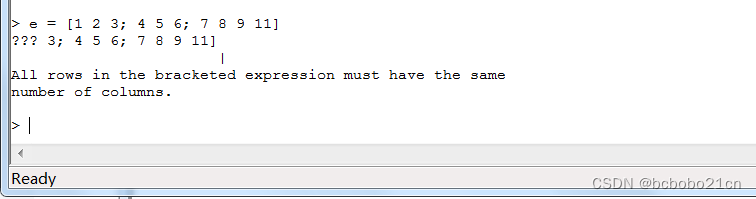
原文 在matlab中,常常会遇到(),[],和{},这个3种符号怎么区分,怎么用,这里我来总结一下,以供参考。 [] 首先。[]叫中括号,它用来存储矩阵和向量(vector在C中也叫容器) 举个例子&#…
带你深入理解矩阵乘法
为了不浪费大家宝贵的时间,开头我先简要说明一下这篇博文对哪些读者可能会有帮助
1、你是正在学习矩阵的乘法运算,觉得矩阵的乘法掌握起来很困难
2、你已经学会了矩阵乘法,但如果你在计算矩阵乘法时还在使用“一行乘一列得一数”的方法&…
线性代数矩阵转置乘法_转置矩阵的行列式| 使用Python的线性代数
线性代数矩阵转置乘法Prerequisite: 先决条件: Defining Matrix using Numpy 使用Numpy定义矩阵 Determinant of a Matrix 矩阵的行列式 Transpose Matrix 转置矩阵 Here, we will learn that the determinant of the transpose is equal to the matrix itself. Th…
文章翻译——矩阵微积分
文章作者:Sourya Dey 发表时间: 01 April 2019. 原文:https://www.researchgate.net/publication/332131671_Matrix_Calculus
目录: 文章目录1. 符号2. 基本规则3. 导数类型3.1 标量对标量(求导)3.2 标量对…
operands could not be broadcast together with shapes解决方案
矩阵相乘遇到:operands could not be broadcast together with shapes (163,5652) (5652,1) 先描述一下:
train_x.T 是一个(163,5662) 的ndarrayLost 是一个(5662, 1)的ndarray
这里我大概明白哪里错了&a…
[文章推荐]Matrices from a geometric perspective
发现一篇不错的文章,从geometry角度重新介绍了点、向量、坐标、坐标系、矩阵等等概念,读完还是有收获的。链接如下:Matrices from a geometric perspective | Coranachttps://www.coranac.com/documents/geomatrix/
SDR算法的应用 2021-12-20
SDR算法的使用回顾EVD 分解高斯随机化参考链接回顾
接上面的工作 SDR,SDR处理的QCQP问题形式为: minx∈RnxTCxs.t.xTAix⊵ibi,i1,⋯,m,\min_{x \in \mathbb{R} ^n} ~~ x^TCx \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm {s.t.} ~~x^TA_ix \unrhd…
75、美团算法题---对角线遍历数组
一、题目1:对角线遍历I
(1)题目
给你一个大小为 m x n 的矩阵 mat ,请以对角线遍历的顺序,用一个数组返回这个矩阵中的所有元素。 (2)思路
根据题目描述,首先仔细找一下这道题中一…
66、十进制转换为M进制
一、十进制转换为二进制、八进制、十六进制
将十进制转换为其它进制时比较复杂,整数部分和小数部分的算法不一样,下面我们分别讲解。
1) 整数部分
十进制整数转换为N进制整数采用“除N取余,逆序排列”法。具体做法是:
将N作为…
leetcode-----给出一个用二维矩阵表示的图像 返回该图像顺时针旋转90度的结果
题目描述
给出一个用二维矩阵表示的图像
返回该图像顺时针旋转90度的结果
扩展:
你能使用原地算法解决这个问题么? public void rotate(int[][] matrix) {//分两步进行处理(总共旋转了90)/*1)沿yx对角线进行翻转(即…
广州套刷公交卡数学建模
广州套刷公交卡数学建模前言一、问题描述二、数学建模三、问题求解总结前言
广州乘坐公交地铁优惠方案如下:每月前15次9.5折,第16次开始6折。公交通常是2元一次,地铁按里程分段收费,起步价格为2元。有的乘客单次乘坐地铁原价比较…
龙格-库塔(Runge-Kutta)
龙格-库塔是求解非线性常微分方程的一种方法,本文介绍了利用 python 实现龙格-库塔的方法。
1. 龙格-库塔公式 方程的导数和初值: 方程的迭代计算公式: 其中, 2. 实例 有一个方程,其微分方程和初值:&…
C#,数值计算——灰色码(Gray Codes)的计算方法与源代码
一个 n位灰色码 序列,就是2的n次方 个 整数;
第一个数字为0;
相邻两个数字的二进制只有一位不一样;
第一个数字和最后一个数字的二进制也只有一位不一样。 using System;
namespace Legalsoft.Truffer { /// <summary&…
3.5 螺旋矩阵 II
59 螺旋矩阵 II题目给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。思路具体代码实现(C)模型(知识点)题目
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素…
CG(conjugate gradient method)+Python+Matlab
没时间敲公式、截个图Matlab程序:
python
% ** 文件名:Conjugate Gradient.m
%
% ** 日 期:2016.12.14
%
% ** 描 述:共轭梯度法解线性方程组(Conjugate Gradient method)
%
% ** 函数:113页计算实习3.2
%
% ** 参考教材&a…
Python scipy linalg.solve_toeplitz
用法: scipy.linalg.solve_toeplitz(c_or_cr, b, check_finiteTrue) 使用Levinson递归求解Toeplitz系统
Toeplitz矩阵具有恒定的对角线,其中c为第一列,r为第一行。如果没有给出rr conjugate©假设。
参数: c_or_cr…
Matlab CH4 线性规划
文章目录代码练习问题代码练习 例1 %%% 线性规划 例1
clc;
c [6 3 4 ];
A [1 2 -3; 0 1 0];
B [80; 50];
Aeq [1 1 1];
Beq [120];
vlb [30 0 20];
vub [];
[x, fval] linprog(c, A, B, Aeq, Beq, vlb, vub);
% c 是不等式系数
% A B 是不等式约束条件 A是系数&#x…
常用 - 现代希腊字母对应代码
序号字母大写字母小写对应代码汉语读法1A\AlphaAα\alphaα\alpha阿尔法2B\BetaBβ\betaβ\beta贝塔3Γ\GammaΓγ\gammaγ\gamma伽玛4Δ\DeltaΔδ\deltaδ\delta德尔塔5Eε\varepsilonε\varepsilon埃普西隆6Z\ZetaZζ\zetaζ\zeta泽塔7H\EtaHη\etaη\eta伊塔8Θ\ThetaΘθ\…
MATLAB - 拉普拉斯算子可视化
1、拉普拉斯算子∇2\nabla^ 2∇2
拉普拉斯算子有很多用途,在物理中常用于波动方程、热传导方程和亥姆霍兹方程的数学模型;在静电学中,拉普拉斯方程和泊松方程的应用随处可见;在数学中,经拉普拉斯算子运算运算为零的函…
MATLAB - 散度可视化
1、通量与散度
1)通量ψ∫dψ∫SF⃗⋅dS⃗∫SF⃗⋅e⃗ndS\psi\int \mathrm{d} \psi\int_{S} \vec{F} \cdot \mathrm{d} \vec{S}\int_{S} \vec{F} \cdot \vec{e}_{\mathrm{n}} \mathrm{d} Sψ∫dψ∫SF⋅dS∫SF⋅endS其中: dS⃗e⃗ndS\mathrm{d} \…
MATLAB - 梯度可视化
1、梯度(gradugradugradu或∇u\nabla u∇u)
1)概念: ∇ue⃗l∂u∂l∣max\nabla u\left.\vec{e}_{l} \frac{\partial u}{\partial l}\right|_{\max }∇uel∂l∂u∣∣∣∣max 2)意义:描述标量场在…
MATLAB - 矢量函数可视化
1、meshgrid函数
在利用MATLAB进行3D图形绘制时,往往需要一些采样点,然后根据采样点进行图形绘制。meshgrid函数是用于生成网格采样点的函数,示例如下:
x-3:1:3;
y-2:1:2;
[X,Y]meshgrid(x,y)运行结果: 运行结果如…
Java机器学习-BLAS线性代数
一.认识 BLAS【Basic Linear Algebra Subprograms,基础线性代数程序集】是一个抽象类,用于规范发布基础基础线性代数操作的数值库【常用于向量或矩阵计算】。该程序集最初发布于1979年,并用于创建更大的数值程序包【例如:LAPACK】…
归一化和相关性的计算
1.认识归一化 总结1:归一化是使计量(物理)系数值的绝对值变成某种相对值的相关性办法 总结2:在以前的本科化学的量子学里,表达粒子的量子态的波函数必须满足归一条件,也就是说,在空间内找到粒子…
向量叉乘后再左乘矩阵
若RRR是正定矩阵,即RTR−1R^{T}R^{-1}RTR−1, ∣R∣1|R|1∣R∣1,则下面公式成立: R(ab)(Ra)(Rb)R(a \times b) (Ra) \times (Rb) R(ab)(Ra)(Rb) 看一下仿真验证:
phi pi/9;
theta pi/10;
psi pi/8;
R_phi_T [1, 0, 0;.…
视觉SLAM14讲笔记05:ch7三角测量,PnP,ICP
三角测量 考虑图像 I1I_{1}I1 和 I2,I_{2},I2, 以左图为参考,右图的变换矩阵为 TTT 。相机光心为 O1O_{1}O1 和 $O_{2} 。在。 在。在I_{1}$ 中有特征点 p1,p_{1},p1, 对应 I2I_{2}I2 中有特征点 p2p_{2}p2 。理论上直线 O1p1O_{1} p_{1}O1p1 与 O2…
视觉SLAM14讲笔记04:ch7对极几何(epipolar geometry)
2D-2D:对极几何(epipolar geometry)
对极约束
现在,假设我们从两张图像中,得到了一对配对好的特征点,像图7-7里显示的那样。如果我们有若干对这样的匹配点,就可以通过这些二维图像点的对应关系,恢复出在两帧之间摄像…
使用Quaternion.AngleAxis和Quaternion.Euler实现目标点绕某点旋转
target 是目标点Vector3
org 是自身点Vector3
-45f是旋转的角度
Vector3.up是绕y轴
Vector3 pos Quaternion.AngleAxis(-45f, Vector3.up) * (target - org) org;
也可以是
Vector3 pos Quaternion.Euler(0f, -45f, 0f) * (target - org) org;
Quaternion.Euler 和 …
线性代数感悟之4 通过增广矩阵查看解的情况上篇
最近在看 liuyubobobo 的 线性代数 课,感觉很妙,有些感悟记录一下~~~
通过增广矩阵查看解的情况: ------------------------------------------------------------------------------------------------------------------------------
主…
(邱维声)高等代数课程笔记:目录
(邱维声)高等代数课程笔记:目录
高等代数课程 - 邱维声
引言 高等代数的研究对象 高等代数的主线 线性空间的结构及其线性映射一元多项式环的结构及其通用性质 第1章 线性方程组的解法 1.1 解线性方程组的矩阵消元法1.2 线性方程组解的情况…
新的开始(最小生成树)
题目描述 发展采矿业当然首先得有矿井,小 FF 花了上次探险获得的千分之一的财富请人在岛上挖了 n 口矿井,但他似乎忘记考虑的矿井供电问题……
为了保证电力的供应,小 FF 想到了两种办法:
在这一口矿井上建立一个发电站…
顺序表(vector)------实现(模板类)
向量(Vector):
是一个封装了动态大小数组的顺序容器(Sequence Container)。跟任意其它类型容器一样,它能够存放各种类型的对象。可以简单的认为,向量是一个能够存放任意类型的动态数组。 下方链…
线性代数Python计算:向量组的最大无关组计算
对给定的mmm-维向量组 α1(a11a21⋮am1),α2(a12a22⋮am2),⋯,αn(a1na2n⋮amn)\boldsymbol{\alpha}_1\begin{pmatrix}a_{11}\\a_{21}\\\vdots\\a_{m1}\end{pmatrix},\boldsymbol{\alpha}_2\begin{pmatrix}a_{12}\\a_{22}\\\vdots\\a_{m2}\end{pmatrix},\cdots,\boldsymbol{\al…
线性代数Python计算:Python的位运算
Python中整数在机器内部是按按二进制格存储的,每一位非0即1。因此,每一位都构成了布尔代数(B,∨,∧,)(B,\vee,\wedge,\neg)(B,∨,∧,)以及域(B,⊕,∧)(B,\oplus,\wedge)(B,⊕,∧),其中B{0,1}B\{0,1\}B{0,1},∨,∧,,⊕\vee,\wedge,…
线性代数学习笔记(四)——行列式按行展开
本篇笔记介绍了行列式按行或按列展开定理、异乘变零定理、拉普拉斯定理和行列式相乘定理。
1 行列式按行(列)展开定理
余子式:去掉行列式指定元素所在行和所在列元素后得到的新行列式(顾名思义,即剩余子集行列式&…
线性代数学习笔记(三)——行列式的性质
本篇文章首先引入行列式转置的概念,然后逐一给出了行列式的七个基本性质,需要注意的是:对行成立的性质对列也同样成立。最后强调了性质7的重要性,并总结了在做题过程中的规范和注意事项。
1 转置
将行列式的行做成列,…
微积分中计算椭圆面积的几种方法
Find the area enclosed by the ellipse x2a2y2b21\frac{x^2}{a^2}\frac{y^2}{b^2}1a2x2b2y21 Trigonometric Substitutions yb1−x2a2yb \sqrt[]{1-\frac{x^2}{a^2}}yb1−a2x2 let xasinθxa\sin\thetaxasinθ then ybcosθyb\cos\thetaybcosθ , dxacosθdθdx…
markdown 数学公式Latex语法
在输入数学公式的时候,需要在数学公式的前后加入$符号,将需要输入的公式加入到$中间。
行内公式
$行内公式$行间公式
?
行间公式
?角标(上下标)
上标 ^下标 _
名称数学表达式markdown公式上标aba^bab$a^b$下标aba_bab$a_…
朴素贝叶斯,支持向量积,Fisher分类器的简单数学原理推导
1.朴素贝叶斯算法(Naive Bayes) 2.支持向量机(Support Vector Machine,SVM)的wolf对偶模型 3.Fisher分类器or线性判别分析(Linear Discriminant Analysis,LDA)
抖音矩阵系统源码开源部署分享(三)
目录 一、 概述:
二、 账号矩阵搭建目的: 三、 抖音矩阵系统源码开发步骤
四、 功能规划 五、 代码开发展示 一、 概述:
抖音矩阵系统是指通过多个账号运营,对账号之间的内容和特征进行细分,账号之间相互引流推广&a…
基于Gurobi的列生成算法
前言
列生成算法是求解大规模线性规划的有效手段之一,对于难以直接求解的大规模线性规划问题,列生成在某些场景能够缩小问题规模,降低问题求解难度,在可接受的时间内精确求解问题。列生成的基本思路是将一个原问题从一个小的模型…
来了!安利一款助力百度世界2020 “5G云代驾”、直播互动的黑科技
携手央视新闻,百度世界2020重磅来袭。尽管活动采取直播形式,与观众隔着屏幕的距离,但各种黑科技带来的冲击感依旧非常强烈。今天,先来揭秘此次大会“5G云代驾”、互动直播的背后黑科技之一—百度智能云实时音视频RTC。什么是RTC&a…
欧拉角,四元素,旋转矩阵
#1.欧拉角(roll, pitch, yaw) 滚转角Φ(roll):围绕X轴旋转的角度 俯仰角θ(pitch):围绕Y轴旋转的角度 偏航角ψ(yaw):围绕Z轴旋转的角度 描述物体在参考坐标系下的姿态&a…
Python 实现实现Numpy找到最大值的位置(PCA的实现)
np.sort()函数的作用,从小到大排序。(这里我也需要注意axis) 不写的话他的默认值为1. 使用x np.max(x) 获得一个掩模矩阵,然后使用where方法即可返回最大值对应位置。 编程PCA算法的时候
xnp.array([[-1,-1,0,2,0],[-2,0,0,1,1…
基于Cplex的分支定界
前言
分支定界算法是求解整数规划的最常用方法之一,它不仅适用于纯整数规划问题,也适用于混合整数规划问题。分支定界的基本思想是将可行区域分解为越来越小的区域,这一过程为分支过程,对于结果劣于当前界的分支,可以…
宋浩线性代数笔记(五)矩阵的对角化
本章的知识点难度和重要程度都是线代中当之无愧的T0级,对于各种杂碎的知识点,多做题复盘才能良好的掌握,良好掌握的关键点在于:所谓的性质A与性质B,是谁推导得谁~
第四章,向量组,3-线性相关性
第四章,向量组,3-线性相关性 线性相关性的定义线性相关性的判断根据定义来判断(例见原文)线性表示法判断秩法判断行列式判断 方程法 结论结论1结论2结论3 玩转线性代数(24)线性相关性的笔记,相关证明以及例子见原文 线…
2023-8-14 子矩阵的和
题目链接:子矩阵的和
#include <iostream>using namespace std;int n, m, q;
const int N 1010;int a[N][N], s[N][N];int main ()
{scanf("%d%d%d", &n, &m, &q);for(int i 1; i < n; i )for(int j 1; j < m; j)scanf(&quo…
抖音seo矩阵系统源代码开发部署分享
一、 开发步骤分享
抖音SEO矩阵系统源代码开发部署分享,需要经验丰富的开发人员和服务器管理人员,以下是大致的步骤: 确定你需要的功能和设计,确定开发人员和设计师的角色和任务分配,以及开发进度和计划。 确定服务器…
代码随想录训练营二刷第二天 | 977.有序数组平方 209.长度最小的子数组 904. 水果成篮 59.螺旋矩阵II
代码随想录训练营二刷第二天 |
一、977.有序数组平方
题目链接 思路:数组是有序的,平方后最大值只会出现在数组两端,因此可以使用双指针法从两端选取最大值放在新数组的尾部。
class Solution {public int[] sortedSquares(int[] nums) {i…
LA@向量运算@内积@向量正交
文章目录 内积符号说明向量内积性质对称性线性性正定性 推论:柯西-布尼亚科夫斯基-施瓦茨公式(柯西不等式)解系几何向量的数量积和线性代数向量内积n维向量的长度(范数)向量长度的性质单位向量单位化 向量夹角 向量正交标准正交正交向量组正交向量组线性无关记号补充Note例 标准…
【考研数学】线性代数第四章 —— 线性方程组(2,线性方程组的通解 | 理论延伸)
文章目录 引言四、线性方程组的通解4.1 齐次线性方程组4.2 非齐次线性方程组 五、方程组解的理论延伸 引言
承接前文,继续学习线性方程组的内容,从方程组的通解开始。 四、线性方程组的通解
4.1 齐次线性方程组
(1)基础解系 —…
线性代数的学习和整理14: 线性方程组求解
目录
1 线性方程组
2 有解,无解
3 解的个数 1 线性方程组 A*xy 3根直线的交点,就是解 无解的情况
无解: 三线平行无解:三线不相交
有解
有唯一解:三线相交于一点有无数解:三条线重叠 2 齐次线性方程组…
【学习笔记】求解线性方程组的G-S迭代法
求解线性方程组的G-S迭代法
// 运行不成功啊function [x,k,index] Gau_Seid(A,b,ep,it_max)
% 求解线性方程组的G-S迭代法,其中
% A为方程组的系数矩阵
% b为方程组的右端项
% ep为精度要求,省缺为1e-5
% it_max为最大迭代次数,省缺为100
% …
个人笔记——格林巴赫范式转化为NPDA
哥伦巴赫范式转换为NPDA规则:
1.首先增加开始转移和结束转移: &(q0 ,ε , z)(q1 , Sz) & (q1 , ε , z)(qf , z)
2.根据规则得到转移函数 形如A→aω,其中ω中的元素均是非终结符, 则增加状态:&a…
【考研数学】线形代数第三章——向量 | 3)向量组秩的性质、向量空间、过渡矩阵
文章目录 引言三、向量组等价、向量组的极大线性无关组与秩3.2 向量组秩的性质 四、 n n n 维向量空间4.1 基本概念4.2 基本性质 写在最后 引言
紧接前文学习完向量组秩的基本概念后,继续往后学习向量的内容。 三、向量组等价、向量组的极大线性无关组与秩
3.2 向…
SLAM中的三角化方案
Linear triangulation methods 又称为线性三角形法,其作用是通过同一个三维空间点在两个视图中的平面坐标(也可以认为是像素坐标),求解这个三维空间点的世界坐标。通常的求解方式有两种,一种是数值求解;一种…
线性代数-初等行变换与初等行矩阵
定义
初等行变换:在矩阵的行上进行倍加、倍乘、对换变换 初等行矩阵:在单位矩阵上应用初等行变换得到的矩阵
初等行矩阵乘上矩阵,就相当于在矩阵上实施了对应的初等行变换。
**
以矩阵为例:
** 倍加:将第二行乘2加…
python实现SOR迭代法
照着上面的式子写
def SOR(A,b,x,e,w,times100):#A为方程组系数矩阵#b为右端向量#x为初始解#e为误差大小#w为松弛因子#times为迭代次数D np.mat(np.diag(np.diag(A)))L np.triu(A, 1)U np.tril(A, -1)Sw (Dw*L).I*((1-w)*D-w*U)fw w*((Dw*L).I)*bx0xx Sw * x0 fwk 1w…
视觉SLAM14讲笔记-第3讲-三维空间刚体运动
空间向量之间的运算包括: 数乘、加法、减法、内积、外积。 内积:可以描述向量间的投影关系,结果是一个标量。 a ⃗ ⋅ b ⃗ ∑ i 1 3 a i b i ∤ a ∤ ∤ b ∤ c o s ⟨ a , b ⟩ \vec{a} \cdot \vec{b}\sum_{i1}^3{{a _i}{b_i}} \nmid a…
【理解线性代数】(二)线性运算和线性空间
1. 从112看线性运算
11为什么等于2?其实11等于2有一个前提条件,那就是必须在线性运算规则下进行。什么是线性运算规则呢?
理解起来很简单,在一条直线上, 一米的直线长度一米的直线长度两米的直线长度 两个数相加的结…
知识储备--基础算法篇-矩阵
2.矩阵
2.1第54题螺旋矩阵
第一题上来就跪了,看了官方答案感觉不是很好理解,找了一个比较容易理解的。
class Solution(object):def spiralOrder(self, matrix):""":type matrix: List[List[int]]:rtype: List[int]"""…
SLAM从入门到精通(矩阵的使用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 学习SLAM,离开了矩阵肯定是玩不转的。大学数学里面除了微积分,剩下的就是线性代数和概率论。而矩阵就是线性代数的一部分。…
P2801 教主的魔法 —— 分块+sort+暴力
P2801 教主的魔法 写分块的时候一定要注意什么时候用l, r 什么时候用bel[x],bel[y],一不注意就容易出错 // Decline is inevitable,
// Romance will last forever.
#include <bits/stdc.h>
using namespace std;
#define mst(a, x) memset(a, x…
matlab求解线性规划问题
matlab求解一般线性规划问题1. 普通线性规划问题符号说明(1)列出约束条件与目标函数(2) 调用matlab函数(1)函数介绍:(2)调用函数:(3)输出结果:(4)代码解释:(3)练习&#…
【稀疏数组】二维数组与稀疏数组之间的转换及文件存储
稀疏数组是干什么用的?在什么情况下该使用稀疏数组呢?
当一个数组中的大部分元素为0,或者为同一个值的数组时,可以使用稀疏数组来保存该数组。
稀疏数组是一个sum1行3列的矩阵sum为不同元素的个数。 稀疏数组的第一行保存的是原…
Linear Decryption: Rate-1 FHE TLP
参考文献: [ILL89] Russell Impagliazzo, Leonid A. Levin, and Michael Luby. Pseudo-random generation from oneway functions (extended abstracts). In 21st Annual ACM Symposium on Theory of Computing, pages 12–24, Seattle, WA, USA, May 15–17, 1989.…
求解矩阵最小路径和(详细分析)
求解矩阵最小路径和给定一个m行n列的矩阵,从左上角开始每次只能向右或者向下移动,最后到达右下角的位置,路径上的所有数字累加起来作为这条路径的路径和。如下面一个4行4列的矩阵:
1 3 5 9
8 1 3 4
5 0 6 1
8 8 4 0
1→3→1→0→6…
矩阵系统全方位管理多平台1000多个账号,实现精准化运营获客!
全自动化视频综合处理工具!
普通的剪辑软件是不可能实现自动化,一个人一天制作3000条视频!必须要借助高效率的工具【呆头鹅批量剪辑软件】探店混剪系统,导入大量的素材,就能自动帮你批量处理,满…
03 MIT线性代数-矩阵乘法和逆矩阵Multiplication inverse matrices
1. 矩阵乘法 Matrix multiplication
我们通过四种方法讨论如何使矩阵A与B相乘得到矩阵C。其中A为mxn(m行n列)矩阵,而B为nxp矩阵,则C为mxp矩阵,记cij为矩阵C中第i行第j列的元素
1.1 Regular way
矩阵乘法的标准计算方…
LeetCode——剑指 Offer 29【顺时针打印矩阵】
题目
剑指 Offer 29. 顺时针打印矩阵
题目概述
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
限制:
0 < matrix.length < 1000 < matrix[i].length < 100
示例 输入:matrix [[1,2,3],[4,5,6],[7,8,9]]
…
分式理想 对偶群 对偶空间
参考文献:
Deitmar A. A first course in harmonic analysis[M]. 2005.Ideal quotient | encyclopedia article by TheFreeDictionaryFractional ideal | encyclopedia article by TheFreeDictionaryPontryagin duality | encyclopedia article by TheFreeDictiona…
【每日一题】74. 搜索二维矩阵
74. 搜索二维矩阵 - 力扣(LeetCode) 给你一个满足下述两条属性的 m x n 整数矩阵: 每行中的整数从左到右按非递减顺序排列。每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返…
【线性代数及其应用 —— 第一章 线性代数中的线性方程组】-1.线性方程组
所有笔记请看:
博客学习目录_Howe_xixi的博客-CSDN博客https://blog.csdn.net/weixin_44362628/article/details/126020573?spm1001.2014.3001.5502思维导图如下: 内容笔记如下:
【问题证明】矩阵方程化为特征值方程求得的特征值为什么是全部特征值?不会丢解吗?
问题
这个问题困扰了我好久,一直感觉如果有其他的特征值没法证伪,不过一直存在思想的层面,没有实际解决,今天突然想到动笔来解决,遂得解,证明如下。
证明 总结
这个证明看似证明过后很直观,但…
贪心+二分+DP+矩阵快速幂:CF461E
https://codeforces.com/contest/461/problem/E
第一步:捕捉题目信息
四种字符 → \to → 矩阵 n ≤ 1 0 18 → n\le 10^{18}\to n≤1018→ 矩阵快速幂 → \to → dp最小值最大 → \to → 二分
第二步:分析性质 s s s 未知?那如果已知怎…
线性代数的本质(九)——二次型与合同
文章目录 二次型与合同二次型与标准型二次型的分类度量矩阵与合同 二次型与合同
二次型与标准型 Grant:二次型研究的是二次曲面在不同基下的坐标变换 由解析几何的知识,我们了解到二次函数的一次项和常数项只是对函数图像进行平移,并不会改变…
day2| 977.有序数组的平方、209.长度最小的子数组、 59.螺旋矩阵II
977.有序数组的平方 题目链接:https://leetcode.cn/problems/squares-of-a-sorted-array/ 文章讲解:https://programmercarl.com/0977.%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E7%9A%84%E5%B9%B3%E6%96%B9.html 视频讲解: https://www.bilibil…
【考研数学】线性代数第六章 —— 二次型(1,基本概念)
文章目录 引言一、二次型的基本概念及其标准型1.1 基本概念 写在最后 引言
所谓二次型即所有项都是二次的多项式,当一个二次型只有平方项而没有交叉项时,该二次型称为标准二次型。
这是线代的最后一个章节了,也确实很久没看线代了ÿ…
学习记忆——数学篇——案例——代数——方程——一元二次方程
重点记忆法 a x 2 b x c 0 ax^2bxc0 ax2bxc0 整体可以由: 根 ⟹ \Longrightarrow ⟹ △ △ △ ⟹ \Longrightarrow ⟹ 求根公式 x 1 , 2 x_{1,2} x1,2 − b △ 2 a \frac{-b\sqrt{△}}{2a} 2a−b△ ⟹ \Longrightarrow ⟹ 韦达定理 ⟹ \Longrightarr…
线性代数-Python-01:向量的基本运算 -手写Vector -学习numpy的基本用法
文章目录 代码目录结构Vector.py_globals.pymain_vector.pymain_numpy_vector.py 一、创建属于自己的向量1.1 在控制台测试__repr__和__str__方法1.2 创建实例测试代码 二、向量的基本运算2.1 加法2.2 数量乘法2.3 向量运算的基本性质2.4 零向量2.5 向量的长度2.6 单位向量2.7 …
线性代数中涉及到的matlab命令-第三章:矩阵的初等变换及线性方程组
目录
1,矩阵的初等变换
1.1,初等变换
1.2,增广矩阵
1.3,定义和性质
1.4,行阶梯型矩阵、行最简型矩阵
1.5,标准形矩阵
1.6,矩阵初等变换的性质
2,矩阵的秩
3ÿ…
【问题思考总结】已知对角矩阵怎么求原矩阵?原矩阵唯一吗?【相似对角化】
问题
这个问题起源于2010年数一真题: 给定一个对角阵,说QTAQ对角阵,然后Q矩阵实际上是能求出来无穷个的,在这种情况下,A矩阵该怎么求?或者说,Q矩阵不同的时候,A矩阵唯一吗…
【数据结构】数组和字符串(二):特殊矩阵的压缩存储:对角矩阵——一维数组
文章目录 4.2.1 矩阵的数组表示4.2.2 特殊矩阵的压缩存储a. 对角矩阵的压缩存储结构体初始化元素设置元素获取打印矩阵主函数输出结果代码整合 4.2.1 矩阵的数组表示
【数据结构】数组和字符串(一):矩阵的数组表示
4.2.2 特殊矩阵的压缩存储…
796. 子矩阵的和(二维前缀和)
题目:
796. 子矩阵的和 - AcWing题库 思路:
1.暴力搜索(搜索时间复杂度为O(n2),很多时候会超时)
2. 前缀和(左上角(二维)前缀和):本题特殊在不是直接求前…
基于标签的电影推荐算法研究_张萌
2 标签推荐算法计算过程
2.1 计算用户对标签的喜好程度
用户对一个标签的认可度可以使用二元关系来表示,这种关系只有“是”“否”两种结果,实际上难以准确地表达出用 户对物品的喜好程度。因此&#x…
【机器学习(二) 线性代数基础I(Linear Algebra Foundations)】
机器学习(二) 线性代数基础I(Linear Algebra Foundations)
这一节主要介绍一些线性代数的基础。 目录 机器学习(二) 线性代数基础I(Linear Algebra Foundations)1. 向量 Vectors2. 复杂度 Complexity3.线…
线性代数 第三章 向量
一、运算
加法、数乘、内积
施密特正交化
二、线性表出
概念:如果,则称可由线性表出(k不要求不全为0)
判定:
非齐次线性方程组有解无关,相关
如果两个向量组可以互相线性表出,则称这两个…
线性代数 | 矩阵运算 加减 数乘 矩阵的幂运算
文章目录 1. 矩阵加减和数乘2.矩阵与矩阵的乘法2.1相乘条件:看中间,取两头2.2 相乘计算方法 3. 矩阵的幂3.1 观察归纳法3.2 邻项相消法3.3 化为对角 4.矩阵求逆(除法)4.1 判断是否可逆(证明题或者要求求出逆矩阵&#…
勘察设计考试公共基础之数学篇
1、数学
向量点积:向量叉积:平面的法向量为n(A,B,C),则该平面的点法式方程为:
A(x-x0)B(y-y0)C(z-z0)0
两平…
VINS-Mono-后端优化 (四:边缘化原理)
滑窗中固定只能有11帧,当来了新的帧的时候旧的帧就需要抹掉,但是不能直接把旧的帧的全部信息抹掉,因为旧的帧的经历过11次优化,其地图点中的优化信息是有用,边缘化的操作就是为了只把最旧帧的变量去掉,但是…
[量子计算与量子信息] 2.1 线性代数
2.1 线性代数
符号对照表 量子力学中,向量使用 ∣ ψ ⟩ \ket \psi ∣ψ⟩ (ket)来表示,可以理解为一个列向量。其对偶向量为 ⟨ ψ ∣ \bra \psi ⟨ψ∣ ,可以理解为行向量。
向量空间中零向量直接用 0 0 0 表示, ∣ 0 ⟩ \…
Unity中Shader矩阵的转置矩阵
文章目录 前言一、转置的表示二、转置矩阵三、转置矩阵的总结1、(A^T^)^T^ A2、(A B)^T^ A^T^ B^T^3、(kA)^T^ kA^T^ (k为实数)4、(AB)^T^ B^T^A^T^5、如果 A A^T^ 则称A为对称矩阵6、如果 AA^T^ I(单位矩阵),则称 A 为正交矩阵,同时 A^T^ A^-1…
2.4 矩阵的运算法则
矩阵是数字或 “元素” 的矩形阵列。当矩阵 A A A 有 m m m 行 n n n 列,则是一个 m n m\times n mn 的矩阵。如果矩阵的形状相同,则它们可以相加。矩阵也可以乘上任意常数 c c c。以下是 A B AB AB 和 2 A 2A 2A 的例子,它们都是 …
fast lio 2 保存每一帧的点云PCD和里程计矩阵 Odom 在txt文件
修改了源代码的 laserMapping.cpp 文件,替换为下面的代码就可以保存了,注意里面有一个路径,需要修改为你的电脑的路径 // This is an advanced implementation of the algorithm described in the
// following paper:
// J. Zhang and S. Singh. LOAM: Lidar Odometry an…
【数据结构与算法系列5】螺旋矩阵II (C++ Python)
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1: 输入:n 3
输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2:
输入:n 1
输出&am…
FO-like Transformation
参考文献:
[RS91] Rackoff C, Simon D R. Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack[C]//Annual international cryptology conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 1991: 433-444.[BR93] Bellare M…
线性代数的学习和整理22:矩阵的点乘(草稿)
4 矩阵乘法 A,B两个同阶同秩N阵,看上去结构一样,但两厢相乘,在做在右,地位差别巨大。
在左,你就是基,是空间的根本,是坐标系,是往哪去、能到哪的定海神针,是如来佛手&a…
基于PHP的短视频SEO矩阵系统源码开发
随着短视频市场的爆发式增长,越来越多的企业开始寻求在短视频领域建立自己的品牌形象,增加用户粘性和获取更多流量。为此,一套高效的短视频SEO矩阵系统源码显得尤为重要。本文将介绍基于PHP语言的短视频SEO矩阵系统源码开发,帮助读…
线性代数的本质(十)——矩阵分解
文章目录 矩阵分解LU分解QR分解特征值分解奇异值分解奇异值分解矩阵的基本子空间奇异值分解的性质矩阵的外积展开式 矩阵分解
矩阵的因式分解是把矩阵表示为多个矩阵的乘积,这种结构更便于理解和计算。
LU分解
设 A A A 是 m n m\times n mn 矩阵,…
前缀和——1314. 矩阵区域和
文章目录 🎤1. 题目🎤2. 算法原理🎤3. 代码实现 🎤1. 题目 题目链接:1314. 矩阵区域和 - 力扣(LeetCode) 给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer &#…
【视觉SLAM十四讲学习笔记】第四讲——李代数求导与扰动模型
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵 【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角 【视觉SLAM十四讲学习笔记】第三讲——四元…
MIT_线性代数笔记:第 08 讲 求解 Ax=b:可解性与结构
目录 可解的条件 Solvability conditions on b特解 A particular solution通解 Complete solution与零空间进行线性组合 Combined with nullspace 秩 Rank 可解的条件 Solvability conditions on b 矩阵 A 的第三行为第一行和第二行的加和,因此 Axb 中 b 的第 3 个分…
【参数估计】---点估计之矩估计
点估计之矩估计 👻什么是参数估计👻引例---理解参数估计🐟点估计🍭引例🍭点估计问题 🐟矩估计🍭预备知识🍭矩估计的求解步骤🍭矩估计例题 👻什么是参数估计 在…
关于Steering Vector的学习
关于Steering Vector的学习代码分析参考链接代码
首先,我们从matlab给出的Steering Vector文档开始入门,入门链接: https://ww2.mathworks.cn/help/phased/ref/steervec.html?s_tidsrchtitle
elementPos (0:.1:.4);
c physconst(LightSp…
保研CS/软件工程/通信问题汇总
机器学习
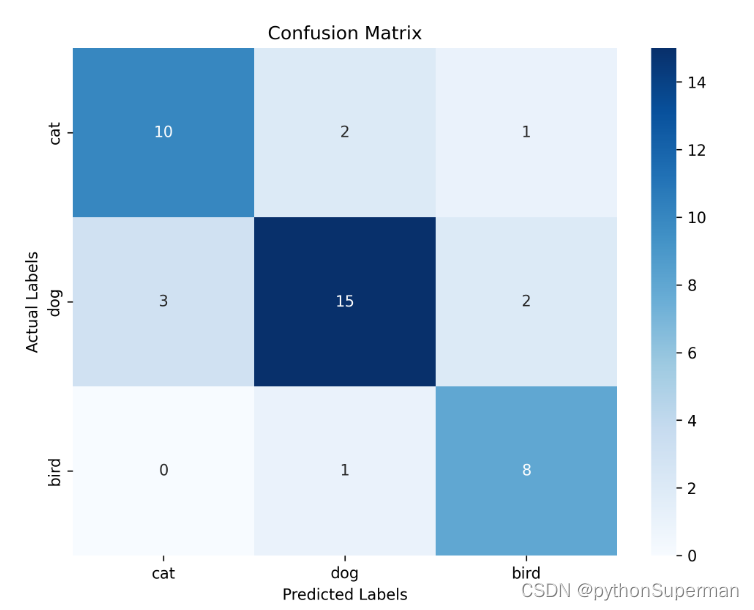
1.TP、TN、FP、FN、F1 2.机器学习和深度学习的区别和联系
模型复杂性:深度学习是机器学习的一个子领域,其主要区别在于使用深层的神经网络模型。深度学习模型通常包含多个隐层,可以学习更加复杂的特征表示,因此在某些任…
线性代数的学习和整理8: 方阵和行列式相关(草稿-----未完成)
1.4.1 方阵
矩阵里,行数列数的矩阵叫做方阵方阵有很多很好的特殊属性 1.4.2 行列式
行列式是方阵的一种特殊运算如果矩阵行数列数相等,那么这个矩阵是方阵。行列数的计算方式和矩阵的不同只有方阵才有行列式行列式其实是,矩阵变化的一个面…
半定规划(SDP) 2021-11-08
半定规划(SDP)凸优化简单回顾线性规划 (LP)二次规划 (QP)二阶锥规划 ( SOCP)半定规划(SDP)参考链接常见的凸优化问题包括:线性规划(LP,Linear Pro…
leetcode54. 螺旋矩阵(java)
螺旋矩阵 题目描述解题 收缩法 上期经典算法 题目描述 难度 - 中等 原题链接 - leecode 54 螺旋矩阵 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例1: 输入:matrix [[1,2,3],[4,5,6],[7…
【Matlab MDVRP】遗传算法求解多仓库车辆路径规划问题【含源码 1481期】
一、代码运行视频(哔哩哔哩)
【Matlab MDVRP】遗传算法求解多仓库车辆路径规划问题【含源码 1481期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]张露.基于改进遗传算法求解带时间窗车辆路径规划问题[J].中国物流与采购. 2020,(14…
三对角矩阵解算——TDMA解法(C++)
做三次样条曲线时,需要解三对角矩阵(Tridiagonal Matrices)。常用解法为Thomas Algorithm,又叫The tridiagonal matrix algorithm (TDMA)。它是一种基于高斯消元法的算法, 分为两个阶段:向前消元forward el…
面试题29:顺时针打印矩阵
面试题29:顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {if(matrix.empty())return {};vector<int> …
关于机器人状态估计(13)-线性代数有多重要?18.06总结
太久没更新主要是在忙开发和测试,这几个月被很多同学提问,同时接触了一些实习生。普遍发现动手能力不错,数学基础却差异很大。从我身边电子,CV或者SLAM做得比较杰出的朋友来看,大家普遍有个共性,具备优秀或…
Law of total expectation證明
Law of total expectation證明Law of total expectation的公式為: E(X)E(E(X∣Y))\operatorname{E} (X) \operatorname{E} \left( \operatorname{E} (X \mid Y) \right)E(X)E(E(X∣Y))
參考Law of total expectation - Proof in the finite and countable c…
leetcode[537]复数乘法 python3实现(简单模拟,map函数的应用)
# 复数 可以用字符串表示,遵循 "实部虚部i" 的形式,并满足下述条件:
#
#
# 实部 是一个整数,取值范围是 [-100, 100]
# 虚部 也是一个整数,取值范围是 [-100, 100]
# i -1
#
#
# 给你两个字符…
Leetcode-D44-数组-48. 旋转图像54. 螺旋矩阵(明天复习)
一、复习
1、47. 全排列 II 写的还不错,思路大体上对,就是还是小小的调试了一下——当size0的时候,是进不去for循环的,所以需要在size1的时候就判断,然后直接append(path),然后retu…
【算法设计与分析qwl】02-06递归树
递归树概念:——迭代的图形表述。
迭代在递归树的表示: 二层子树例子: 递归树生成规则: 实例1: 对递归树上的量求和: 实例2: 右边路径比左边长,可能左边已经不存在了,…
Leetcode-D47-数组-74. 搜索二维矩阵
这两天又因为一些事情,没有更新,要继续啦~
一、复习
73、矩阵置零
刚开始有个大错误,就是在更新的时候,直接把记录着info的第一行/第一列更新了。这是不对的,相当于把信息抹去了。应该先扫描一遍第一行&第一列&…
n阶行列式如何求解?
证明题
优先考虑数学归纳法,一类偏多:
计算题
递推法(先求DnxxDn-1,再用Dn的公式代入Dn-1,一层一层拨开,注意Dn-1是右下还是左上,矩阵性质不能变)直接计算法(直接计算…
JZ12 矩阵中的路径
剑指Offer编程链接:JZ12
题目描述: 思路:递归回溯的方法,总结一下什么情况需要使用递归:
递归在解决问题时,通常涉及以下情况:
问题可被分解为较小的相似子问题。子问题与原问题具有相同的结…
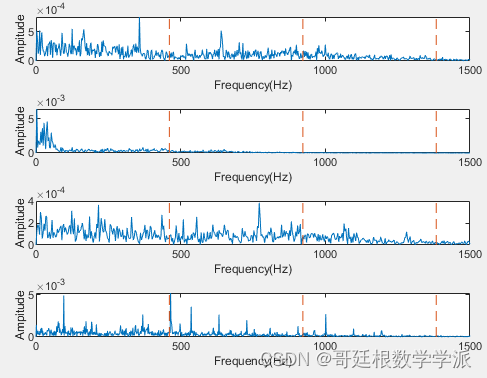
音乐处理原理第二章:信号傅里叶分析-补充
一些练习 采样频率Fs1/采样周期T采样频率F_s 1/采样周期T采样频率Fs1/采样周期T 计算以下STFT的时间分辨率,频率分辨率和那奎斯特频率 Fs22050Hz,N1024,H512F_s22050\mathrm{Hz}, N 1024, H 512Fs22050Hz,N1024,H512Fs48000Hz,N1024,H256F_s 48000\mathrm{H…
labview和matlab求解方程组
用labview和matlab求解一个方程组
x1x2x36
4x2-x35
2x1-2x2x31
求解X1,X2,X3. matlab求解如上图 labview求解如上图,在数学运算方面,labview更加直观感觉。
矩阵求导中的分子布局和分母布局
1.求偏导的自变量的符号区别
使用标量、向量和矩阵总共有九种可能性。请注意,当我们考虑每个自变量和因变量中更多数量的分量时,我们可能会留下非常多的可能性。下表收集了最能以矩阵形式最整齐地组织的六种导数。
在这里,我们使用了最一般…
数学建模算法一之层次分析法
数学建模算法一之层次分析法
数学建模算法一之层次分析法
方法1:算术平均法求权重 如何改变文本的样式
强调文本 强调文本
加粗文本 加粗文本
标记文本
删除文本 引用文本 H2O is是液体。
210 运算结果是 1024.
插入链接与图片
链接: link.
图片: Alt
带…
线性代数分块矩阵求逆矩阵_矩阵的调用列 使用Python的线性代数
线性代数分块矩阵求逆矩阵Linear algebra is the branch of mathematics concerning linear equations by using vector spaces and through matrices. Matrix is the key to linear algebra. All the linear algebra revolves around matrices. Columns are the heart of a Ma…
MATLAB隐函数绘图 使用隐函数作二维图 使用隐函数作三维图
如果给定了函数的显示式,可以先设置自变量向量,然后根据表达式计算出函数向量,从而用plot等函数绘制出图形,但如果函数用隐函数形式给出,则很难用上诉方法绘制图形。
使用隐函数作二维图
绘图函数:ezplo…
数学建模第一天:数学建模工具课之MATLAB的入门
目录
一、MATLAB的简介
二、Matlab基础知识
1. 变量
①命名规则
②特殊变量名
2、数学符号与函数调用
①符号
②数学函数
③自定义函数
三、数组与矩阵
1、数组
①创建数组
②访问数组元素
③数组运算
2、矩阵
①定义
②特殊矩阵
③矩阵运算
四、控制流
…
ML算法——线代预备知识随笔【机器学习】
文章目录 数学预备知识3、线性代数3.1、矩阵奇异值分解(SVD)3.2、广义逆矩阵(Moore-Penrose )3.3、数据白化(Data Whitening)3.4、向量导数 4、其它 数学预备知识
3、线性代数
3.1、矩阵奇异值分解&#…
Matlab入门1(有手就行)
目录 1.认识matlab(粗略)
2.matlab的计算器功能(当然大材小用了) 3.建立matlab项目: 4.matlab变量命名规则
5.清空环境变量
6.注释
7.matlab数据类型
(1)数字:
(2)字符与字符串…
线性代数的学习和整理17:向量空间的基,自然基,基变换等(未完成)
目录 3 向量空间的基:矩阵的基础/轴
3.1 从颜色RGB说起
3.2 附属知识
3.3 什么样的向量可以做基?
3.4 基的分类
3.1.1 不同空间的基---向量组的数量可能不同
3.1.2 自然基
3.1.3 正交基
3.1.4 标准正交基
3.1.5 基和向量/矩阵
3.1.6 基变换
…
POE指数积公式的简单matlab实现
参考现代机器人学 及机器人工程师进阶之路(八)指数积(PoE)建立机械臂模型及正运动 1.使用Robotics在matlab中建立一个简单的机械臂,方便验证后面的代码写的对不对
%Robotics 工具箱介绍: https://blog.csd…
MATLAB科学计算04(线性代数问题求解一)
文章目录特殊矩阵矩阵的基本概念求解线性方程组直接求解判定求解特殊矩阵
零矩阵、1矩阵及单位矩阵
生成nxn方阵:Azeros(n), Bones(n), Ceye(n)生成mxn矩阵:Azeros(m,n), Bones(m,n), Ceye(m,n)生成和矩阵B同样位数的矩阵:Azeros(size(B)…
20230702 正态分布的几个性质
正态分布以及高斯函数的定义
如果随机变量 X X X 的密度函数为 f μ , σ ( x ) 1 σ 2 π e − ( x − μ ) 2 2 σ 2 , x ∈ R , σ > 0 f_{\mu, \sigma}(x)\frac{1}{\sigma \sqrt{2 \pi}} e^{-\dfrac{(x-\mu)^2}{2 \sigma^2}}, \quad x \in \mathbb{R}, \sigma>0 …
【GNN】谱域图卷积
谱域图卷积
1. 谱域卷积的背景知识
1.1 谱域图卷积实现思路 f 1 ( t ) ⋆ f 2 ( t ) F − 1 [ F 1 ( w ) F 2 ( w ) ] f_1(t) \star f_2(t) F^{-1}[F_1(w)F_2(w) ] f1(t)⋆f2(t)F−1[F1(w)F2(w)]
1.2 如何定义图上的傅里叶变换
经典傅里叶变换: x ( …
正交变换最强总结笔记,解决每一个考研线代人的理解难关
所有学线代的人都必须透彻理解和应用正交变换。 正交变换图形上最直观的作用是:一巴掌把歪七扭八的图形打正,如下:
而图形立正后,表达式也随之立正,xixj{x_{i}x_{j}}xixj群魔退散,平方项真身显现&…
stl向量_在C ++ STL中更改向量的特定元素
stl向量Given a C STL vector and we have to change a particular element. 给定一个C STL向量,我们必须更改一个特定元素。 更改向量的特定元素 (Changing a particular element of a vector ) We can change a particular element of a C STL vector using fo…
第七章,相似矩阵及其应用,5-正定二次型
第七章,相似矩阵及其应用,5-正定二次型 惯性定理定理(惯性定理) 正(负)定二次型定义判定标准形系数判别法顺次主子式判别法 应用示例 玩转线性代数系列的最后一篇:
玩转线性代数(40)正定二次型…
Eigen库的基本使用说明(二)
之前的文章中,简单的介绍了一些基本的操作,回归之前的内容可以参考一下链接:
zEigen库的基本使用说明_每日亿学的博客-CSDN博客_eigen库 本章内容主要就是继续延伸Eigen库的使用内容也会实时进行更新,Eigen库在SLAM中使用广泛&am…
视觉SLAM十四讲 ch3 (三维空间刚体运动)笔记
本讲目标
●理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。 ●学握Eigen库的矩阵、几何模块使用方法。
旋转矩阵、变换矩阵 向量外积
向量外积(又称叉积或向量积)是一种重要的向量运算,它表示两个向量所形成的平行…
独立成分分析ICA/FastICA
最近在学习CSP,然后又注意到了ICA,这个算法之前就用过,但是没有系统的整理一下,所以就在这里梳理一下相关内容,方便以后查阅。 独立成分分析ICA/FastICA1 盲源分离(BlindSource Separation,BSS&…
《机器学习线性代数基础:Python语言描述》读书笔记----矩阵与空间映射
矩阵其实描述了空间中的映射
矩阵与空间映射
由于矩阵乘法的作用,原始向量的空间位置甚至其所在空间的维度和形状都发生了改变,这便是矩阵乘法的空间映射作用。 Ax[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn][x1x2⋮xn][a11x1a12x2⋯a1nxna21x1a22x2…
kubernetes学习笔记整理集合
大佬整理的: 可以直接看这个就行了:yooome/LearningNotes
--------
k8s-扫盲系列-01_u010953880的专栏-CSDN博客
kubernetes-扫盲系列-02_u010953880的专栏-CSDN博客
kubernetes-01-集群搭建-01-环境准备_u010953880的专栏-CSDN博客
kubernetes-01-…
Generalized-ICP(GICP)論文研讀
Generalized-ICP論文研讀前言損失函數推導應用point-to-pointpoint-to-planeplane-to-plane前言
ICP最基本的形式是point-to-point,即以點到點之間的距離作為損失函數;它的一個變種是point-to-plane,改用點到目標點局部擬合平面的距離作為損…
ICP(Iterative Closest Point)算法推導
ICP(Iterative Closest Point)算法推導前言算法流程損失函數求解t化簡令導數為0求解R回代t將f轉化為x^2^y^2^-2xy的形式化簡並引入去除均值的點雲SVD矩陣分解尋找最優的R前言
本篇整理自深藍學院三維點雲處理課程的Lecture 9 – Registration。推導過程…
Frobenius norm的特性以及證明
Frobenius norm的特性以及證明前言Frobenius norm性質一證明性質二證明Frobenius inner product證明Frobenius decomposition證明前言
本篇整理自深藍學院三維點雲處理課程的Lecture 9 – Registration,並補上證明。
Frobenius norm ∥A∥F≜∑i1m∑i1n∣Aij∣2tr…
由旋轉矩陣得到旋轉軸和旋轉角度
由旋轉矩陣得到旋轉軸和旋轉角度前言旋轉軸旋轉角度前言
羅德里格公式闡述了旋轉矩陣RRR和旋轉軸nnn及旋轉角度θ\thetaθ之間的關係:R(n,θ)Isin(θ)n(1−cos(θ))n2R(n, \theta) I \sin(\theta)n^{\times} (1-\cos(\theta)){n^{\times}}^2R(n,θ)Isin(θ)…
ACM训练赛赛后补题:Happy Necklace(思维+递推+矩阵快速幂)
题目描述: 分析
这道题很容易就可以定性为动态规划,需要能够推出递推公式;然后观察发现n太大了,最多只能接收O(logn)的复杂度,这样的复杂度,实现的方式就是矩阵快速幂。 首先题目所说的是这一串项链里面…
對極幾何基礎矩陣求解 - 七點法
對極幾何基礎矩陣求解 - 七點法前言基礎矩陣基礎矩陣求解方法七點法推導參考連結前言
一個三維點xxx在兩個相機中的投影分別為x1x_1x1及x2x_2x2,這兩個投影點座標需滿足"對極約束",即x2TFx10x_2^TFx_1 0x2TFx10。其中的FFF即為基礎矩…
线性代数(第六版)同济大学 习题一 (7-9题)个人解答
线性代数(第六版)同济大学 习题一(7-9题) 7.设n阶行列式Ddet(aij),把D上下翻转、或逆时针旋转90∘、或依副对角线翻转、依次得D1∣an1⋅⋅⋅ann⋮⋮a11⋅⋅⋅a1n∣,D2∣a1n⋅⋅⋅ann⋮⋮a11⋅⋅⋅an1∣&…
短视频抖音账号矩阵系统源码开发者自研(三)
一、站在开发者角度布局开发本套体系系统
开发技术新的方向。通过持续的技术创新和用户需求分析,我们将更加注重个性化开发本套短视频矩阵源码系统,目前市面上涵盖的基本功能有视频剪辑、绑定发布、智能回复、数据统计等一些基本的功能。此外我们在开发…
线性代数(第六版)同济大学 习题一 (1-4题)个人解答
线性代数(第六版)同济大学 习题一(1-4题) 1.利用对角线法则计算下列三阶行列式:\begin{aligned}&1. \ 利用对角线法则计算下列三阶行列式:&\end{aligned}1. 利用对角线法则计算下列三阶行列式&am…
【Matlab路径规划】改进的遗传算法机器人避障路径规划【含GUI源码 703期】
一、代码运行视频(哔哩哔哩)
【Matlab路径规划】改进的遗传算法机器人避障路径规划【含GUI源码 703期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)…
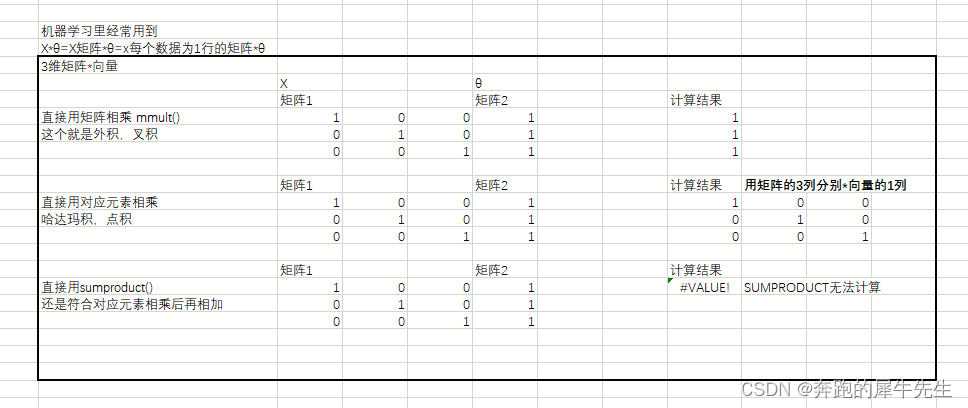
向量的内积外积哈达玛积
1.向量的内积
1.1 定义
从代数角度看,先对两个数字序列中的每组对应元素求积,再对所有积求和,结果即为点积。从几何角度看,点积则是两个向量的长度与它们夹角余弦的积。
表示形式:ATBA^TBATB、<A,B><A,B&g…
(邱维声)高等代数课程笔记:行列式按一行(列)展开
行列式按一行(列)展开
例题 1:一般地,设 ∣A∣|A|∣A∣ 是一个三阶行列式,则有 ∣A∣∣a11a12a13a21a22a23a31a32a33∣a11a22a33a12a23a31a13a21a32−a13a22a31−a12a21a33−a11a23a32a11(a22a23−a23a32)−a21(a12a3…
如何判断n(n-1)/2的奇偶性【数学问题】
这道题是我复习线性代数时遇到,个人觉得很有意思,所以拿出来分享一下思路。 首先,不管n是奇数还是偶数,那么n-1的奇偶性肯定与n相反,那么对于n(n-1)/2来说,也就是一个奇数乘以(偶数除以2&#x…
《程序设计基础》 第七章 数组 7-10 求矩阵的局部极大值 (15 分)
给定M行N列的整数矩阵A,如果A的非边界元素A[i][j]大于相邻的上下左右4个元素,那么就称元素A[i][j]是矩阵的局部极大值。本题要求给定矩阵的全部局部极大值及其所在的位置。
输入格式:
输入在第一行中给出矩阵A的行数M和列数N(3≤…
凸优化及拉格朗日对偶问题
只记录机器学习方法中需要用到的最优化知识,不做系统总结,持续更新ing。 文章目录1 凸优化1、凸集2、凸性条件3、凸规划4、凸规划性质5、凸优化问题2 拉格朗日函数及其对偶问题1、拉格朗日函数(含KKT条件)2、拉格朗日对偶问题1 凸…
使用奇异值分解(SVD)并随机选取特征值进行图像处理(附python源码)
目录1.前言2.准备3.奇异值分解(含源码)3.1过程3.2结果3.3奇异值分解对非正方形图片的处理实例4.参考资料1.前言
因为python的特征值分解存在复数矩阵的情况,而后续步骤不能很好的兼容复数,于是采用了范围更广的奇异值分解(SVD)进…
协同过滤的进化--矩阵分解算法(MF)
一: MF基础知识
线性代数,机器学习,梯度下降等内容需要各位看官在了解本文之前进行一定基础学习。MF解决的主要问题在两点,这两点也是协同过滤的主要缺点,第一是协同过滤处理稀疏矩阵的能力较弱(共现矩阵稀…
【Matlab】求解非线性方程组Ax=b的一个特解中,x=A\b是怎么来的?
求解非线性方程组Axb的一个特解中,xA\b是怎么来的?
一、刚开始学习时,对 \ 这个符号不理解,我记得高数里面求特解是要写一堆东西的,后来翻看了一些matlab视频,最后才将其搞懂!其实 \ 就是一个…
计算方法 8.常微分方程
常微分方程是干嘛的?: 先学习基本概念: 解析法当然是有的,但我们不用。我们把微分方程改成成差分方程,这样好算。 现在我们来学习具体方法: h就是xn1-xn。 由于泰勒展开只占了一项,相当于把一小…
算法学习(十八)——Actor Critic
理论上的解释: 强化学习(Reinforcement learning)中Actor-Critic算法该如何深入理解? - 白辰甲的回答 - 知乎 https://www.zhihu.com/question/56692640/answer/289913574 简单解释一下就是:以Policy Gradient算法族中…
图形学中常见的数学困惑
文章目录前言左右手系与旋转方向旋转矩阵为什么单单绕y轴是反的旋转矩阵的另推先旋转再平移和先平移再旋转旋转的两种视角欧拉角内旋、外旋与万向节死锁参考前言
我高中搞了三年数学竞赛,之前还对自己的数学能力很自负,现在发现自己太naive了。在学习图…
数据结构——时间复杂度
时间复杂度一、常见的时间复杂度二、时间复杂度的计算过程中的忽略原则三、时间复杂度大O记法四、时间复杂度分析1、加法法则2、乘法法则3、除法法则和减法法则四、图形分析一、常见的时间复杂度
# 常量阶O(1)# 对数阶O(logn)# 线性阶O(n)# 线性对数阶O(nlogn)# 平方阶,立方阶…
算法公式推导——PCA
文章目录1,算法定义2,算法步骤附录前言:关于主成分分析(Principle Component Analysis,PCA)的算法公式推导,文中若有写的不对的地方或者没写明白的地方,欢迎读者提出并交流。1&#…
【LeetCode54螺旋矩阵、LeetCode59螺旋矩阵II:简单模拟(Java实现,一种思想解决两道题)】
螺旋矩阵零、算法流程0.基本对比1.LeetCode59算法流程2.LeetCode54算法流程一.LeetCode59:螺旋矩阵II1)题目内容2)样例3)核心代码二.LeetCode54:螺旋矩阵1)题目内容2)样例3)核心代码…
矩阵分析学习笔记(四):λ矩阵及其Smith标准型
文章目录写在前面λ\lambdaλ矩阵及其Smith标准型多项式矩阵多项式矩阵的秩单位模阵多项式矩阵的逆一般情况下会是有理分式矩阵单位模阵的行列式刻画多项式矩阵的三种初等行(列)变换多项式矩阵的等价用初等变换将左上角降次多项式矩阵的Smith标准型Smith…
考研:研究生考试(五天学完)之《线性代数与空间解析几何》研究生学霸重点知识点总结之第七课二次型
考研:研究生考试(五天学完)之《线性代数与空间解析几何》研究生学霸重点知识点总结之第七课二次型 目录
7 二次型
7.1、知识点
7.1.1、二次型
7.1.2、矩阵的合同
优化理论12---- 既约梯度法
💖💖感谢各位观看这篇文章,💖💖点赞💖💖、收藏💖💖、你的支持是我前进的动力!💖💖 💖💖感谢你的阅读💖,专栏文章💖持续更新!💖关注不迷路!!💖 优化理论12---- Rosen的梯度投影法 、投影矩阵
优化理论12---- 既约梯度法
既约梯度法 文章…
向量,标量对向量求导数
1.已知 对谁求导数,就以谁(分母)作为主序,得出结果。比如这里x是列向量,求Ax关于x求导数,那么对x的每个分量分别求偏导数(写成一行),然后整理排成一列(同x一样是列向量)。…
三维重建基础与极几何
蓝色 紫色 红色
写在前面:本篇Blog仅作为学习笔记,学习内容来自于北邮CV-XUEBA团队的三维重建(精简版,鲁鹏)课程。
三维重建基础 三维重建总结
主要涉及以下几个关键问题:
解决第三个关键问题(对应关系)的方法 极几何
极几何…
L1,L2范数学习笔记
L1范数
作用:使解变为一个稀疏解,降低过拟合。
为什么会参产生稀疏解参考https://zhuanlan.zhihu.com/p/129024068 因为在0处可能是极小点(可能性受惩罚系数影响),因此容易收敛到极小点,也就是0处&#x…
2刷第二天(LeetCode977. 有序数组的平方、LeetCode209. 长度最小的子数组、LeetCode59. 螺旋矩阵 II)
一.有序数组的平方: 题目链接:给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
解法: 1.本题首先的想法就是都给它平方了,然后调用sort方法,但是…
事件响应必备:DNS攻击与防御矩阵
攻击者采用了哪些DNS攻击技术,哪些组织可以帮助事件响应团队检测、缓解和预防这些技术?FIRST近日发布的DNS攻击与防御矩阵提供了答案。
DNS作为互联网基础架构的一项核心服务,安全问题严峻,各种攻击层出不穷。F5发布的数据显示&a…
【AI绘图学习笔记】奇异值分解(SVD)、主成分分析(PCA)
这节的内容需要一些线性代数基础知识,如果你没听懂本文在讲什么,强烈建议你学习【官方双语/合集】线性代数的本质 - 系列合集 文章目录奇异值分解线性变换特征值和特征向量的几何意义什么是奇异值分解?公式推导SVD推广到任意大小矩阵如何求SV…
(邱维声)高等代数课程笔记:矩阵的加法、数量乘法与乘法
(邱维声)高等代数课程笔记:矩阵的加法,数量乘法与乘法 \quad前面已经看到,矩阵的初等行变换、矩阵的秩 在线性方程组理论中起着非常重要的作用,因此,系统地研究一下矩阵是非常有必要的。 \quad本…
python矩阵乘法全面解读,python矩阵乘法常用代码
矩阵乘法,顾名思义是矩阵的乘法,矩阵相乘的含义是两个向量的积,在 Python中一般以乘号或括号表示。与常用的加、减、乘、除运算不同,矩阵乘法只能用于对给定矩阵进行乘法运算,不能进行除法运算。若要计算矩阵乘法的值&…
DFIG控制10: 双馈发电机的动态模型
DFIG控制10: 双馈发电机的动态模型。主要介绍DFIG在三相坐标系、定子αβ坐标系、dq同步坐标系下的模型。
本文主要是整理了DFIG的动态模型的公式和坐标变换的过程。某些描述是为了便于自己理解,不一定准确。
大部分内容参考: G. Abad, J. …
数学基础|线性代数回顾
因为学机器学习的时候发现自己线性代数忘光光了(悲😓,本篇捞一捞当年学线性代数看哔哩哔哩宋浩老师补充记的潦草笔记。 目录
📚线性代数知识点
🐇向量
🥕向量的线性组合
🥕线性相关无关的性…
【图形学数学基础】行列式几何
行列式的几何解释
矩阵的行列式可以把每一行当做一个矢量,例如: [2.330.670.672.00]\left[ \begin{array}{c c} 2.33&0.67 \\ 0.67 &2.00 \end{array} \right] [2.330.670.672.00] 第一个向量是 (2.33, 0.67) 第二个…
MATLAB 之 数值数据,矩阵的表示和变量及其操作
文章目录 一、数值数据1. 数值数据类型的分类1.1 整型1.2 浮点型1.3 复型 2. 数据的输出格式 二、矩阵的表示1. 矩阵的建立1.1 直接输入法建立矩阵1.2 已建好的矩阵建立更大的矩阵 2. 冒号表达式3. 矩阵元素的引用3.1 矩阵元素的引用方式3.2 利用冒号表达式获得子矩阵3.3 利用空…
克拉默法则证明(Cramer‘s Rule)
若 n 个方程 n 个未知量构成的非齐次线性方程组: { a 11 x 1 a 12 x 2 . . . a 1 n x n b 1 a 21 x 1 a 22 x 2 . . . a 2 n x n b 2 . . . . . . a n 1 x 1 a n 2 x 2 . . . a n n x n b n \begin{equation*} \begin{cases} a_{11}x_{1} a_ {12}x_{2}…
抖音矩阵系统源码开发技术分析
在这个过程中,开发人员使用了多种编程语言、框架和工具,包括 Python、Java、Hadoop、Spark 和 Kafka 等。他们还使用了不同的数据库技术,例如 MySQL 和 MongoDB。 整个开发过程通常分为四个主要阶段:需求分析、设计、开发和测试。…
卓越讲坛:指标定理简介
卓越讲坛:指标定理简介
学习过程
刘博教授在提及 A t i y a − S i n g e r Atiya-Singer Atiya−Singer 指标定理前,先从拓扑、几何和复分析的三个现代理论成果开始引入。
先从3维空间中的2维曲面,例如球面、环面等开始谈起:…
机器学习-线性代数-解方程组
解方程组 文章目录 解方程组一、从空间映射的角度研究方程组二、方程解的个数1. r m n2. r n < m3. r m < n4. r < m 且 r < n 三、方程组解求法 一、从空间映射的角度研究方程组
对于如下方程组: a 11 x 1 a 12 x 2 . . . a 1 n x n b 1 a 21…
C#,码海拾贝(41)——求解“线性最小二乘问题”的“广义逆法”之C#源代码
using System;
namespace Zhou.CSharp.Algorithm { /// <summary> /// 求解线性方程组的类 LEquations /// 原作 周长发 /// 改编 深度混淆 /// </summary> public static partial class LEquations { /// <summary> /…
[HNOI2011]数学作业 题解
[HNOI2011]数学作业[HNOI2011]数学作业。 直接考虑 Dp\tt DpDp 显然 fifi−110xif_i f_{i - 1} \times 10^{x} ififi−110xi。那么我们直接将其分段进行计算即可。
具体的矩阵: [1ifi]\left[ \begin{matrix} 1 & i & f_i \end{matrix} \right] [1i…
抖音账号矩阵系统源码开发怎么用
以下是一些关键的技术交付形式:
1. 形成完整的运营需求框架 在开展任何项目前,首先应建立一个完整的运营需求框架。这个框架要对于整个系统的功能、结构、性能、安全、稳定性等方面进行详细的需求分析。并且需要与各方沟通,形成清晰的需求文…
Rotation-Invariant-Distributions浅析
文章目录定义举例说明总结定义
这里给出旋转不变分布(Rotation-Invariant-Distributions)的两个定义
第一个定义 这里的旋转矩阵R\pmb RRRR就是正交阵。该定义比较直接,也比较形象。
第二个定义 该定义所述的spherically symmetric就是指旋转不变,上…
[LeetCode]01.07 旋转矩阵
旋转矩阵
给你一幅由 N N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
示例 1:
给定 matrix
[[1,2,3],[4,5,6],[7,8,9]
],原地旋转输入矩阵,使其变为:…
羅德里格斯公式的證明
羅德里格斯公式的證明設旋轉向量長度為θ\thetaθ,⽅向為nnn,那麽旋轉矩陣RRR為: RcosθI(1−cosθ)nnTsinθn^R \cos\theta I (1 - \cos\theta)nn^T \sin\theta n\hat{}RcosθI(1−cosθ)nnTsinθn^
參考Rodrigues’ rotation for…
深度学习——基础知识:微分
文章目录一. 导数和微分二. 偏导数三. 梯度三. 链式法则一. 导数和微分
在深度学习中,对于每个参数, 如果我们把这个参数增加或减少一个无穷小的量,我们可以知道损失会以多快的速度增加或减少。 定义 uf(x)3x^2−4x
import numpy as np
imp…
深度学习——基础知识:线性代数
文章目录一.标量、向量、矩阵1.标量2.向量3. 矩阵二. 张量及其算法性质三. 降维及非降维求和1.降维2.非降维求和四. 矩阵乘法1.点积2. 向量积3.矩阵乘法五. 范数一.标量、向量、矩阵
1.标量
标量由只有一个元素的张量表示。
import torchx torch.tensor([3.0])
y torch.te…
【Matlab WSN定位】磷虾群算法求解WSN定位优化问题【含源码 448期】
一、代码运行视频(哔哩哔哩)
【Matlab WSN定位】磷虾群算法求解WSN定位优化问题【含源码 448期】
二、 磷虾群算法简介
通过研究南极磷虾觅食和生活习性的仿真模拟实验, 2012年Gandomi和Alavi提出了一种处理复杂优化问题的磷虾群算法。KH算法仍然属于…
GAMES101学习笔记(Lecture3-4)
该笔记基于闫令琪大神的GAMES101课程及课后作业总结而成
目录
仿射变换
mvp变换
正交投影
透射投影 three-dimensional Euclidean space 三维欧氏空间 在伸缩,旋转后, 发现无法通过同维度的矩阵体现平移, 所以引入齐次方程 为了不把"平移变换"当做整个体系中…
MATLAB - 旋度可视化
1、环流与旋度
1)环流
在矢量场中,任意取一闭合曲线 ,将矢量沿该曲线积分称之为环流。C∮lF⃗⋅dl⃗C\oint_{l}\vec F \cdot d \vec lC∮lF⋅dl可见:环流的大小与环面的方向有关。
2)环流面密度 rotnF⃗limΔ…
算法公式推导——ICP
文章目录1,算法输入2,目标函数3,理论推导步骤1:步骤2:步骤3:4,算法总结:5,附录:前言:点云配准中的迭代最近点(Iterative Closest Poin…
【Matlab三维路径规划】A_star算法无人机山地三维路径规划【含源码 266期】
一、代码运行视频(哔哩哔哩)
【Matlab三维路径规划】A_star算法无人机山地三维路径规划【含源码 266期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)…
《程序设计基础》 第七章 数组 7-37 方阵转置 (15 分)
本题要求编写程序,将一个给定的 nn 方阵转置(行列互换)后输出。
输入格式:
输入第一行给出一个正整数n(1≤n≤6)。随后n行,每行给出n个整数,其间以空格分隔。
输出格式:
输出转置后的n行n列…
【Matlab优化调度】遗传算法求解码头泊位分配调度优化问题【含源码 247期】
一、代码运行视频(哔哩哔哩)
【Matlab优化调度】遗传算法求解码头泊位分配调度优化问题【含源码 247期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]于敏.基于多目标遗传算法的集装箱泊位—岸桥分配优化研究[D]. 大连海事大学
扩展卡尔曼滤波(EKF)算法详细推导及仿真(Matlab)
前言 扩展卡尔曼滤波算法是解决非线性状态估计问题最为直接的一种处理方法,尽管EKF不是最精确的”最优“滤波器,但在过去的几十年成功地应用到许多非线性系统中。所以在学习非线性滤波问题时应该先从EKF开始。EKF算法是将非线性函数进行泰勒展开…
拉东(Radon)变换
1917年,Radon 变换被提出。例如一个三维物体,如果知道它在各个方向的平面投影,能不能推出它的精确形状,这个数学问题可以由拉东变换解决。
拉东变换 R n R^n Rn 上实值函数的拉东变换定义为 n - 1 n - 1 …
MATLAB学习笔记2:MATLAB基础知识(下)
阅读前请注意:
1. 该学习笔记是华中师范大学HelloWorld程序设计协会2021年寒假MATLAB培训的学习记录,是基于培训课堂内容的总结归纳、拓展阅读。博客内容由 K2SO4钾 撰写、编辑,发布于 K2SO4钾 的个人投稿与华中师范大学HelloWorld程序设计协…
MATLAB学习笔记5:绘图基础与数据可视化(上)
阅读前请注意:
1. 该学习笔记是华中师范大学HelloWorld程序设计协会2021年寒假MATLAB培训的学习记录,是基于培训课堂内容的总结归纳、拓展阅读。博客内容由 K2SO4钾 撰写、编辑,发布于 K2SO4钾 的个人投稿与华中师范大学HelloWorld程序设计协…
计算方法 7.数值积分计算方法
这一节我们来学习如何估算积分: 这个Ak的计算方法其实就是把1,x,x^2都带进去……
求积公式是怎么来的?: 这个就直接带公式。 既视感满满。 这波图穷匕见,先用插值法把f(x)换了,再求积分。换成多项式了我还不要用公式…
计算机组成原理:补码的乘法运算
首先与上次提到的原码的乘法做对比: 由于补码乘法的符号位也要加入运算,所以说最后还要再多来一次乘法。
结果的符号是通过计算天然地得到的。 例子: 因为多了一个辅助位,ACC和X也要加一位,这样正好可以用双符号位。 …
线性代数:线性方程求解、矩阵的逆、线性组合、线性独立
本文参考www.deeplearningbook.org一书第二章2.3 Identity and Inverse Matrices 2.4 Linear Dependence and Span
本文围绕线性方程求解依次介绍矩阵的逆、线性组合、线性独立等线性代数的基础知识点。
一、线性方程
本文主要围绕求解线性方程展开,我们先把线性…
线性代数Python计算:向量组线性相关的判断
对给定的mmm-维向量组 α1(a11a21⋮am1),α2(a12a22⋮am2),⋯,αn(a1na2n⋮amn)\boldsymbol{\alpha}_1\begin{pmatrix}a_{11}\\a_{21}\\\vdots\\a_{m1}\end{pmatrix},\boldsymbol{\alpha}_2\begin{pmatrix}a_{12}\\a_{22}\\\vdots\\a_{m2}\end{pmatrix},\cdots,\boldsymbol{\al…
python 实现三维向量之间的夹角
原理: 设 这里求出的两个夹角的取值范围为 [0, pi]。 代码 这里方便起见,计算n个3维向量与z坐标之间的夹角。代码如下 import numpy as npnormal1 np.ran…
算法刷题-数组-螺旋矩阵
59.螺旋矩阵
力扣题目链接
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
思路
这道题目可以说在面试中出现频率较高的题目&#x…
三维空间刚体运动之旋转矩阵与变换矩阵
1. 旋转矩阵 1.1 点、向量和坐标系
点:点是空间中的基本元素,没有长度,没有体积;
向量:把两个点连接起来,就构成了向量,向量可以看成从某点指向另一点的一个箭头;只有当我们指定这…
PCL点云处理之协方差矩阵的计算、归一化、解算(一百九十二)
2023.07.01 下半年开始了,祝大家一切顺利 PCL点云处理之协方差矩阵的计算、归一化、解算(一百九十二) 一、算法介绍二、实现过程1.协方差矩阵计算2.协方差矩阵归一化3.协方差矩阵解算二、具体实验1.完整代码2.结果展示一、算法介绍
这里主要实现三件事情, (1)协方差矩阵…
矩阵对角线元素的和:揭秘数学之美,解密矩阵的隐秘密码
本篇博客会讲解力扣“1572. 矩阵对角线元素的和”的解题思路,这是题目链接。 本题的思路是:主对角线的下标满足i j,副对角线的下标满足i j size - 1,故只需要使用i遍历每一行,把(i, i)和(i, size - i - 1)的元素求和…
Thin Plate Spline薄板样条
自变量 x [ x 1 , x 2 ] \mathbf{x}[x_1,x_2] x[x1,x2] 是2维空间中的一个点,函数值 y [ y 1 , y 2 ] \mathbf{y}[y_1,y_2] y[y1,y2]也是2维空间中的一点,并且都在笛卡尔坐标系下表示。已知存在K个控制点 c { c i 1 , c i 2 , i 1... K } …
Matlab操作(2):线性代数中求矩阵相关数据的高级方法
文章目录1.特征多项式2.特征值与特征向量3.若当标准型4.求解线性方程组5.常用函数汇总 (求逆,化简(高斯法),转置,求秩)6.其他高级函数1.特征多项式
poly(A),返回矩阵A的特征多项式的向量表示形式,例如:
&…
数学建模系列-评价模型(四)---主成分分析法
主成分分析法可以理解为层次分析法的一种衍生,是为了舍去无用或者效用较少的参数来达到拟合的目的,为了简化计算。
主成分与原始变量之间的关系: (1)主成分保留了原始变量绝大多数信息。
(2&#x…
数学建模系列-优化模型(二)---图论模型(三)
本文考虑的是自最费用最大流问题。
最大流问题的标号法: 1.对初始点找有裕量的下一跳,用深度优先一路走下去,一直到终点为止,那么取这条路最小的一段的裕量。当然裕量也包括反向可以减少的量。 2.将这个裕量更新到这条路经的每个…
C语言方式实现求矩阵最大值
题目描述:
给定一个仅包含0和1的N*N二维矩阵,请计算二维矩阵的最大值,计算规则如下:
每行元素按下标顺序组成一个二进制数(下标越大越排在低位),二进制数的值就是该行的值。矩阵各行值之和为矩…
[解题报告]【第35题】给定两个 a X b 和 c X d 的矩阵 ,求两个矩阵的乘积
全文目录🎁主要知识点矩阵乘法📓课后习题面试题 01.08. 零矩阵📑写在最后今天是c语言基础打卡的第35天,主要内容是矩阵的操作,希望大家能够理解呢,我就给大家记一下重点,给点课后题提示0.0。
相关链接&…
C++学习日记#1.1——四元一次方程组进行Sor松弛迭代法求解(现已推向n元一次方程组进行Sor松弛迭代法求解)
在这篇文章中,不会有太多的讲解,主要是因为Sor迭代法和高斯-赛德尔(gauss-seidle)迭代法的程序只有迭代公式的一点点区别,当松弛因子为1的时候,Sor迭代法和高斯-赛德尔(gauss-seidle)迭代法是一致的。
高斯-赛德尔(gauss-seidle)…
不选主元的Gauss消去法和列主元高斯消去法求解三对角矩阵
采用 MATLAB 语言不选主元和列主元 Gauss 消去法编写成通用的子程序;然后用编写的程序求解 下列84阶方程组。 问题描述:求解的所有步骤及程序请详细见数值线性代数\Linear Equation Direct Solution_1\Computer_problem1.m 这里仅说明伪代码算法和求解结…
线性代数 行矩阵的值_矩阵的最小值| 使用Python的线性代数
线性代数 行矩阵的值Prerequisites: 先决条件: Defining a Matrix 定义矩阵 Here, we are implementing a Python program to find the minimum value from a matrix or vector using an inbuilt function in the numpy library. 在这里,我们正在实现一…
Python中where()的用法
Python中where()的用法向量化运算,更容易提高计算速度
import numpy as np
#定义一个数组a
a np.array([8,2,7,5,1,4])
#print(a<5)的输出结果是“布尔值索引”:
print(a<5)[False True False False True True]print(a5)
[False False False …
Pyhton Numpy tile函数 行列复制
文章目录1. tile(matrix, (m, n))2. 对于向量同样成立1. tile(matrix, (m, n))
用法
将matrix矩阵行上复制m次,列上复制n次
>>> import numpy as np
>>> a np.mat([[1, 2], [3, 4]])
>>> b np.tile(a, (2, 2))
>>> b
matr…
来人!把朕的线性代数呈上来!
为啥讲数学?先说下一个时间线:无意间发现了一个宝藏up主3Blue1Brown[1]在看视频的时候,偶然发现一个集合:线性代数的本质。突然想起上学的时候矩阵论(线性代数)老师总说矩阵很优美,但我又一直没…
Python学习 Day72 numpy_IO操作
IO操作
numpy 可以读写磁盘上的文本数据或二进制数据
numpy 为 ndarray 对象引入了一个简单的文件格式:npy
npy 文件用于存储重建 ndarray 所需的数据、图形、dtype 和其他信息
常用IO函数作用load() 和 save()是读写文件数组数据的两个主要函数,默认…
Python学习 Day68 Ndarray数组属性 03
numpy数组的基本使用
一、numpy数组与Python中列表的对比
效率对比 二、Ndarray数组属性
NumPy 数组的维数称为秩(rank),一维数组的秩为 1,二维数组的秩为 2,以此类推
在 NumPy中,每一个线性的数组称为…
【Matlab优化预测】混沌粒子群算法优化极限学习机ELM预测【含源码 1586期】
一、代码运行视频(哔哩哔哩)
【Matlab优化预测】混沌粒子群算法优化极限学习机ELM预测【含源码 1586期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 1 matlab版本 2014a
2 参考文献 [1]王登辉.基于粒子群算法的极限学习机优化设计及…
【Matlab车间调度】改进蛙跳算法求解车间调度问题【含源码 073期】
一、代码运行视频(哔哩哔哩)
【Matlab车间调度】改进蛙跳算法求解车间调度问题【含源码 073期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子…
矩阵分解(2)--- 奇异值分解(SVD),AX=b问题
1. 特征值与特征向量 2. SVD奇异值分解
2.1 SVD定义
wiki: https://zh.wikipedia.org/wiki/%E5%A5%87%E5%BC%82%E5%80%BC%E5%88%86%E8%A7%A3 2.2 SVD理解
Ref:奇异值分解(SVD) - 知乎 应用: 对于齐次线性方程 A*X…
【Matlab车间调度】遗传算法求解柔性车间调度问题【含源码 660期】
一、代码运行视频(哔哩哔哩)
【Matlab车间调度】遗传算法求解柔性车间调度问题【含源码 660期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子…
[HNOI2002]公交车路线 题解
[HNOI2002]公交车路线[HNOI2002]公交车路线 这题和没有一样。 直接按照题意建立转移矩阵即可。
笔者的答案矩阵是: [fAfBfC…fH]\left[ \begin{matrix} f_{A} & f_B & f_C & \dots & f_H \end{matrix} \right] [fAfBfC…fH] 其中…
[SCOI2009]迷路 题解
[SCOI2009]迷路[SCOI2009]迷路 文章目录思考过程题解思考过程 这个东西发现距离只有 999,记得 Lcm(1…9)2520\tt Lcm(1 \dots 9) 2520Lcm(1…9)2520 那么直接考虑暴力处理出来,之后对于每个 TTT 进行分开计算即可。 显然这个很难写,但是同样…
关于 数学 线性代数
数学
听了大部分的数学通识课,觉得掌握主要的精髓思想,才是王道,而不是去纠结了大量的题目的计算,这样才不会考完试就忘。这是吴军传达的思想,也是今天看的一篇博客传达的思想。
线性代数
从文中抄到的一些总结&…
L0范数,L1范数,L2范数,Lp范数,无穷范数,Frobenius 范数表示意义
L0范数:是指向量中非0的元素的个数。
L1范数:是指向量中各个元素绝对值之和。
L2范数:是指向量各元素的平方和然后求平方根。
Lp范数: 是指向量各个元素绝对值p次方和的1/p次方。
无穷范数:是指向量中各个元素绝对值的最大值。…
基于遗传算法(GA)工具箱优化求解二元函数优化 -【 附代码+详细注解】
基于遗传算法工具箱求解二元函数优化 -【 附代码详细注解】一.优化函数二.优化后效果图三.完整代码前言: 链接: 遗传算法工具箱下载地址. 链接: 遗传算法工具箱的导入MatLab软件教程地址. 一.优化函数 求其最大值,求最小值只需在目标函数前加“-”负号即…
剑指offer 刷题 二十五 模拟(29 31)
文章目录剑指 Offer 29. 顺时针打印矩阵剑指 Offer 31. 栈的压入、弹出序列剑指 Offer 29. 顺时针打印矩阵 写了半天,终止条件写不对
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:def recur(matrix, row, col, li):for j in range(col):li.ap…
线性代数(Gilbert strang)笔记--第一章
UTF8gbsn
vector 对于向量vvv我们通常都是默认它为列向量。 数学上解决问题的步骤 建模(公式推导) 计算
Q:四维空间中的立方体,有多少个角?多少条边?多少个三维面? 0000→11110000\to11110000→1111,每一个二进制…
程序员的自我修养之数学基础10:超定方程的求解
超定方程
超定方程,即方程个数大于未知量个数的方程组(与之对应的,欠定方程是方程个数小于未知量个数的方程组)。前面说过了,线性方程组可以改写为矩阵的形式的形式。其中,是一个的系数矩阵,是…
矩阵的乘法,快速幂,转置
struct nn
{int a[5][5]; int n,m;
} ;矩阵相乘 由m行、n列的标量所构成的数组被称为一个m n的矩阵。一般用大写字母表示矩阵,对应的小写字母表示矩阵中的项。这里,aij就是矩阵A中第i行第j列的项。 定义矩阵A , B 。A和B可以作乘法操作当且仅当A的大小是…
C语言:L1-048 矩阵A乘以B (15 分)
文章目录一、题目二、方法11、思路2、代码一、题目 给定两个矩阵A和B,要求你计算它们的乘积矩阵AB。需要注意的是,只有规模匹配的矩阵才可以相乘。即若A有Ra行、Ca列,B有Rb行、Cb列,则只有Ca与Rb相等时,两个矩阵才能相…
【算法与数据结构】——前缀和,差分
参考博客二维差分 差分——(2)二维差分
前缀和
给定一个数组a,如果有一个数组p,p[i] p[i-1]a[i],这个数组p就是a的前缀和数组,p[b]就表示数组a的前b项和。p[b]-p[a-1]就表示数组a的[a,b]区间的和。
一维差分
给一…
特征值 是 系数行列式等于0时的 解
目录特征值与特征向量齐次线性方程组的解参考完特征值与特征向量
对nnn阶矩阵AAA,如果数λ\lambdaλ和nnn维非零列向量xxx使关系式 AxλxAx\lambda xAxλx 成立,那么,这样的数λ\lambdaλ称为矩阵AAA特征值,非零向量xxx称为AAA的…
线性代数Python计算:矩阵的2-维数组表示
用numpy包中的array类的2-维数组对象来表示矩阵,numpy包中含有大量的矩阵操作函数。 例1 用Python的numpy包提供的array对象表示矩阵、单位阵和零矩阵。
import numpy as np #导入numpy
Anp.array([[0,0,1,1,1,1,0,0], #生成88矩阵[0,1,0,0,0,0,1,0]…
线性代数学习笔记(二十五)——向量组的秩(二)
本篇笔记首介绍了矩阵的行秩和列秩,即矩阵的行秩等于矩阵的列秩等于矩阵的秩,而且矩阵乘积的秩不大于每个因子的秩;还介绍了求矩阵行秩和列秩的方法,即化为阶梯形矩阵;最后重点介绍了极大线性无关组的求法,…
线性代数学习笔记(二十二)——向量间的线性关系(二)
本篇笔记首先介绍了线性相关和线性无关的概念,关键是找到一组不全为零相关系数使得等成立;然后重点介绍了一些重要的结论,以及向量组线性相关和线性无关的几个充要条件。
1 线性相关与线性无关
线性相关:设α1,α2,...,αn\alph…
线性代数学习笔记(二十一)——向量间的线性关系(一)
本篇笔记首先介绍了线性组合,并给出了线性表示、线性表出和组合系数的概念;然后介绍了线性组合的相关性质,其中还介绍了单位向量组或基本单位向量组的定义,并将判断是否是线性组合转化为求方程组的解;最后介绍了向量组…
Leetcode 刷题必须Review 五 剑指offer(29 31 20)
文章目录剑指 Offer 29. 顺时针打印矩阵剑指 Offer 31. 栈的压入、弹出序列剑指 Offer 20. 表示数值的字符串剑指 Offer 29. 顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
class Solution:def spiralOrder(self, matrix: List…
凸优化基础学习——凸集
凸优化基础学习——凸集
文章内容全部来自对Stephen Boyd and Lieven vandenberghe的Convex Optimization的总结归纳。
电子书资源:
链接:https://pan.baidu.com/s/1dP5zI6h3BEyGRzSaJHSodg?pwd0000 提取码:0000
基本概念
仿射集合
**…
SVD奇异值分解相关技术
重要说明:本文从网上资料整理而来,仅记录博主学习相关知识点的过程,侵删。
一、参考资料
Eigen 矩阵的SVD分解
奇异值分解(SVD)
二、相关介绍
1. 单位阵
主对角线全为1的方阵,称为单位阵,…
[Eigen中文文档] 常见的陷阱
文档总目录 本文目录 针对模板方法的编译错误混叠对齐问题(运行时断言)C11 和 auto 关键字头文件问题(编译失败)三元运算符按值传递具有布尔系数的矩阵 英文原文(Common pitfalls)
针对模板方法的编译错误
详见[下一节](#8.9 C…
float的精度及其取值范围
float的存储方式
float在计算机中是用科学计数法的形式来存储的,科学计数法的表示方式是a.b*10^c,因为计算机中是用二进制来存储东西的,只有0和1这两个数,并且最大数为1,所以float的科学计数法为(-&#x…
07:矩阵归零消减序列和http://www.noi.openjudge.cn/
07:矩阵归零消减序列和
查看提交统计提问
总时间限制:
1000ms 内存限制:
65536kB
描述
给定一个n*n的矩阵(3 < n < 100,元素的值都是非负整数)。通过(n-1)次实施下述过程,可把这个矩阵转换成一个1*1的矩阵。每次的过…
矩阵特征值的求解过程
这几天一直在学习机器学习相关的算法,真心感受到了高数,概率论,线性代数用作用之大,也深深的感受到了自己当时学的太肤浅了,仅仅是为了考试而学习的。。。。。(如果有来生,没有来生了。。。。&a…
协同过滤算法—推荐系统基础算法(含python代码实现以及详细例子讲解)
推荐系统基础算法之协同过滤算法一、 算法简介1.1 算法概述1.2 算法核心和步骤二、基于用户的协同过滤算法(User-Based)2.1 相似度及预测值的计算2.1.1 相似度计算2.1.2 预测值的计算2.2 通过例子理解2.4 python代码实现三、基于物品的协同过滤算法&…
GLM 中的mat4
GLM 中的mat4
mat4中内存的排列方式
mat4的类定义在type_mat4x4.hpp中,下面是对整个类代码的部分截取:
struct tmat4x4
{typedef tvec4<T, P> col_type;private:col_type value[4];public:template <typename T, precision P>…
2023-8-15差分矩阵
题目链接:差分矩阵
#include <iostream>using namespace std;const int N 1010;int n, m, q;
int a[N][N], b[N][N];void insert(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] c;b[x1][y2 1] - c;b[x2 1][y1] - c;b[x2 1][y2 1] c;
}int main…
线性代数的学习和整理7:各种特殊矩阵(草稿-----未完成)
目录
1 单位矩阵
为什么单位矩阵I是 [1,0;0,1]T 而不是[1,1;1,1]T
2 旋转矩阵
3 伸缩矩阵 放大缩小倍数矩阵
4 镜像矩阵
5 剪切矩阵 矩阵
行向量
列向量 方阵 1 单位矩阵
[ 1 0 0 1]
为什么单位矩阵I是 [1,0;0,1]T 而不是[1,1;1,1]T
因为 矩阵 [1,0;0,1] 代表…
Leetcode237 删除链表中的节点
题目连接
请编写一个函数,用于 删除单链表中某个特定节点 。在设计函数时需要注意,你无法访问链表的头节点 head ,只能直接访问 要被删除的节点 。
题目数据保证需要删除的节点 不是末尾节点 。
代码
class Solution:def deleteNode(sel…
线性代数感悟之6 单位矩阵和初等矩阵
引言 最近在看 liuyubobobo 的 线性代数 课,感觉很妙,有些感悟记录一下~~~ 单位矩阵:
单位矩阵的特点:从左上角到右下角的对角线(称为主对角线)上的元素均为1。
使用行视角,将单位矩阵看…
阿里PEGASUS笔记:PEGASUS : Bridging Polynomial and Non-polynomial Evaluations in Homomorphic Encryption
文章目录PEGASUS : Bridging Polynomial and Non-polynomial Evaluations in Homomorphic Encryption摘要:引言:贡献:前序知识核心思路(将RLWE转换为FHEW,执行LUT,再转换回来)完整协议协议大纲S2C & ExtractKeySwi…
HoloLens MRTK模型切割算法解析
HoloLens MRTK模型切割算法解析脚本解析算法实现修改shader实现不同的功能修改Clipping Plane裁剪的范围修改模型透明度多个ClippingPrimitive对同一个模型进行切割Two different ClippingPrimitives clip a renderTwo of the same ClippingPrimitives clip a render脚本解析 例…
PTA 7-10 找鞍点 (20 分)
小染心得【暴力是无所不能的(时间超限当我没说)】
7-10 找鞍点 (20 分)
一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。
本题要求编写程序,求一个给定的n阶方阵的鞍点。
输入格式:
输入第一行给出…
线性代数感悟之3 矩阵列视角之矩阵表示空间
最近在看 liuyubobobo 的 线性代数 课,感觉很妙,有些感悟记录一下~~~
之前我一直都是行视角,原来还有个列视角!!! 矩阵和向量相乘的行视角: 矩阵和向量相乘的列视角: 和行视角一样…
Numpy的属性创建array矩阵的运算
import numpy as np#输入矩阵
array np.array([[1,2,3],[4,5,6],[7,8,9]])
print(array)print(array.ndim)
#查看矩阵的维度矩阵的运算
P4035 [JSOI2008]球形空间产生器 ——高斯消元
Link 一道高斯消元的题目,其实重点还是在如何得出方程组也就是增广矩阵。
代码
const double EPS1e-7;
inline int gauss(double a[][N], bool l[], double ans[], const int& n) {int res 0, r 0;for(int i 0; i < n; i)l[i] false;for(int i 0; i …
132-分割回文串 II
题目
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文。
返回符合要求的 最少分割次数 。
示例 1:
输入:s “aab” 输出:1 解释:只需一次分割就可将 s 分割成 [“aa”,“b”] 这样两个回…
【数理知识】向量的坐标基表示法,Matlab 代码验证
序号内容1【数理知识】向量的坐标基表示法,Matlab 代码验证2【数理知识】向量与基的内积,Matlab 代码验证 文章目录 1. 向量的坐标基表示2. 二维平面向量举例3. Matlab 代码验证Ref 1. 向量的坐标基表示
假设空间中存在一个向量 a ⃗ \vec{a} a &#…
线性代数的学习和整理12: 矩阵与行列式,计算上的差别对比
目录
1 行列式和矩阵的比较
2 简单总结矩阵与行列式的不同
3 加减乘除的不同
3.1 加法不同
3.2 减法不同
3.3 标量乘法/数乘
3.3.1 标准的数乘对比
3.3.2 其他数乘对比
3.4 乘法
4 初等线性变换的不同
4.1 对矩阵进行线性变换
4.2 对行列式进行线性变换呢…
Hadamard Product求导案例
1 问题
给定 x∈Rn1\mathbf{x} \in \mathbb{R}^{n \times 1}x∈Rn1,A∈Rnn\mathbf{A} \in \mathbb{R}^{n \times n}A∈Rnn,f(x)(Ax)⊙(Ax)\mathbf{f}(\mathbf{x})\sqrt{(\mathbf{A} \mathbf{x}) \odot (\mathbf{Ax})}f(x)(Ax)⊙(Ax)。 其中(⋅)\sqrt{…
矩阵内积求导/包含Hadamard root的矩阵求导/matrix elements-wise square root/矩阵逐元素平方根求导/F范数求导
包含Hadamard root的矩阵求导案例比较少,此案例仅供参考: 1 题目
给定 X∈Rn\mathbf{X} \in \mathbb{R}^{n}X∈Rn,A∈Rnn\mathbf{A} \in \mathbb{R}^{n \times n}A∈Rnn,f(X)∑i1n∣AX∣i2δ2f(\mathbf{X})\sum_{i\mathbf{1}}^{n…
LA@线性方程组@克拉默克拉姆Cramer法则
文章目录 preface线性方程组线性方程组的4个矩阵线性方程组的矩阵乘积形式线性表出形式齐次线性方程组非齐次线性方程组 相关的等价称呼👺相容性矩阵方程和线性方程组 Cramers Rule克莱姆法则对于非齐次方程组对于齐次方程组 Cramer法则的局限性证明Cramers Rule pr…
面试热题(螺旋矩阵)
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素 一看到这个大家有没有想到 就是一个螺旋形状,那这道题我们应该怎么解决? 我们先来仔细的看,它这种螺旋形状的遍历是先【右-下-左-上】…
斯坦福大学CS224d基础1:线性代数知识
作者:Zico Kolter (补充: Chuong Do) 时间:2016年6月翻译:MOLLY(mollyeclagmail.com) OWEN(owenj1989126.com)校正:寒小阳(hanxiaoyang.mlgmail.com) 龙心尘(johnn…
P1722 矩阵 II
题目背景
usqwedf 改编系列题。
题目描述
如果你在百忙之中抽空看题,请自动跳到第六行。
众所周知,在中国古代算筹中,红为正,黑为负……
给定一个12n 的矩阵(usqwedf:这不是一个 2n 的队列么ÿ…
【Unity SurfaceShader】学习笔记(八)光照模型
LitSphere(Matcap)
发光球体光照模型就是将发光球体的纹理映射在球体上,来实现光照效果。这可以创造一些效果细腻的发光球体效果,但是它不受光照影响,改变光照的方向,球体的光照效果不变。如果要在固定视角…
【Unity SurfaceShader】学习笔记(七)镜面反射
Unity内置的高光函数
Unity内置了一种高光光照模型——BlinnPhone。 使用方法如下:
Shader "Custom/BlinnPhong"{Properties {_MainTex ("Base (RGB)", 2D) "white" {}_MainTint ("Diffuse Tint", Color) (1,1,1,1)_Sp…
线性递推关系的求解方法
线性递推关系的求解方法定义常系数线性齐次递推关系的求解定义定理例题:Fibonacci数常系数线性非齐次递推关系的求解定理特解表例题定义
设kkk是给定的正整数,若数列f(0),f(1),…,f(n),…f(0),f(1),\ldots,f(n),\ldotsf(0),f(1),…,f(n),…的相邻k1k1k1…
VS2015+cublas实操记录(cuda加速GEMM矩阵乘加算子)
1. 环境配置:
cuda安装后一般的安装位置在:C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v11.8 把这个目录下的include和lib分别配置在vs中,安装cuda教程可参考:https://zhuanlan.zhihu.com/p/520995962(笔者…
R语言读取文件乱码的处理
文章目录R语言read.csv乱码问题UTF-8 BOM X.U.FEFFR语言read.csv乱码问题UTF-8 BOM X.U.FEFF
可参考: https://blog.csdn.net/ofoliao/article/details/106431217
其中需要注意的是,fileEncoding根据参数对整个文件的重新编码,encoding根据…
线性代数的学习和整理19,特征值,特征向量,以及引入的正交化矩阵概念(草稿)
目录
1 什么是特征值和特征向量?
1.1 特征值和特征向量这2个概念先放后
1.2 直观定义
1.3 严格定义
2 如何求特征值和特征向量
2.1 方法1:结合图形看,直观方法求
2.1.1 单位矩阵的特征值和特征向量
2.1.2 旋转矩阵
2.2 根据严格定义…
线性代数的本质(三)
文章目录 线性方程组高斯消元法初等行变换线性方程组的解向量方程齐次线性方程组的解非齐次线性方程组的解 线性方程组
高斯消元法
客观世界最简单的数量关系是均匀变化的关系。在均匀变化问题中,列出的方程组是一次方程组,我们称之为线性方程组(Linea…
【考研数学】线性代数第五章 —— 特征值和特征向量(1,理论背景与基本概念)
文章目录 引言一、特征值和特征向量的基本概念1.1 理论背景1.2 基本概念 写在最后 引言
特征值与特征向量是线性代数的重要内容,它的主要应用有:求矩阵的幂、矩阵的对角化、二次型的标准型。 一、特征值和特征向量的基本概念
1.1 理论背景
在一个多项…
【线性代数】沉浸式线性代数在线学习网站
地址:http://immersivemath.com/ila/index.html
这是全球第一本带交互式图形的线性代数教材,作者是 J. Strm, K. strm, and T. Akenine-Mller。
全书一共十章,各章节内容如下: 接下来我将对各章节进行简单的总结,另外…
【考研数学】线性代数第五章 —— 特征值和特征向量(2,特征值与特征向量的性质)
文章目录 引言二、特征值与特征向量的性质2.1 一般性质2.2 实对称矩阵特征值与特征向量的性质 写在最后 引言
承接前文,了解了一些基本概念后,我们来继续学习有关特征值和特征向量的内容。 二、特征值与特征向量的性质
2.1 一般性质
定理 1 —— 设 …
EKF之雅克比矩阵(一)
扩展卡尔曼滤波 (EKF)
EKF之雅克比矩阵 文章目录扩展卡尔曼滤波 (EKF)前言一、什么是线性化?二、雅克比矩阵1.矩阵的几何含义2.非线性矩阵与基底的关系3.雅克比矩阵三、工程中雅克比矩阵如何应用总结前言
一般的卡尔曼滤波(KF),…
pandas_计算最大回撤
目录
概念
一、数据为收盘价,计算最大回撤
二、数据为净值,计算最大回撤 概念 计算方法
1. 将收益率做成时间序列 2. 计算财富指数(也就是净值)【PS:初始净值为1】 3. 计算上一个最高点 4. 计算回撤率 5. 找出最大回撤
日期收益率财富指数(净值)上…
【李沐深度学习笔记】线性代数
课程地址和说明
数据预处理实现p3 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
线性代数
标量
标量(scalar),亦称“无向量”。有些物理量,只具有数值大小&…
数学基础--旋转矩阵的推导
1、简介
旋转矩阵的应用范围比较广,是姿态变换,坐标变换等的基础,由于考虑到IMU的融合需要用到旋转矩阵。因此,本文介绍一下旋转矩阵的推导过程。
2、推导过程
在介绍旋转矩阵之前,先介绍一下两个矩阵相乘的示意图如…
LCR 013. 二维区域和检索 - 矩阵不可变(java)
LCR 013. 二维区域和检索 - 矩阵不可变
题目
给定一个二维矩阵 matrix,以下类型的多个请求: 计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。 实现 NumMatrix 类: NumMatr…
debug过程中,矩阵左乘右乘相关概念梳理
1. 变换点或者变换向量
1.1左乘
矩阵左乘通常是指对”目标点“进行左乘,即: A ′ R ∗ A AR*A A′R∗A 其中,A为原始3维点,表示一个3*1的列向量,R为33的旋转矩阵,A‘为变换后的点 B ′ T ∗ B BT*B B′T∗B 其中…
二维数组中的查找(入门算法11)
题目:在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例: …
01 MIT线性代数-方程组的几何解释
一, 线性方程的几何图像 The geometry of linear equations
线性代数的基本问题就是解n元一次方程组
eg:二元一次方程组 矩阵形式: 系数矩阵(coefficient matrix): 未知数向量: 线性方程组简记为Axb
二, 行图像 Row Picture
行图像遵从解析几何的描述࿰…
矩阵求导的本质与分子布局、分母布局的本质
大佬讲解的实在太吊了。 就拿大佬的总结说明一下: 矩阵求导结果,无非就是分子的转置、向量化,分母的转置、向量化,它们的各种组合而已。 1、分子布局的本质:分子是标量、列向量、矩阵向量化后的列向量;分母…
是谁还没听过杨氏矩阵~原理和实现代码都已经准备好了
有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,请编写程序在这样的矩阵中查找某个数字是否存在。 要求:时间复杂度小于O(N); 看到这个题目时,我们会马上想到暴力求解,即遍历这个矩阵的每…
线性代数的学习和整理13: 函数与向量/矩阵
目录
1 函数与 向量/矩阵
2 函数的定义域,值域,到达域
3 对应关系 1 函数与 向量/矩阵
下面两者形式类似,本质也类似
函数的: axy ,常规函数里,a,x,y 一般都是单个数矩阵: AXY &a…
第六章,线性变换,2-线性变换的特征值与特征向量
第六章,线性变换,2-线性变换的特征值与特征向量 特征值与特征向量定义一般求法特征子空间性质 A − 1 、 A T 、 A ∗ A^{-1}、A^T、A^* A−1、AT、A∗的特征值和特征向量 A − 1 A^{-1} A−1 A T A^T AT A ∗ A^* A∗ 幂等矩阵、幂零矩阵的特征值和特征…
线性代数的学习和整理16:什么是各种空间(类型),向量空间,距离(类型)?
目录
1 空间相关的群,环,域,集合,空间的预备知识
1.1:群,环,域,集合,空间的定义(表示不懂,只是做个标记)
2 空间
2.1 各种空间概念…
线性代数的学习和整理18:什么是维度,什么是秩?关于秩的各种定理 (未完成)
目录
1 矩阵的秩
矩阵的秩
2 求秩的方法
矩阵的维度秩
矩阵的维度
向量的模,矩阵的模-没有把,难道是面积?
矩阵的平直概念
5 矩阵的初等变换(矩阵等价概念的引出) 0 问题引出:什么是秩?…
【理解线性代数】(四)线性运算的推广与矩阵基础
1. 数值加法和乘法
数值加法与乘法,是小学数学课程中的基本数学运算。例如: 加法:112 乘法:2*24 在这个知识层次下,运算的基本单位是数字。
2. 从数值到向量
数值加法,可以看作一维空间中的向量加法&…
矩阵快速幂及应用实战[C/C++]
矩阵快速幂 矩阵快速幂可以用来优化递推问题,如状态机DP,需要一丢丢线性代数里面矩阵的概念,只需要知道简单的矩阵乘法,结合我们普通的二分快速幂就能很快的掌握矩阵快速幂。 问题引入 三步问题。有个小孩正在上楼梯,楼…
4.矩阵的几何意义、变基与迹
文章目录 变基操作与矩阵矩阵的迹几何意义矩阵迹的几条性质 欢迎访问个人网络日志🌹🌹知行空间🌹🌹 变基操作与矩阵
我们知道空间中一点的坐标可以表示以原点为起点以该点为终点的向量。
以二维平面为例,如下图 选取…
14. 线性代数 - 线性方程组
文章目录 线性方程组矩阵行列式全排列和逆序数N阶行列式(非)齐次线性方程Hi,大家好。我是茶桁。 结束了「微积分」部分的学习之后我们稍作休整,今天正式开始另外一部分:「线性代数」的学习。小伙伴们放松完回来要开始紧张起来了。
我们之前说过,不管是哪一个工程学科,根…
线性代数(六)| 二次型 标准型转换 正定二次型 正定矩阵
文章目录 1. 二次型化为标准型1.1 正交变换法1.2 配方法 2 . 正定二次型与正定矩阵 1. 二次型化为标准型
和第五章有什么样的联系
首先上一章我们说过对于对称矩阵,一定存在一个正交矩阵Q,使得$Q^{-1}AQB $ B为对角矩阵
那么这一章中,我们…
向量的范数、矩阵的范数
向量的范数
p-范数 常用的0-范数、1-范数、2-范数、无穷-范数其实都是p-范数的特殊情形。
0-范数
当p0时,表示0-范数。它比较特殊,本质是一种计数,表示向量中非0元素的个数。
1-范数(也称L1范数)
当p1时ÿ…
assimp中如何判断矩阵是否是单位矩阵
对于一个矩阵元素为浮点型的矩阵,你是否还在使每个元素跟1.0f或0.0f进行比较,如果这样,只能说你的结果不一定正确,那我们看看assimp中是如何做的。
template <typename TReal>
AI_FORCE_INLINE
bool aiMatrix4x4t<TReal…
NO.304 二维区域和检索 - 矩阵不可变
题目
给定一个二维矩阵 matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的 左上角 为 (row1, col1) ,右下角 为 (row2, col2) 。
实现 NumMatrix 类:
NumMatrix(int[][] matrix) 给定整数矩阵 …
短视频矩阵seo系统源码搭建----技术定制化开发
一、需要遵循一下技术开发步骤:
1. 确定需求和功能:明确系统的主要目标和需要实现的功能,包括关键词研究、短视频制作、外链建设、数据分析、账号设置优化等方面。
2. 设计系统架构:根据需求和功能确定系统的架构,包…
线性代数-Python-05:矩阵的逆+LU分解
文章目录 1 矩阵的逆1.1 求解矩阵的逆 2 初等矩阵2.1 初等矩阵和可逆性 3 矩阵的LU分解3.1 LU分解的实现 1 矩阵的逆 1.1 求解矩阵的逆
def inv(A):if A.row_num() ! A.col_num():return Nonen A.row_num()"""矩阵A单位矩阵"""ls LinearSyste…
【考研数学】线性代数第五章 —— 特征值和特征向量(3,矩阵对角化理论)
文章目录 引言三、矩阵对角化理论3.1 一般矩阵的相似对角化3.2 实对称矩阵的相似对角化3.2.1 实对称矩阵相似对角化定理3.2.2 实对称矩阵相似对角化过程 写在最后 引言
承接前文,我们来看看矩阵的对角化理论。
我们前面提到对角化是在矩阵相似那里,若存…
用excel计算一个矩阵的逆矩阵
假设我们的原矩阵是一个3*3的矩阵:
125346789
我们现在要求该矩阵的逆矩阵:
鼠标点到其它空白的地方,用来存放计算结果: 插入-》函数: 选择MINVERSE函数,这个就是求逆矩阵的函数: 点击“继续…
2023注册电气工程师考试大纲
考试大纲如下:
基础考试大纲
一、公共基础
(一)数学
1.1空间解析几何
向量的线性运算;向量的数量积、向量积及混合积;两向量垂直、平行的条件;直线方程;平面方程;平面与平面、直线与直线、平面与直线之间的位置关系;点到平面、直线的距离;球面、母线平行于坐标…
02 MIT线性代数-矩阵消元 Elimination with matrices
一, 消元法 Method of Elimination
消元法是计算机软件求解线形方程组所用的最常见的方法。任何情况下,只要是矩阵A可逆,均可以通过消元法求得Axb的解
eg: 我们将矩阵左上角的1称之为“主元一”(the first pivot),第…
leetcodetop100(18) 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]示例 2: 输入:matrix [[1,2,3…
线性代数笔记:三阶矩阵的特征值计算
三阶矩阵的特征值计算
01 计算理论基础
(1) 行列式方程
设矩阵 A [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] \displaystyle{ {A}\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & …
1.1 向量与线性组合
一、向量的基础知识
两个独立的数字 v 1 v_1 v1 和 v 2 v_2 v2,将它们配对可以产生一个二维向量 v \boldsymbol{v} v: 列向量 v v [ v 1 v 2 ] v 1 v 的第一个分量 v 2 v 的第二个分量 \textbf{列向量}\,\boldsymbol v\kern 10pt\boldsymbol …
【Overload游戏引擎细节分析】视图投影矩阵计算与摄像机
本文只罗列公式,不做具体的推导。 OpenGL本身没有摄像机(Camera)的概念,但我们为了产品上的需求与编程上的方便,一般会抽象一个摄像机组件。摄像机类似于人眼,可以建立一个本地坐标系。相机的位置是坐标原点,摄像机的朝…
Java基础练习(矩阵的加减乘除运算)
简介 对于有了解,但是了解不深的同学,学习Java总是感觉一看就会,一些就废。往往需要一些实操练习,来夯实我们的学习结果。九九乘法表和计算器都是在编程学习领域比较经典的案例。本文为大家讲解一下两个基础实操,熟悉一…
webGL编程指南 第五章 MultiAttributeSize
我会持续更新关于wegl的编程指南中的代码。
当前的代码不会使用书中的缩写,每一步都是会展开写。希望能给后来学习的一些帮助
git代码地址 :git 本章节中我我们学习使用buffer传递数据
<!DOCTYPE html>
<html lang"en"><hea…
2.2 消元法的概念
一、消元法介绍
消元法(elimination)是一个求解线性方程组的系统性方法。下面是使用消元法求解一个 2 2 2\times2 22 线性方程组的例子。消元之前,两个方程都有 x x x 和 y y y,消元后,第一个未知数 x x x 将从第…
线性代数 第四章 线性方程组
一、矩阵形式 经过初等行变换化为阶梯形矩阵。当,有解;当,有非零解。
有解,等价于
可由线性表示
克拉默法则:非齐次线性方程组中,系数行列式,则方程组有唯一解,且唯一解为
其中是…
短视频矩阵营销系统工具如何助力商家企业获客?
1.批量剪辑技术研发
做的数学建模算法,数学阶乘的组合乘组形式,采用两套查重机制,一套针对素材进行查重抽帧素材,一套针对成片进行抽帧素材打分制度查重,自动滤重计入打分。
2.账号矩阵分发开发
多平台,…
微带线的ABCD矩阵的推导、转换与级联-Matlab计算实例
微带线的ABCD矩阵的推导、转换与级联-Matlab计算实例
散射参数矩阵有实际的物理意义,但是其无法级联计算,但是ABCD参数和传输散射矩阵可以级联计算,在此先简单介绍ABCD参数矩阵的基本用法。
1、微带线的ABCD矩阵的推导 其他的一些常用的二端…
VINS-Mono-后端优化 (二:预积分残差雅可比推导)
文章目录 对位置 δ α \delta\alpha δα 进行求导位置误差 δ α \delta\alpha δα 对平移 P b k w P^{w}_{b_{k}} Pbkw 的求导位置 δ α \delta\alpha δα 对旋转 R w b k R^{b_{k}}_{w} Rwbk 进行求导 对速度 δ β \delta\beta δβ 进行求导速度 δ β…
特殊矩阵的压缩存储(对称矩阵,三角矩阵,三对角矩阵,稀疏矩阵)
目录 1.数组的存储结构1.—维数组2.二维数组1.行优先存储2.列优先存储 2.特殊矩阵1.对称矩阵1.行优先存储 2.三角矩阵1.上三角矩阵2.下三角矩阵 3.三对角矩阵(带状矩阵)4.稀疏矩阵 1.数组的存储结构
1.—维数组 各数组元素大小相同,且物理上…
MIT线性代数笔记-第23讲-微分方程,exp(At)
目录 23.微分方程, e x p ( A t ) exp(At) exp(At)用矩阵求解微分方程矩阵指数二阶常微分方程 打赏 23.微分方程, e x p ( A t ) exp(At) exp(At)
用矩阵求解微分方程
例: { d u 1 d t − u 1 2 u 2 d u 2 d t u 1 − 2 u 2 \left \{ \b…
矩阵代数与MATLAB实现(特征值、广义特征值、)
矩阵代数的相关知识 目录
一、特征值与特征向量
1、特征值与特征向量
2、MATLAB计算
二、广义特征值与广义特征向量
1、广义特征值与广义特征向量
2、MATLAB计算
三、酋矩阵
1、酋矩阵
2、MATLAB计算
四、矩阵的奇异值分解
1、奇异值
2、MATLAB计算
五、托普利兹矩…
MIT线性代数笔记-第26讲-复习二
目录 26.对称矩阵及正定性打赏 26.对称矩阵及正定性 实对称矩阵的特征值均为实数,并且一定存在一组两两正交的特征向量 这对于单位矩阵显然成立 证明特征值均为实数: 设一个对称矩阵 A A A,对于 A x ⃗ λ x ⃗ A \vec{x} \lambda…
证明四元数乘法与旋转矩阵乘法等价
刚体四元数姿态控制 一文中没有证明的公式 R ( Q 1 ) R ( Q 2 ) R ( Q 1 ∘ Q 2 ) R(Q_1)R(Q_2)R(Q_1\circ Q_2) R(Q1)R(Q2)R(Q1∘Q2) 在这篇文章中证明。 首先找几个数测试是否等价。 quaternions.py的代码见 自用的四元数、欧拉角、旋转矩阵转换代码。 下面的代码中…
Unity中Shader的矩阵加减法
文章目录 前言一、什么是矩阵矩阵就是一组数的阵列 二、矩阵的加法三、矩阵的负值四、矩阵的减法五、矩阵的表示 前言
Unity中Shader用到的矩阵加减法,以及矩阵的一些基础常识 一、什么是矩阵
矩阵就是一组数的阵列
1 2 3 4 5 6 二、矩阵的加法
两个矩阵相加就是…
Unity中Shader矩阵的逆矩阵
文章目录 前言一、逆矩阵的表示二、逆矩阵的作用四、逆矩阵的计算五、顺序的重要性六、矩阵的逆总结1、求矩阵的逆前,这个矩阵必须得是个方阵2、只有 A x A ^-1^ A^-1^ x A 1时,A的逆才是A^-1^3、求2x2矩阵的逆:交换 a 和 b 的位置…
Unity中Shader矩阵的乘法
文章目录 前言一、矩阵乘以标量二、矩阵和矩阵相乘1、第一个矩阵的列数必须 与 第二个矩阵的行数相等,否则无法相乘!2、相乘的结果矩阵,行数由第一个矩阵的行数决定,列数由第二个矩阵的列数决定! 三、单位矩阵四、矩阵…
简单回顾矩阵的相乘(点乘)230101
[[1 0 1][1 1 0]]
[[3 0 0 3][2 2 1 3][1 3 1 1]]
[[4. 3. 1. 4.][5. 2. 1. 6.]]乘以 c11 a11*b11 a12*b21 a13*b31 1*3 0*2 1*1 4
c12 a11*b12 a12*b22 a13*b32 1*0 0*2 1*3 3
c13a11*b13 a12*b23a13*b33
c14a11*b14 a12*b24a13*b34 c21a21*b11 a22*b21 a23*b…
【总结】坐标变换和过渡矩阵(易忘记)
xCy,此为x到y的坐标变换。 [β1,β2,…,βn] [α1,α2,…αn]C,此为基α到基β的过渡矩阵。 这个概念经常忘记。。。alpha到beta看来就是alpha后面加一个过渡矩阵了,很直观。坐标变换就是根据过渡矩阵和基本形式推一推得到吧,记…
C++实现:实现一个函数,接受一个n x n的矩阵并返回其行列式的值 某知名上市公司笔试题
目录
题目描述:
分析:
实现代码: 题目描述:
实现一个函数,接受一个n x n的矩阵并返回其行列式 如何求解矩阵的行列式? 1x1 矩阵 [[a]] 的行列式为 a。 2x2 矩阵 [ [a, b],[c, d]]的行列式为 a*d - b*c 通过将问题简化为 n 个大小为 n-1 x n-1的矩阵的行列式来计算,可…
线性代数基础【2】矩阵
第二章 矩阵
第一节 矩阵的基本概念与特殊矩阵
一、基本概念
①矩阵
像如下图示的为矩阵,记为A(aij)m*n ②同型矩阵及矩阵相等
若A、B为如下两个矩阵 如果A和B的行数和列数相等,那么A和B为同型矩阵,且A和B的元素相等(即:aijbij),则称A和B相等
③伴随矩阵 设A为mn矩阵(如上…
PCL 已知同名点对计算旋转矩阵并对点云进行旋转
目录 一、 算法概述二、代码实现三、测试示例一、 算法概述 适用:已知三组及三组以上的同名点对,计算旋转矩阵;然后根据旋转矩阵对点云进行旋转,最后保存旋转后的点云文件。 二、代码实现
#include <Eigen/Core>
#include <Eigen/Dense>
线性代数的本质 2 线性组合、张成的空间、基
一种新的看待方式 对于一个向量,比如说,如何看待其中的3和-2? 一开始,我们往往将其看作长度(从向量的首走到尾部,分别在x和y上走的长度)。 在有了数乘后,我们可以将其视为对向量进行…
(done) 如何判断一个矩阵是否可逆?
参考视频:https://www.bilibili.com/video/BV15H4y1y737/?spm_id_from333.337.search-card.all.click&vd_source7a1a0bc74158c6993c7355c5490fc600 这个视频里还暗含了一些引理 1.若 AX XB 且 X 和 A,B 同阶可逆,那么 A 和 B 相似。原因࿱…
核和值域的关系:什么是矩阵的秩?
核和值域的关系:什么是矩阵的秩?
这篇博客将介绍一个任意矩阵的核和值域的关系,并由此说明矩阵秩的意义、子空间维数、子空间正交。
1、矩阵的核:N(A) A ∈ C m n A\in C^{m\times n} A∈Cmn,矩阵的核,记…
【已解决】if lock.acquire(block, timeout):KeyboardInterrupt
问题描述 Traceback (most recent call last): File "/media/visionx/monica/project/ResShift/app.py", line 134, in <module> demo.launch(shareFalse) File "/home/visionx/anaconda3/envs/ResShift/lib/python3.9/site-packages/gradio/bloc…
抖音短视频seo矩阵系统源代码开发系统架构及功能解析
短视频seo源码,短视频seo矩阵系统底层框架上支持了从ai视频混剪,视频批量原创产出,云存储批量视频制作,账号矩阵,视频一键分发,站内实现关键词、短视频批量搜索排名,数据统计分类多功能细节深度…
解线性方程组(一)——克拉默法则求解(C++)
克拉默法则
解线性方程组最基础的方法就是使用克拉默法则,需要注意的是,该方程组必须是线性方程组。 假设有方程组如下: { a 11 x 1 a 12 x 2 ⋯ a 1 n x n b 1 a 21 x 1 a 22 x 2 ⋯ a 2 n x n b 2 ⋯ ⋯ ⋯ a n 1 x 1 a n 2 x 2…
【重点】【矩阵】48.旋转图像
题目
法1:基础好法 class Solution {public void rotate(int[][] matrix) {int n matrix.length;int[][] newMatrix new int[n][];for (int i 0;i < n; i) {newMatrix[i] matrix[i].clone();}for (int i 0; i < n; i) {for (int j 0; j < n; j) {ma…
【数值计算方法(黄明游)】解线性代数方程组的迭代法(一):向量、矩阵范数与谱半径【理论到程序】
文章目录 一、向量、矩阵范数与谱半径1、向量范数a. 定义及性质补充解释范数差 b. 常见的向量范数 l 1 l_1 l1、 l 2 l_2 l2、 l ∞ l_\infty l∞ 范数性质关系 2、矩阵范数a. 矩阵的范数b. 常见的矩阵范数相容范数算子范数 3、谱半径4、知识点总结1. 向量范数2. 矩阵范数…
MIT18.06线性代数 笔记2
文章目录 正交向量与子空间子空间投影投影矩阵和最小二乘正交矩阵和Gram-Schmidt正交化行列式及其性质行列式公式和代数余子式克拉默法则、逆矩阵、体积特征值和特征向量对角化和A的幂微分方程和exp(At)马尔科夫矩阵 傅里叶级数复习二 正交向量与子空间
向量正交:x…
MIT_线性代数笔记:第 16 讲 投影矩阵和最小二乘法
目录 投影 Projections最小二乘法 Least Squares矩阵 A T A^T ATA 投影 Projections
上一讲介绍了投影矩阵 PA( A T A^T ATA) − 1 ^{-1} −1 A T A^T AT,当它作用于向量 b,相当于把 b 投影到矩阵 A 的列空间。 peb,说明 b由两部分组成: p…
【二分查找】【z型搜索】LeetCode240:搜索二维矩阵
LeetCoe240搜索矩阵 作者推荐
【贪心算法】【中位贪心】.执行操作使频率分数最大
本文涉及的基础知识点
二分查找算法合集
题目
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性: 每行的元素从左到右升序排列。 每列的…
方阵的标准型与最小多项式
方阵的标准型与最小多项式 文章目录 方阵的标准型与最小多项式4.1 方阵的特征矩阵【定义】方阵的特征矩阵【定理】方阵与其特征矩阵的关系【定理】可通过初等变换相互转化的矩阵等价的推广【定义】矩阵相似【定理】等价与相似间的充要关系 4.2 方阵的三种因子【定义】方阵的行列…
导行电磁波从纵向场分量求其他方向分量的矩阵表示
导行电磁波从纵向场分量求解其他方向分量的矩阵表示
导行电磁波传播的特点
电磁波在均匀、线性、各向同性的空间中沿着 z z z轴传播,可用分离变量法将时间轴、 z z z轴与 x , y x,y x,y轴分离,电磁波的形式可表示为: E ⃗ E ⃗ ( x , y )…
幺模矩阵-线性规划的整数解特性
百度百科:幺模矩阵 在线性规划问题中,如果A为幺模矩阵,那么该问题具有最优整数解特性。也就是说使用单纯形法进行求解,得到的解即为整数解。无需再特定使用整数规划方法。 m i n c T x s . t . { A x ≥ b x ≥ 0 \begin{align*} min \quad…
【leetcode100-019】【矩阵】螺旋矩阵
【题干】
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 【思路】
不难注意到,每进行一次转向,都有一行/列被输出(并失效);既然已经失效,那我…
短视频矩阵系统的崛起和影响
近年来,短视频矩阵系统已经成为了社交媒体中的一股新势力。这个新兴的社交媒体形式以其独特的魅力和吸引力,迅速吸引了大量的用户。这个系统简单来说就是将海量短视频整合在一个平台上,使用户可以方便地观看和分享好玩有趣的短视频。
短视频…
利用MATLAB构建特殊通用矩阵
在MATLAB编程中,经常需要遇到一些特殊的通用矩阵,本篇主要介绍的是MATLAB中可能会用到特殊矩阵。
1、零矩阵
MATLAB使用zeros函数来创建零矩阵,所谓零矩阵就是矩阵中所有元素皆为0的矩阵。zeros函数的调用方式如下所示:
&#…
线性代数——(期末突击)行列式(上)-行列式计算、行列式的性质
目录
行列式
行列式计算
逆序数
行列式的性质
转置
两行(列)互换
两行(列)对应相等
提公因子
两行(列)对应成比例
某行(列)为零
行列式分裂
行列式变换及三角行列式 行…
线性代数第三课+第四课
矩阵相乘
一行一行相乘
详细过程如图所示
矩阵取绝对值
其实不是科学的说法
其实是取矩阵
就是把括号里面的放到两台竖线之间,然后根据前面的知识来进行计算
常见的结论
如图所示
矩阵的转置
第一行变成第一列,第二行变成第二列
小技巧
先…
opencv003图像裁剪(应用NumPy矩阵的切片)
这一部分相对于马上要学习的二值化是要更更更简单一些的,只需三行,便能在opencv上裁剪图像啦(顺便云吸猫,太可爱了!) 出处见水印!
1、复习图像的显示
前几天期末考试,太久没有看…
D - Swapping Puzzle (交换i和i+1行或者i和i+1列使得a矩阵和b矩阵相同,用next_permutation函数和逆序对)
题目:https://atcoder.jp/contests/abc332/tasks/abc332_d
思想:首先交换行对列中的元素无影响,同理交换列对行的元素无影响。
我们用暴力枚举(两层next_premutation函数)来找到所有的排列方式,同时判断这…
线性代数-第五课,第六课,第七课,第八课
第五课
判断某向量是否可由某向量组线性表示
把向量组组成一个行列式,计算行列式的秩
把所有向量放在一起构成一个行列式,计算行列式的秩
如果两个行列式的秩相等,表示可以线性表示,写答案的格式如下
线性表示:bk…
线性代数_逆矩阵性质
逆矩阵是线性代数中一个非常重要的概念,它具有以下几个基本性质: 1. 可逆矩阵一定是方阵:一个矩阵若要可逆,必须是方阵,即它的行数和列数相等。 2. 逆矩阵的唯一性:如果矩阵\( A \)是可逆的,那么…
线性代数 --- 为什么LU分解中的下三角矩阵L的主对角线上都是1?
为什么LU分解中的下三角矩阵L的主对角线上都是1? 一方面,对于LU分解而言,下三角阵L是对高斯消元过程的记录,是高斯消元的逆过程,是多个消元矩阵E的逆矩阵的乘积(形如下图中的下三角矩阵),即: 另一方面&…
线性代数 --- 为什么LU分解中L矩阵的行列式一定等于正负1?
以下是关于下三角矩阵L的行列式一定等于-1的一些说明 笔者的一些话(写在最前面): 这是一篇小文,是我写的关于求解矩阵行列式的一篇文章中的一部分。之所以把这一段专门提溜出来,是因为这一段相对于原文是可以完全独立的,也是因为我…
正交投影矩阵与透视投影矩阵的推导
正交投影矩阵
正交投影矩阵的视锥体是一个长方体 [ l , r ] [ b , t ] [ f , n ] [l,r][b,t][f,n] [l,r][b,t][f,n],我们要把这个长方体转换到一个正方体 [ − 1 , 1 ] [ − 1 , 1 ] [ − 1 , 1 ] [-1,1][-1,1][-1,1] [−1,1][−1,1][−1,1]中,如下图所…
如何从单应矩阵H中分解旋转矩阵R和平移向量t?
在计算机视觉中,单应矩阵通常用于图像配准和相机标定等任务。下面是使用SVD分解单应矩阵来求解旋转矩阵(R)和平移向量(t)的简要推导过程。
假设求解得到一个单应矩阵H: H [ h 11 h 12 h 13 h 21 h 22 h …
线性代数 --- 矩阵行列式的性质
Determinant det A|A| 矩阵的行列式是一个数,这个数能够反应一些关于矩阵的信息。行列式只对方阵有效。 若矩阵A为: 则A的行列式为: 性质1: 单位矩阵的行列式等于1 性质2:行与行之间的交换会改变det的正负号
以2x2单位…
动手学深度学习4 线性代数
动手学深度学习4 线性代数 1. 线性代数--数学意义2. 线性代数的实现3. 按特定轴求和4. 线性代数QA 1. 线性代数–数学意义
视频:https://www.bilibili.com/video/BV1eK4y1U7Qy/?spm_id_fromautoNext&vd_sourceeb04c9a33e87ceba9c9a2e5f09752ef8 课件ÿ…
线性代数_同济第七版
contents 前言第1章 行列式1.1 二阶与三阶行列式1.1.1 二元线性方程组与二阶行列所式1.1.2 三阶行列式 1.2 全排列和对换1.2.1 排列及其逆序数1.2.2 对换 1.3 n 阶行列式的定义1.4 行列式的性质1.5 行列式按行(列)展开1.5.1 引理1.5.2 定理1.5.3 推论 * …
代码随想录算法训练营第2天 | 977.有序数组的平方 ,209.长度最小的子数组 ,59.螺旋矩阵II
数组理论基础
文章链接:https://programmercarl.com/%E6%95%B0%E7%BB%84%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
977.有序数组的平方
题目链接:https://leetcode.cn/problems/squares-of-a-sorted-array/description/
思路1.暴力排序
将每个数平…
unity urp 视差卡牌
总体效果大概四层,从后往前排序为:卡背、背景、画像、边框
首先卡背比较简单,只要判断如果网格的背面就直接采样卡背图片展示即可
资源准备: 然后是背景,网上找到一张这样的图。 但他还不符合要求,我们的…
抖音矩阵云混剪系统源码多平台多账号一站式管理(免授权版)
抖音矩阵云混剪系统源码 短视频矩阵营销系统V2.2.1(免授权版)
中网智达矩阵营销系统多平台多账号一站式管理,一键发布作品。智能标题,关键词优化,排名查询,混剪生成原创视频,账号分组,意向客户自动采集,智能回复,多账号评论聚合回复,免切换,免登陆发布….助力您在…
科研绘图(六)散点图矩阵
散点图矩阵是一种显示多个变量之间关系的数据可视化工具,特别是当数据集包含三个或多个变量时,这种图表非常有用。这种图通常在探索性数据分析中使用,以便快速理解数据集中变量之间的关系。在散点图矩阵中,每行和每列都代表数据集…
【深度学习笔记】02 线性代数基础
线性代数基础 线性代数基础标量向量长度、维度和形状矩阵张量算法的基本性质降维非降维求和点积(Dot Product)矩阵-向量积矩阵-矩阵乘法范数 线性代数基础
标量
标量由只有一个元素的张量表示
import torchx torch.tensor(3.0)
y torch.tensor(2.0)…
矩阵滑动窗口|36. 有效的数独 3. 无重复字符的最长子串
题目:请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例…
搜索经典题——填充 9*9矩阵
题目:给定一个九行九列矩阵,填充矩阵元素,要求: 1、每一行每一列,每个小九宫格(图片画粗的地方就是)不能包含相同元素 2、每一行,每一列,每个小九宫格均会完整出现1-9的数…
线性代数的学习和整理23:用EXCEL,VBA,python计算向量/矩阵的各种乘法:内积,点积,外积,叉积(建设ing)
目录
前言:EXCEL里的的向量相关计算公式
0.1 EXCEL里相关公式
0.2 先说结论:向量组的点乘公式和 向量组的点乘公式不一样
1 向量的点乘 (内积)
1.1 向量的点乘公式
1.2 EXCEL里向量点乘的计算
编辑
1.3 向量点乘的性质
1.3.1 内积的公式…
线性代数:逆、转置、分块、多项式 矩阵公式总结
目录
逆矩阵、转置矩阵重要公式
公式 证明
矩阵分块
基本运算
分块的逆(主副对角线分块对角阵的逆、主副对角线上下三角分块对角阵的逆)
例
矩阵多项式
例
克拉默法则及逆矩阵求方程组 逆矩阵、转置矩阵重要公式
公式 证明 矩阵分块
基本运…
【线性代数与矩阵论】范数理论
范数理论
2023年11月16日 文章目录 范数理论1. 向量的范数2. 常用向量范数3. 向量范数的等价性4. 矩阵的范数5. 常用的矩阵范数6. 矩阵范数与向量范数的相容性7. 矩阵范数诱导的向量范数8. 由向量范数诱导的矩阵范数9. 矩阵范数的酉不变性10. 矩阵范数的等价性11. 长方阵的范数…
【易混区分】 tensor张量 Numpy张量的各种矩阵乘法、点积的函数对比 (dot, multiply,*,@matmul)
文章目录 1 矩阵运算基本概念1.1 点积1.2 矩阵乘法 2 dot()3 multiply() 和 *4 matmul和 1 矩阵运算基本概念
1.1 点积
又称为数量积、标量积(scalar product)或者内积(inner product)
它是指实数域中的…
线性代数基础【6】二次型
第一节、二次型的基本概念及其标准型
一、基本概念
①二次型
含n个变量x1,x2,…,xn,且每项都是2次的齐次多项式
②标准二次型
只含有平方项不含交叉项的二次型称为标准二次型
③二次型的标准化
设f(X)X^TAX 为一个二次型,经过可逆的线性变换XPY(即P为可逆矩阵)把二次型…
Pytorch-统计学方法、分布函数、随机抽样、线性代数运算、矩阵分解
Tensor中统计学相关的函数
torch.mean() #返回平均值
torch.sum() #返回总和
torch.prod() #计算所有元素的积
torch.max() # 返回最大值
torch.min() # 返回最小值
torch.argmax() #返回最大值排序的索引值
torch.argmin() #返回最小值排序的索引值
torch.std() #返回标准差
…
C语言:矩阵中的最小元素
题目描述
给定一个5X5的整数矩阵,找出其中最小的元素,输出所在的行号、列号和元素值,其中行号和列号都从0开始。 例如,有矩阵: 5 86 53 50 18 25 67 79 44 68 79 63 24 84 100 42 30 59 47 37 28 10 32 23 81 其中最小…
线性矩阵不等式LMI与李雅普诺夫Lyapunov稳定性
文章目录 线性矩阵不等式(Linear Matrix Inequality,LMI)例子 Lyapunov稳定性Schur Complement定义Schur Complement作用/性质利用Schur Complement将LMI和Lyapunov联系起来 线性矩阵不等式(Linear Matrix Inequality,…
推荐系统|召回05_矩阵补充、最近邻查找
文章目录 矩阵补充Matrix Completion模型结构模型训练模型存储 矩阵补充Matrix Completion
模型结构 通过用户ID和物品ID分别找到对应的向量,然后去做内积,内积的数值可以去衡量匹配的程度。 不共享参数的意思是指用户ID和物品ID使用不同的Embedding L…
【数字信号处理】FFT
FFT
2023年11月18日 #elecEngeneer
【数字信号处理】DFT 文章目录 FFT1. 快速傅里叶变换-FFT1.1 时间抽取FFT(Decimation-in-time algorithm)1.2 FFT做多项式乘法(卷积)1.2.1 多项式乘法与卷积1.2.2 多项式与DFT1.2.3 多项式乘法…
【算法题】73. 矩阵置零
题目
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]] 示例 2: 输…
python数学建模--线性规划问题案例及求解
目录数学问题:线性规划问题程序设计结果分析实际应用1:加工厂的生产计划设置未知数建立数学模型程序设计结果分析实际应用2:油料加工厂的采购和加工计划设置未知数建立数学模型程序设计结果分析遗留的问题钢管加工用料问题分析scipy.optimize…
3.4 齐次方程组基础解系
基本解法 在线性空间求基的时候,经常会遇到齐次方程组基础解系的问题,比如以下齐次线性方程组: (321000000)v(000)\begin{pmatrix}3&2&1\\0&0&0 \\0&0& 0\end{pmatrix}v \begin{pmatrix}0\\0\\0\end{pmatrix} ⎝⎛…
奇异值分解(SVD)原理与在降维中的应用
奇异值分解(SVD)原理与在降维中的应用 奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算…
乘法逆元之欧几里得和扩展欧几里得
乘法逆元 文章目录乘法逆元一、模运算的性质二、除法的模运算1、除法模运算2、解决除法模运算问题三、乘法逆元1、定义2、**逆元是干什么的呢**四、求解逆元1、费马小定理2、扩展欧几里得(exgcd)(1)裴蜀定理(2…
奇异值分解在图形压缩中的应用
奇异值分解在图形压缩中的应用 在研究奇异值分解的工程应用之前,我们得明白什么是奇异值?什么是奇异向量? 奇异值与奇异向量
概念:奇异值描述了矩阵在一组特定向量上的行为,奇异向量描述了其最大的作用方向。
奇异值…
林浩然矩阵江湖历险记
林浩然矩阵江湖历险记 Lin Haoran’s Matrix Adventures 在那充满神秘色彩的矩阵世界里,林浩然面对的挑战是驯服一个具有六个个性元素的23矩阵——“小三儿”。这个矩阵由两行三列组成,每一个元素都像是棋盘上的一枚棋子,它们紧密排列在一起&…
00. 线性代数的本质
写在前面
此分类为b站视频《线性代数的本质》系列的个人笔记,也可以供大家参考。视频很通俗,但是需要高中以上水平,最好学过大学线性代数,以便用一个“新的”角度看待线代,当然也适合考研党看一看。笔记里包含了视频截…
03 - 矩阵与线性变换
回到目录
03 - 矩阵与线性变换 线性“变换”就像“函数”的概念,即,“向量的函数”,只是它可以操纵空间。 线性变换和其他的非线性变换的区别?(操纵空间的原则) 网格线之间保持平行和等距原点不变 因此什…
前缀和【一维前缀和与二维前缀和】
全文目录😀 一维前缀和🤔 构建一维前缀和数组😵💫 子序列的和😀 二维前缀和🤔 构建二维前缀和数组😵💫 子矩阵的和😀 一维前缀和
一维前缀和很简单,就是…
【操作系统原理实验】银行家算法模拟实现
选择一种高级语言如C/C等,编写一个银行家算法的模拟实现程序。1) 设计相关数据结构;2) 实现系统资源状态查看、资源请求的输入等模块;3) 实现资源的预分配及确认或回滚程序;4) 实现系统状态安全检查程序;5) 组装各模块…
歌德巴赫猜想数学证明
歌德巴赫猜想数学证明证明方法一: 歌德巴赫猜想的证明需要借助数学理论,其中包括数论和组合数学等方面的知识。以下是一种基于矩阵和组合数学的证明方法:首先,定义一个n*n的01矩阵A,其中A[i][j]表示第i个偶数是否可以表示为第j个质…
混淆矩阵Confusion Matrix(resnet34 基于 CIFAR10)
目录
1. Confusion Matrix
2. 其他的性能指标
3. example
4. 代码实现混淆矩阵
5. 测试,计算混淆矩阵
6. show
7. 代码 1. Confusion Matrix
混淆矩阵可以将真实标签和预测标签的结果以矩阵的形式表示出来,相比于之前计算的正确率acc更加的直观…
Sub-Gaussian随机变量
文章目录引言Sub-Gaussian等价的几个性质Sub-Gaussian随机变量的定义Sub-Gaussian随机变量的三个例子Sub-Gaussian的近似旋转不变性总结引言
Sub-Gaussian的分布跟标准高斯分布N(0,1)\mathcal N (0,1)N(0,1)的性质密切相关,因此在介绍Sub-Gaussian随机变量之前&…
[Eigen中文文档] 从入门开始...
文档总目录 本文目录如何安装Eigen第一个简单的程序编译和运行第一个程序第一个程序的解释示例2:矩阵和向量解释第二个例子本文英文原文链接
这是一个非常简短的Eigen入门文章。该文章有两层目的。对于想要尽快开始编码的人来说,该文章是对Eigen库的最简…
MATLAB简单图形绘制(五)
实验目的 1)掌握MATLAB图形绘制的基本原理和方法; 2)熟悉和了解MATLAB图形绘制程序编辑的基本指令; 3)掌握利用MATLAB图形编辑窗口编辑和修改图形界面,并添加图形的各种标注; 4)掌握…
3.6.3数据库系统-模式分解:是否保持函数依赖、保持函数依赖分解定义、无损分解、表格法、公式法
3.6.3数据库系统-模式分解:是否保持函数依赖、保持函数依赖分解定义、无损分解、表格法、公式法是否保持函数依赖保持函数依赖分解定义例题无损分解表格法例题公式法例题是否保持函数依赖
函数依赖是通过某一个维度可以函数决定另一个部分,这里在关系模…
数学建模第一天:数学建模先导课之MATLAB的入门
目录
一、MATLAB的简介
二、Matlab基础知识
1. 变量
①命名规则
②特殊变量名
2、数学符号与函数调用
①符号
②数学函数
③自定义函数
三、数组与矩阵
1、数组
①创建数组
②访问数组元素
③数组运算
2、矩阵
①定义
②特殊矩阵
③矩阵运算
四、控制流
…
【射影几何08】仿射映射
一、说明 简单来说,“仿射变换”就是:“线性变换”“平移”,但这是在笛卡尔坐标下的表现,然而在射影几何中,其中有更合乎逻辑的解释。本文讲仿射映射的定义,以及仿射不变性的特点。
二、仿射映射
2.1 直线…
主成分分析(PCA)直观理解与数学推导
近期在完成信息论的作业,发现网上的资料大多是直观解释,对其中的数学原理介绍甚少,并且只介绍了向量降维,而没有介绍向量重构的问题(重构指的是:根据降维后的低维向量来恢复原始向量)࿰…
C语言刷题系列——8.矩阵的行/列互换
🚩矩阵的行/列互换⛄一) 题目要求⛄二) 题解step1:输入矩阵step2:输入k(执行 行/列 互换操作的次数)step3:(循环内部)行/列互换step4:打印互换后的矩阵⛄三) 最终的实现⛄一) 题目要求
输入描述:第一行包含两个整数n和mÿ…
[Eigen中文文档] 稀疏矩阵操作
文档总目录 本文目录 稀疏矩阵格式SparseMatrix 类 第一个示例SparseMatrix 类矩阵和向量属性迭代非零系数 填充稀疏矩阵支持的运算符和函数基本操作矩阵乘积块操作三角形视图和自共轭视图 英文原文(Sparse matrix manipulations)
处理和解决稀疏问题涉及各种模块,…
兩獨立隨機變數之和的特徵函數
兩獨立隨機變數之和的特徵函數參考機率論 特性函數(1) - Properties,特徵函數(characteristic function)的定義為:φX(t)E(eit(X))\varphi_{X}(t)\operatorname{E}\left(e^{it(X)}\right)φX(t)E(eit(X))。 φXY(t)E(eit(XY))套用特徵函數的定義E…
兩矩陣乘積的跡對矩陣微分公式證明
兩矩陣乘積的跡對矩陣微分公式證明前言證明前言
本公式來自The Matrix Cookbook中的公式(104)。 證明 ∂tr(AXT)∂X∂∑i,jAijXij∂Xtr(ABT)∑i,jAijBij[∂∑i,jAijXij∂X11...∂∑i,jAijXij∂X1n...∂∑i,jAijXij∂Xm1...∂∑i,jAijXij∂Xmn][A11...A1n...Am1...Amn]A\begin{…
高斯消元法解线性方程组和矩阵求逆(C++面向对象实现)
实现了两个向量和矩阵的基本类,针对处理对象创建了MatrixVector类和MatrixMatrix类。使用gauss法同时实现了线性方程组的求解和矩阵的求逆 文章目录0. 预处理1. Vector向量类2. Matrix矩阵类3. MatrixVector类4. MatrixMatrix类5. 运行调用0. 预处理
#include <…
【算法题】神奇的斐波那契数列(Fibonacci sequence)、青蛙跳台阶问题、矩阵中的路径
神奇的斐波那契数列和青蛙跳台阶问题 一、神奇的斐波那契数列1.1、题目描述1.2、递归算法1.3、迭代法1.4、小结 二、青蛙跳台阶问题2.1、题目描述2.2、思路2.3、动态规划法2.4、小结 三、矩阵中的路径3.1、题目描述3.2、思路3.3、代码实现3.4、小结 总结 一、神奇的斐波那契数列…
旋转机械设备故障诊断的轴心轨迹总结
旋转机械设备故障诊断的轴心轨迹分析 1. 转子不对中故障2. 转子不平衡2.1 文献1轨迹2.2 文献2轨迹4. 轴弯曲故障5. 转子部件松动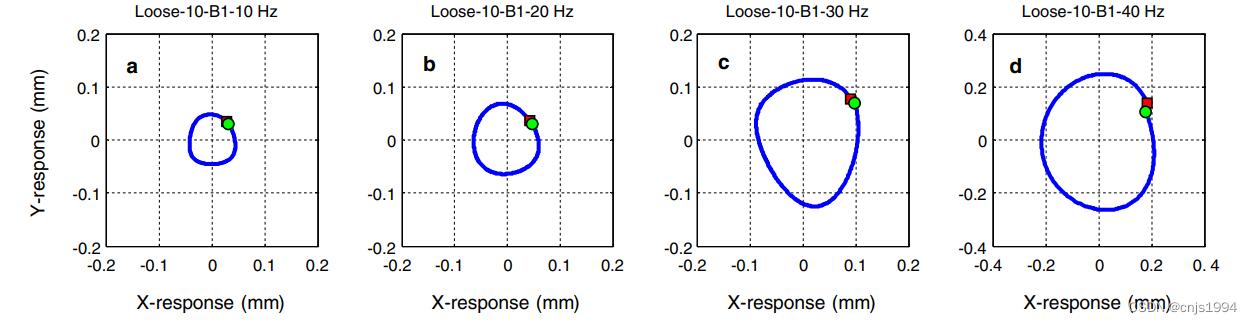6. 碰摩故障3. 典型转子故障的原因1. 转子不对中故障 …
短视频seo矩阵系统源码开发思路
短视频SEO矩阵系统源码开发,需要遵循一下步骤:
1. 确定需求和功能:明确系统的主要目标和需要实现的功能,包括关键词研究、短视频制作、外链建设、数据分析、账号设置优化等方面。
2. 设计系统架构:根据需求和功能确定…
Matlab中exp(x)函数的用法
目录1.语法2.说明3.示例e的数字表示形式欧拉恒等式为指数函数绘图4.参考来源:1.语法
Yexp(X)2.说明
Yexp(X)为数组X中的每个元素返回指数exe^xex。对于复数元素zxiy,它返回以下复指数ezex(cosyisiny)e^{z}e^x(cosyisiny)ezex(cosyisiny)。 使用expm计算…
华为OD机试题,用 Java 解【和最大子矩阵】问题 | 含解题说明
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典本篇题目:和最大子矩阵
题目
给定一个二…
MATLAB学习笔记2:MATLAB基础知识(中)
阅读前请注意:
1. 该学习笔记是华中师范大学HelloWorld程序设计协会2021年寒假MATLAB培训的学习记录,是基于培训课堂内容的总结归纳、拓展阅读。博客内容由 K2SO4钾 撰写、编辑,发布于 K2SO4钾 的个人投稿与华中师范大学HelloWorld程序设计协…
刚体运动以及坐标变换-1
文章目录刚体运动和坐标变换-1基础代数欧式变换四元数用四元数表示旋转刚体运动和坐标变换-1
基础代数
外积: a\bf aa 和 b\bf bb 两个向量的外积代表一个垂直这两个向量的向量,大小为 ∣a∣∣b∣sin⟨a,b⟩\bf |a||b|\sin\langle a, b\rangle∣a∣∣…
C#,码海拾贝(02)——复数Complex计算类,《C#数值计算算法编程》源代码升级改进版
一、周长发《C#数值计算算法编程》1.1图书简介 《C#数值计算算法编程》是2007年1月1日电子工业出版社出版的图书,由周长发编写。ISBN:9787121032035本书囊括了近90个实用经典算法,每一个算法都独立成节。每一节都包括算法原理、算法实现和示例3个部分。算…
ThreeJS-太阳球围绕旋转(二十四)
数学小知识:
我们根据旋转角度θ可以计算出任意时刻的x,y
sinθ y0/r; 因此y0 rsinθ,
cosθ x0/r,因此x0 rcosθ,
小拓展: y0^ x0^ - r^2*sinθ^2 r^2*cosθ^2 r^2*(sinθ^2 cosθ^2) r^2;
这也是为什么在极坐标方程中
y0 rsinθ,
x0 rcos…
计算方法 4.线性方程组解法(2)
记得上一期的高斯消元吗,现在把它写成矩阵相乘的形式: 通过不断的左乘Ln矩阵就可以起到这样的效果,每乘一个就可以消掉一行,总共要n-1次。 这里思考一个问题:L的逆矩阵是怎么样的?: 这样我们就可…
C#,码海拾贝(13)——矩阵及其基本计算类Matrix的源代码,《C#数值计算算法编程》源代码升级改进版
1、矩阵及其历史 1.1 矩阵
矩阵,数学术语。在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。 矩阵是高等代数学中…
C#,码海拾贝(18)——矩阵的(一般)三角分解法(Triangular Decomposition)之C#源代码,《C#数值计算算法编程》源代码升级改进版
1 三角分解法 Triangular Decomposition
三角分解法亦称因子分解法,由消元法演变而来的解线性方程组的一类方法。设方程组的矩阵形式为Axb,三角分解法就是将系数矩阵A分解为一个下三角矩阵L和一个上三角矩阵U之积:ALU,然后依次解…
第一性原理计算在材料分析中的应用及未来发展趋势
第一性原理计算是一种理论计算方法,能够基于量子力学原理对物质的性质进行高精度预测。它已经成为材料科学研究中不可或缺的工具,帮助我们了解材料的基本特性,优化材料的性能,并发现新的材料。 一、第一性原理计算的基本原理
第一…
稀疏矩阵存储格式总结
稀疏矩阵是指矩阵中的元素大部分是0的矩阵,实际问题中大规模矩阵基本上都是稀疏矩阵,很多稀疏度在90%甚至99%以上,大规模的稀疏造成了大量无效数据的计算和存储资源占用,也无法有效的载入有限内存计算。因此我们需要有高效的稀疏矩阵存储格式…
武忠祥老师每日一题||定积分基础训练(九)
∫ 0 1 ln ( 1 x ) ( 2 − x ) 2 d x \int_{0}^{1}\frac{\ln (1x)}{(2-x)^2}\,{\rm d}x ∫01(2−x)2ln(1x)dx 根据题目的特点,有对数函数、有理函数,两种不同类型的函数相乘,对此,应用分部积分法。 当出现对数后ÿ…
【高数+复变函数】傅里叶级数
文章目录 1. 傅里叶级数1.1 和差化积积化和差1.2 三角函数系的正交性1.3 系数公式求解1.4 展开条件1.5 变形下的傅里叶 在课程学习中,感觉这一部分的东西频繁会被用到,因此写下来做个总结。 1. 傅里叶级数
在科学技术中,常常会遇到各种各样的…
满秩方阵的特征值分解与它的奇异值分解,这两个结果一样吗?
满秩方阵的特征值分解和奇异值分解是不同的两个分解过程。
对于一个 n n n \times n nn 的实对称矩阵,它的特征值分解为 A Q Λ Q − 1 AQ\Lambda Q^{-1} AQΛQ−1,其中 Q Q Q 是正交矩阵, Λ \Lambda Λ 是对角矩阵,对角线…
14.1 矩阵幂级数
文章目录 矩阵的幂矩阵幂的极限谱半径与范数矩阵幂级数 矩阵的幂 现在讨论下矩阵的n次方的问题,比如下面的矩阵: A 1 ( 2 1 − 1 1 2 − 1 − 1 − 1 2 ) A 2 ( 6 5 − 5 5 6 − 5 − 5 − 5 6 ) A 3 ( 22 21 − 21 21 22 − 21 − 21 − 21 22 ) A^…
线性代数 --- Gram-Schmidt, 格拉姆-施密特正交化(下)
Gram-Schmidt正交化过程 到目前为止,我们都是在反复强调“对于无解的方程组Axb而言,如果矩阵A是标准正交矩阵的话,就怎么怎么好了。。。。”。因为,不论是求投影还是计算最小二乘的正规方程,他们都包含了。当A为标准正…
最优化理论-线性规划中的大M法的步骤
目录:
一、引言 二、线性规划的基本概念 三、最优化理论中的大M法 1. 大M法的基本思想 2. 大M法的步骤 3. 大M法的优缺点 四、大M法的应用 1. 生产计划问题 2. 运输问题 3. 投资问题 五、总结
一、引言
最优化理论是数学中的一个重要分支…
机器学习-线性代数-逆映射与向量空间
逆映射与向量空间
一、逆映射
矩阵的本质是映射。对于一个 m n m n mn的矩阵,乘法 y A x y Ax yAx的作用就是将向量从 n n n维原空间中的 x x x坐标位置,映射到 m m m维目标空间的 y y y坐标位置,这是正向映射的过程。那么,…
Eigen中用于特征值分解的几个类的介绍
本文参考于 https://eigen.tuxfamily.org/dox/group__TopicLinearAlgebraDecompositions.html
很多场合我们需要去计算矩阵的特征值与特征向量,但是Eigen中有好几个计算特征值与特征向量的方法,这些方法到底该选哪个呢?这篇文章就带着大家来…
短视频矩阵是什么?源码搭建技术干货
一、短视频账号矩阵是什么?
短视频账户矩阵实际上是通过一些技术手段将账户和账户连接起来的。这种账户有一定的相关性。通过相互吸引流量,可以扩大账户的影响力,使账户拥有更多的粉丝和更高的价值。短视频账户矩阵属于短视频营销策划的高级…
SLAM十四讲——ch4实践(李群李代数)
视觉SLAM14讲----ch4的操作及避坑 一、ch4的实践的准备工作二、各个实践操作1. Sophus的基本使用方法2. 例子:评估轨迹误差 三、遇到的问题 一、ch4的实践的准备工作
确保已经有Sophus库,Sophus库是一个较好的李代数库。
注意: 开始时slamb…
C语言用高斯消元法求行列式
目录
数学原理
程序设计
整体流程与代码
测试函数
测试结果 数学原理
高斯消元法求行列式:利用初等行变换,化为上三角行列式,求其主对角线的乘积
行列式的初等行变换:
1)换行变换:交换两行…
《机器学习线性代数基础:Python语言描述》读书笔记----向量
什么是向量
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。
直观地说,把一组数字排列成一行或一列,就成为向量。
如[4,5],可…
pytorch——张量的数学运算
这里的乘法表示element-wise矩阵中对应位置元素相乘
atorch.randn(3,4)
btorch.randn(4)
print(a)
print(b)
print(ab)
print(torch.add(a,b))
print(a-b)
print(torch.sub(a,b))
print(a*b)
print(torch.mul(a,b))
print(a/b)
print(torch.div(a,b))matmul表示矩阵乘法&#…
爆款视频生成器小程序源码搭建方案
爆款视频生成器是一种可以帮助用户快速制作出高质量视频的工具。它可以根据用户提供的素材、模板和音乐等要素,自动生成一个精美的视频。这种工具可以大大节省用户的时间和精力,同时还能够提高视频制作的效率和质量,使视频更易于被观众接受和…
《程序设计基础》 第七章 数组 7-16 找鞍点 (20 分)
一个矩阵元素的“鞍点”是指该位置上的元素值在该行上最大、在该列上最小。
本题要求编写程序,求一个给定的n阶方阵的鞍点。
输入格式:
输入第一行给出一个正整数n(1≤n≤6)。随后n行,每行给出n个整数,其…
《程序设计基础》 第五章 函数 例题5-2 使用函数计算五边形的面积 (10 分)
本题要求实现2个函数,分别判断3条边能否构成一个三角形和计算三角形的面积,使得可以完成五边形面积的计算。题目保证计算结果不超过双精度范围。 将一个五边形分割成3个三角形(如上图所示),输入这些三角形的7条边长&am…
概率密度函数及其在信号方面的简单理解(中)频谱密度函数
概率密度函数及其在信号方面的简单理解(中)频谱密度函数
(中)频谱密度函数傅里叶级数傅里叶变换参考文献后记 上学期修了外学院的自动控制原理课,学习非线性控制系统的处理时用到了傅里叶级数,老师就让我…
计算机组成原理 :处理器设计
单核计算机系统: cpu的组成: 如何设计一个处理器?:
支持简单指令集的处理器实例: 回顾一下格式: 因此我们可以看出我们的需求: 数据通路组件选择: 我们使用的组件有哪些?…
VAMP由浅入深(Part-3:状态演进分析数学基础(续))
文章目录考虑一般的收敛结论对定理4的证明证明方法对初始条件的确认数学归纳的推导这部分的小结考虑一般的收敛结论
对任意维度 NNN,给定一个正交阵V∈RNN\boldsymbol V \in \mathbb R^{N \times N}V∈RNN,以及一个初始向量u0∈RN\boldsymbol u_0 \in \…
计算方法 2.非线性方程和方程组的数值解法
主要是学习各种近似解法。 求根步骤: 二分法: 迭代法: 就是把f(x)0变幻成了xu(x),我解出后面那个方程也就是解出了f(x)0.而后面那个很经典,就是不懂点嘛。 P阶收敛就是wi1wi^p*C(这个c就是歌姬吧,主要是p&a…
一阶常系数微分方程组的笔记
文章目录一、一阶线性常系数齐次微分方程组1.1 基本定义1.2 解的存在性1.3 解的唯一性1.4 结论二、一阶线性常系数非齐次微分方程组2.1 基本定义2.2 解的存在性三、例题一、一阶线性常系数齐次微分方程组
1.1 基本定义 {dx1(t)dta11x1(t)a12x2(t)⋯a1nxn(t)dx2(t)dta21x1(t)a2…
近世代数:正规子群的同态与同构
我们要更加深入地学习同态与同构。先来学习一下那些符号: 这里要强调一下概念:同态映射不一定是满射,因此有同台映射的两个群不一定是同态,必须是要有满射的。自同态与自同构主要体现的是那个映射比较特别,毕竟群肯定和…
[Eigen中文文档] 概述(总目录)
一、概述
英文原文链接
这是 Eigen3 的API文档,你可以下载它以便于离线阅读。
以下是该中文文档目录,分为四部分: 入门
对于第一次接触Eigen,学习Eigen最好的方法就是阅读该文档,这可以让你学会如何使用Eigen编写…
单视图测量 (2D变换、影消点线、单视图重构)
写在前面:本篇Blog仅作为学习笔记,学习内容来自于北邮CV-XUEBA团队的三维重建(精简版,鲁鹏)课程。
回顾经典2D变换 等距变换 旋转矩阵(Rotate Matrix)的性质分析
证明:旋转矩阵是正交矩阵
相似变换 仿射变换 因为6个自由度&am…
矩阵向量乘法MPI程序的性能评估
文章目录 前言一、实验代码二、实验运行效果三、问题以及思考总结 前言
要求:对矩阵向量乘法MPI程序进行不同输入规模、不同进程数的执行和计时,并对得到运行时间进行计算分析,据此评价该程序的强扩展性和弱扩展性。最后总结学习心得&#x…
近世代数:置换群、陪集指数和Lagrange定理
置换群,顾名思义,就是置换组成的群,这个置换就是双射变换的意思,因此大家都是对称群的子群。大家老换来换去的也不分谁是谁了,干脆就1234表示吧。K-循环就是大家像跑火车一样跑一圈。 无公共数码的意思是两个轮换&…
[现代控制理论]2_state-space状态空间方程
[现代控制理论]11_现代控制理论串讲_完结_pdf获取 [现代控制理论]10_可观测性与分离原理_观测器与控制器 [现代控制理论]9_状态观测器设计_龙伯格观测器 [现代控制理论]8.5_线性控制器设计_轨迹跟踪simulink [现代控制理论]8_LQR控制器_simulink [现代控制理论]7_线性控制器设计…
OpenGL入门第四次实验 几何变换(一)
链接: https://pan.baidu.com/s/1cBTTbbzRCVBCX_H4jf6qMA 提取码: kj8w 一、实验原理 本次实验利用OpenGL的GLFW库以及glm进行几何变换操作,实现了作业的两个要求。 GLFW是一个用于OpenGL应用程序开发的可移植库。它处理与OpenGL上下文创建、窗口管理、分辨率切换、…
OpenGL入门第二次实验 直线光栅化算法
代码都放在一起了,如果接下来的实验有需要私信一下就好哦 链接: https://pan.baidu.com/s/1cBTTbbzRCVBCX_H4jf6qMA 提取码: kj8w 第二次实验作业 直线光栅化算法 实验报告
老师的评语是:实验正确实现了任意斜率情况下的画直线算法,且可以通…
304. 二维区域和检索 - 矩阵不可变——动态规划
一维前缀和
class NumMatrix {
public:vector<vector<int>> dp;NumMatrix(vector<vector<int>>& matrix) {//一开始思考,不是每次直接加起来就好了吗//后来发现,这样消耗的时间也太多了吧,怪不得我AC不了//看了…
python 二维相关系数计算
在matlab中要计算两个矩阵的相关系数只需调用corr2()即可,但 python中好像没有对等的函数(主要是我没找到),因此根据公式实现,并与matlab的结果对比,发现结果一致。
公式matlab文档…
《机器学习线性代数基础:Python语言描述》读书笔记----对角矩阵
对角矩阵
使用对角矩阵来描述某一个向量的空间变换有如下优点: 一个n维列向量在n阶对角矩阵矩阵的作用下,其线性变换的方式仅仅反映在个个维度轴向上的长度拉伸,而不对应着平移或旋转变换,即Ax[a1a2a3⋱an][x1x2x3⋮xn][a1x1a2x2…
使用omp并行技术实现矩阵乘法
矩阵乘法: OpenMP基本概念 OpenMP是一种用于共享内存并行系统的多线程程序设计方案,支持的编程语言包括C、C和Fortran。OpenMP提供了对并行算法的高层抽象描述,特别适合在多核CPU机器上的并行程序设计。编译器根据程序中添加的pragma指令&…
【Matlab优化求解】遗传算法求解车辆发车间隔优化问题【含源码 132期】
一、代码运行视频(哔哩哔哩)
【Matlab优化求解】遗传算法求解车辆发车间隔优化问题【含源码 132期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]裴玉龙,杨世军,潘恒彦.考虑车内拥挤状态的公交弹性发车间隔优化[J]. 东北大学学报(自…
线性规划技巧: 如何写对偶问题
给定一个优化问题,我们去理解它的时候,或者设计算法的时候,可以研究它的对偶。
有时候原问题不好解,但它的对偶相对容易。这个时候,可以从对偶问题出发,进而寻求原问题的解。
这篇文章总结了线性规划的对…
LIF神经元膜电压公式-迭代式推导,及其在STBP中的应用
膜电压公式 τmdudt−[u−urest]RI(t)\tau _m\frac{du}{dt}-[u-u_{rest}]RI(t) τmdtdu−[u−urest]RI(t)
迭代式1 u(tΔt)u(t)e−ΔtτmRI(t)u(t\Delta t)u(t)e^{-\frac{\Delta t}{\tau m} }RI(t)u(tΔt)u(t)e−τmΔtRI(t)
推导
当tt0tt_0tt0时,u(t)…
动态图理解向量的含义
向量的含义1. 从物理学的角度,向量是 空间中的箭头 ,决定一个向量的是它的长度(Length)和它所指的方向(Direction),只要这两个特征相同,可以自由移动一个变量而使它保持不变。平面中…
LOJ #2269. 「SDOI2017」切树游戏 题解
LOJ #2269. 「SDOI2017」切树游戏#2269. 「SDOI2017」切树游戏 没错我在某谷被卡掉了,之后会了全局平衡二叉树再更新那个做法。 不考虑修改怎么做。
设 f(i,j)f(i, j)f(i,j) 表示以 iii 为根的子树(必须包含点 iii)异或值为 jjj 的方案数&am…
全国大学生数学竞赛备考——高数上(极限、导数、微分、积分、级数)
我真的会忘(3)极限两个重要极限公式常用极限公式导数、微分与积分牛顿-莱布尼茨公式莱布尼兹公式微分中值定理罗马中值定理拉格朗日中值定理柯西定理泰勒公式几个常见的麦克劳林公式洛必达曲率曲率圆牛顿迭代法积分中值定理分部积分法级数正项级数审敛法…
数字图像处理MATLAB学习笔记(四)
数字图像处理MATLAB学习笔记(四)
Geometric Transformations and Image Processing
1 Transforming Points
点变换就是进行空间坐标系统的转换,即将一个在空间a的点映射到空间b中去。
我们可以将这种输入到输出的正向的空间映射用公式表达…
POJ 3613 Cow Relays 题解
POJ 3613 Cow RelaysPOJ 3613 Cow Relays 真心想吐槽一下,这个不能用 111111 真的挺难受的。 首先看去像一个板子题,之后发现如果直接对于每个点建图的话时间是过不了的。
之后发现边的数量其实不是很多,一条边最多只有两个不同的点…
poj3146 题解
poj3146
题目大意:
给定一个 n,pn, pn,p 求 (n0…n)\binom{n}{0 \dots n}(0…nn) 有多少数不能被 ppp 整除。
我们考虑 LucasLucasLucas 定理。 (nm)(n/pm/p)(nmodpmmodp)\binom{n}{m} \binom{n / p}{m/ p} \times \binom{n \mod p}{m \mod p}(mn)(m/pn/p…
微分几何在机器人领域的应用
微分几何基础
微分几何是现代数学领域中的重要分支,在理论探索和实际应用中都是重要学科。大名鼎鼎的高斯、欧拉是微分几何学派的创建者(是否记得多少公式和定理以这两人的名字命名)。20世纪是微分几何发展迅猛的100年,中国的数学…
R语言 复习笔记(4)High Dimentional Visualization and Analysis
week 4 1 Movie rating data 1.1 Data precossing 1.2 Data input and IDA 1.3 Hierarchical clustering
hclust(): Hierarchical 聚类,method分3种:complete,single,average cutree(): 将tree型结构进…
2023年计算机考研英语一作文模板|考研要不要使用英语模板?
2023年计算机考研英语考英语一,计算机考研基本是考计算机科学与技术这个大类,属于学硕,考研英语一是全国统一的。那么2023年计算机考研英语一作文怎么写呢?要不要参考模板呢?
首先请看下2023年计算机考研英语一作文模板:建议信…
线性代数Python计算:线性方程组的最小二乘解
给定ℝ上无解线性方程组Axb\boldsymbol{Ax}\boldsymbol{b}Axb,构造ATA\boldsymbol{A}^\text{T}\boldsymbol{A}ATA及ATb\boldsymbol{A}^\text{T}\boldsymbol{b}ATb,然后调用博文《线性方程组的通解》定义的mySolve函数,解方程组ATAxATb\boldsy…
线性代数Python计算:正交向量组的扩张
已知α1(a11a12⋮a1n),α2(a21a22⋮a2n),⋯,αk(ak1ak2⋮akn)∈\boldsymbol{\alpha}_1\begin{pmatrix}a_{11}\\a_{12}\\\vdots\\a_{1n}\end{pmatrix},\boldsymbol{\alpha}_2\begin{pmatrix}a_{21}\\a_{22}\\\vdots\\a_{2n}\end{pmatrix},\cdots,\boldsymbol{\alpha}_k\begin{pm…
线性代数Python计算:向量空间坐标变换
向量空间中两组基AAA和BBB之间相互线性表示构成的矩阵为过渡阵。若两组基中之一为自然基,譬如AAA为自然基,则基BBB的各向量在自然基下的坐标即构成基AAA到基BBB的过渡阵P\boldsymbol{P}P。否则,找到自然基到基AAA的过渡阵A\boldsymbol{A}A&am…
5003笔记 Statistic Chapter2-Regression and Smoothing
回归就是让每个点到回归线的距离尽可能短。 注意ε是误差值,满足norm(0,1)分布,ε会让我们的预测增加不确定性,但是会让我们预测准确度上升。防止模型过拟合。
这里老师是用Residual sum of squares来解释的最小二乘。邹博老师在机器学习里是…
[解题报告]《算法零基础100讲》(第3讲) 矩阵
☘前言☘
今天是九日集训第七天,我会记录一下学习内容和题解,争当课代表0.0. 链接:《算法零基础100讲》(第3讲) 矩阵 🧑🏻作者简介:一个从工业设计改行学嵌入式的年轻人 ✨联系方式:2201891280…
线性代数学习笔记(十八)——矩阵的秩(一)
本篇笔记先回顾了k阶子式的定义,并计算各子式的值;然后引出了矩阵秩的定义,即矩阵的秩是非零子式的最高阶数;还通过不同结构图形分类的方式来类比矩阵秩的概念。
1 kkk阶子式 kkk阶子式:给定一个矩阵,任取…
线性代数学习笔记(十七)——初等变换(三)
本篇笔记首先回顾了伴随矩阵法求逆矩阵,因为过程过于复杂,所以引出初等变换法求逆矩阵,并推导了初等变换法求逆矩阵的思路;然后通过一个例子介绍了初等变换法求逆矩阵的过程,并对注意事项进行了总结;最后还…
线性代数学习笔记(十四)——分块矩阵
本篇笔记首先介绍了分块矩阵的概念,并介绍了按行或按列进行分块的两种常见分块方式,还讨论了矩阵标准形的主要基本特征,然后重点讨论了分块矩阵的几种运算,包括分块矩阵的和、差、数乘和乘积,以及对角型分块矩阵、三角…
[现代控制理论]9_状态观测器设计_龙伯格观测器
[现代控制理论]11_现代控制理论串讲_完结_pdf获取 [现代控制理论]10_可观测性与分离原理_观测器与控制器 [现代控制理论]9_状态观测器设计_龙伯格观测器 [现代控制理论]8.5_线性控制器设计_轨迹跟踪simulink [现代控制理论]8_LQR控制器_simulink [现代控制理论]7_线性控制器设计…
机器学习中的数学知识——最小二乘法
1.线性回归 2.非线性回归 3.聚类 4.分类 5.降维 6.优化算法(启发式优化算法)
定义
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据&…
机器学习中的数学知识3——特征值分解
特征值与特征向量
定义
在线性代数中,对于给定的线性变换A\mathbf AA,它的特征向量vvv经过这个线性变换的作用之后,得到的新的向量仍然与原来的vvv保持在同一条直线上。但其长度或许会改变。即Avλv\mathbf Av\lambda vAvλv 其中λ\lambda…
线性代数学习笔记(五)——行列式的计算(一)
本篇笔记介绍行列式的计算方法,如果行列式中的0比较少,一般先使用行列式的性质(常用性质2和性质7)将其化成上三角行列式。尽量将左上角元素先变为1或-1,避免出现分数。求余子式或代数余子式时,往往需要构造…
计算机视觉学习3:矩阵基础
首先我们来讲一讲placehold: placehold的特点在于它只定义,不初始化,就像是把常数放到了变量的地位,也要自己初始化了。那要怎样初始化呢?要在sess.run()里面,开始要实际操作了的时候进行初始化。在自己要运行的东西&a…
逻辑代数:逻辑运算与定理,代数化简
公理: 基本定理: 交换律,结合律自不必说,分配律你见过吗?: 好像把与变成或,或变成与对等式不影响?没错,这叫对偶式: 注意不要改优先级。可以用括号。 还有更多…
算法设计学习:数学基础
表示算法效率的方法:增长率。
计算方法:不要低阶项和常数项,只要高阶项。
同阶函数:
(g(n)){f(n) | 存在c1, c2>0, n0, 任意n>n0, c1g(n)<f(n)<c2g(n)}
称为与g(n)同阶的函数集合。 证明用定义,就像…
数论_欧拉函数_快速幂_欧几里得_逆元_素数筛
数论的一些基本知识欧拉函数欧拉函数的基本概念欧拉函数的性质求欧拉函数值快速幂题目背景欧几里得算法(辗转相除法)求最大公因数扩展欧几里得算法算法描述代码实现扩展欧几里得算法的一些应用计算乘法逆元的代码素数筛欧拉函数
欧拉函数的基本概念
对…
算法R2D8-复习一维前缀和二维前缀和
一维前缀和
前缀和主要是把一个序列求和的问题从O(n)降到O(1)。预处理还是O(n)的。 注意: 前缀和下标从1开始,为了规范化所有查询。 可以在数组本身上进行累加,不用重新…
DW李宏毅机器学习Task5
1、当梯度很小时,优化效果没有达到期望
Optimization失败的原因:(1)local minimum;(2)saddle point(鞍点) gradient为0,会导致loss不下降,即卡…
MATLAB----输入和输出
文章目录1. 输入语句1.1 输入数值或矩阵1.2 输入字符串2. 输出语句2.1. 输出单个字段2.2. 输出多个字段1. 输入语句
1.1 输入数值或矩阵
value1 input("请输入一个数值:")
value2 input("请输入一个矩阵:")1.2 输入字符串
输入…
利用matlab编程,用 Jacobi选代法与 Gauss Seide选代法解下列方程组:x+2y-2z=6,x+y+z=6,2x+2y+z=11
这是方程组的系数矩阵形式: [ 2 -2 -2 ] [ x ] [ 6 ] [ 1 1 0 ] [ y ] [ 6 ] [ 2 0 1 ] [ z ] [ 11 ] 首先,我们可以使用Jacobi迭代法来求解方程组。 步骤如下: 初始化迭代计数器和迭代终止阈值。 设置初始猜测值 x0, y0, z0。 对于每一个未…
超强换元法,二重积分计算的利器(雅可比行列式超通俗讲解)
二重积分计算是个老大难,有的题目计算过程极其复杂,直角坐标和极坐标换元已不足以应对“复杂路况”,这个时候怎么办?整上一手超强换元法,出奇制胜,本文带你一窥究竟。 首先来回顾下定积分的换元过程&#x…
【Numpy学习】第四节 Numpy线性代数相关
Numpy 定义了 matrix 类型,使用该 matrix 类型创建的是矩阵对象,它们的加减乘除运算缺省采用矩阵方式计算,因此用法和Matlab十分类似。但是官方并不推荐在程序中使用 matrix,所以仍然用 ndarray 来介绍。 文章目录0. 思维导图总结1. np中的广…
抖音矩阵号/抖音短视频SEO矩阵系统源码开发及开发者思路分享....
抖音矩阵号短视频系统,抖音矩阵号系统源码开发,思路分享,说一点开发者掏心窝子的话......
一套优秀的短视频获客系统,支持短视频智能剪辑、短视频定时发布,短视频排名查询及优化,短视频智能客服等,那么短视…
抖音seo账号矩阵系统源码代开发组件
一.开发矩阵系统的项目背景:
目录
一.开发矩阵系统的项目背景:
二.短视频矩阵系统SaaS模板组件通常包含以下几个方面的内容:
三.抖音SEO账号矩阵系统源码的技术搭建过程可以分为几个步骤:
1.确定系统的需求和目标,…
《深度学习》数学知识基础
由于之前我学习过高等代数和解析几何,所有在此只列举不熟悉或容易忘记的知识点。目录如下: 一、 线性代数 二、概率与信息论 三、数值计算
一、线性代数
张量:一般的,一个数组中的元素分布在若干维坐标的规则网格中,…
【优化求解】遗传算法求解峰谷分时电价电动汽车充电负荷优化问题【含源码 210期】
一、代码运行视频(哔哩哔哩)
【优化求解】遗传算法求解峰谷分时电价电动汽车充电负荷优化问题【含源码 210期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]欧名勇,陈仲伟,谭玉东,文明,周志成.基于峰谷分时电价引导下的电动汽车充电…
MATLAB----变量类型和转化
文章目录1. 数值类型2. 字符串类型2.1. 字符串可以为矩阵的元素2.2. 字符串的拼接3. 字符串和数值的转化3.1. 字符串转为数值3.2. 数值转为字符串1. 数值类型
double类型,可以组成数值和数值矩阵,可以进行加减乘除逻辑运算。
a 1
b [1 2]2. 字符串类…
【Matlab路径规划】蚁群算法求解机器人栅格地图最短路径规划问题【含源码 1580期】
一、代码运行视频(哔哩哔哩)
【Matlab路径规划】蚁群算法求解机器人栅格地图最短路径规划问题【含源码 1580期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]姚晓通,李致远,程晓.基于改进蚁群算法的机器人路径规划研究[J]. 计算机仿…
【Matlab优化选址】禁忌搜索算法求解基站选址优化问题【含源码 440期】
一、代码运行视频(哔哩哔哩)
【Matlab优化选址】禁忌搜索算法求解基站选址优化问题【含源码 440期】
二、matlab版本及参考文献
1 matlab版本 2014a
2 参考文献 [1]陈煜婷,张惠珍.双层级医疗设施选址问题及禁忌搜索算法[J]. 运筹与管理. 2021,30(09)…
链表实现多项式加法与乘法
链表实现加法与乘法
构建一个链表
typedef struct LinkNode{int coef;//系数int expn;//幂指数LinkNode *next;
}LinkNode,*LinkList;为了使得直接可以更好的查看输出结果,顺便写一个show函数用来展示结果
void show(LinkList L){//输出多项式链表结点ÿ…
水桶分水问题详解(C++实现)
发呆——尽量用最简单的话语让读者理解问题思路,让读者不在发呆 Talk is cheap, show me the code . 你知道的越多,你不知道的越多。 如有什么建议或者不足欢迎大佬评论区或者私信指出 两水桶分水 三水桶分水 N水桶分水 两水桶分水
如果你有无穷多的水&…
MATLAB散点图形式绘制爱心曲线
>> t 0:pi/50:2*pi;
>> x 16*sin(t).^3;
>> y 13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t);
>> scatter(x,y,rd,filled)运行结果:
RNS (Residue Number System) 剩余数系统
RNS(Residue Number System)介绍
目前RNS并没有一个正式的中文名,若有,请各位大佬指正。
简介
简而言之,剩余数系统就是将一个大一点的数A∈ZQA\in \mathcal{Z}_QA∈ZQ,用好几个小一点的数来表示:A←{…
Markdown 快速入门(Typora)
Markdown 快速入门(Typora)
第一部分 基础
1.1 标题
# 一级标题
## 二级标题
### 三级标题
...
###### 六级标题
或者快捷键
Ctrl1 一级标题
Ctrl1 二级标题
...
Ctrl6 六级标题1.2 字体
*斜体* 或者Ctrl i
**加粗** 或者Ctrl b
***加粗斜体***…
随机数的生成矩阵的运算2numpy的索引
import numpy as npsample np.random.random((3,2))
#生成3行2列由0-1的随机数组成的数组
print(sample)sample np.random.normal(size(3,2))
#生成3行2列由符合标准正态分布随机数组成的数组
print(sample)sample np.random.randint(0,10,size(3,2))
#生成3行2列由0-10随机…
程序员的自我修养之数学基础03:矩阵的意义和运算
什么是矩阵?
按照课本上的定义: 矩阵就是由m行n列数放在一起组成的数学对象。 或者更简单一点: 把数列排成矩形,就是矩阵。 对于一个n行m列的矩阵,我们把它叫做一个nm矩阵。当矩阵的行数和列数相同时,我们…
图形学 View矩阵的构造
经常遇到View矩阵的构造,现在记下来彻底弄明白吧 参考: https://gameinstitute.qq.com/community/detail/117006 左右手坐标系:https://www.3dgep.com/3d-math-primer-for-game-programmers/ 目的
模型和视图变换阶段分为模型变换和视图变换。模型变换的…
Fibonacci 第 n 项
这题是因为数据量很大,到了后面数组就没有办法保存斐波那契数了
考虑12的矩阵【 f [ n − 2 ] , f [ n − 1 ] 】。根据fibonacci数列的递推关系,我们希望通过乘以一个2 2 的矩阵,得到矩阵【 f [ n − 1 ] , f [ n ] 】 【 f [ n − 1 ] ,…
线性代数Python计算:解可逆系数矩阵线性方程组
numpy的linalg模块中solve函数解可逆系数矩阵的线性方程组。该函数的调用接口为 solve(A, b)\text{solve(A, b)}solve(A, b) 参数A表示系数矩阵A\boldsymbol{A}A,b表示常数矩阵b\boldsymbol{b}b。若A表示的系数矩阵可逆,返回方程组Axb\boldsymbol{Ax}\bo…
线性代数学习笔记(十三)——逆矩阵(二)
本篇笔记首先回顾了伴随矩阵,随后给出了逆矩阵的定义,并通过定理给出了采用伴随矩阵法求逆矩阵的公式以及推论,由于伴随矩阵法求逆矩阵计算量过于复杂,一般不常用,更常用的方法是后续介绍的初等变换法;使用…
线性代数学习笔记(十)——矩阵运算(二)
本篇笔记讲解矩阵的幂运算和矩阵的转置,其中矩阵进行幂运算的前提是矩阵为方阵,矩阵幂运算的两条性质与数的幂运算规则类似;矩阵转置的定义与行列式转置类似,但要注意由于矩阵的行数和列数不同,所以转置之后行数和列数…
线性代数学习笔记(八)——矩阵概念
本笔记通过航班信息和人际关系的图表引入矩阵的定义,探讨了矩阵和行列式的关系,并给出了矩阵相关概念的说明,例如实矩阵、复矩阵、行矩阵、列矩阵、零矩阵、负矩阵、方阵、单位阵和同型矩阵等。
1 举例
航班信息: 假设有以下三个…
线性代数学习笔记(二)——n阶行列式
通过分析三阶行列式每项的符号与列标排列、逆序数和奇偶性的关系,推广得到n阶行列式的第一种定义(按行展开)。然后分析了几种特殊的行列式:下三角行列式、上三角行列式、对角型行列式以及对应三种“山寨版”的行列式,并…
二维快速傅里叶逆变换
ifft2二维快速傅里叶逆变换全页折叠语法X ifft2(Y)X ifft2(Y,m,n)X ifft2(___,symflag)说明示例X ifft2(Y) 使用快速傅里叶变换算法返回矩阵的二维离散傅里叶逆变换。如果 Y 是一个多维数组,则 ifft2 计算大于 2 的每个维度的二维逆变换。输出 X 的大小与 Y 相同…
暴力完全遍历(回溯法)-任意n位数的全排列
暴力完全遍历(回溯法)
应用情形:算式中A-I分别代表1-9的数字,不同的字母代表不同的数字,其满足如下算式: 比如68/3952/714和53/1972/486就是其中的两组解 问:该算式共有多少种解法
分析&…
pytorch规约计算(累和、累积、均值、方差、标准差、P范数等)
目录一、什么是规约计算?1.累积、累和、所有元素的乘积、所有元素的和2.p-norm距离3.均值、中位数、众数、方差和标准差一、什么是规约计算?
一般是指分组聚合计算,常见的由均值、方差等,该计算的特点是使分组内或所有的元素参与…
【KITTI】Kitti数据集 Tr(旋转平移)矩阵求逆
本节详细介绍KITTI从图像坐标系到激光雷达坐标系的变换原理、过程和代码。 Kitti数据集的Tr_velo_to_cam矩阵是将激光雷达点云坐标变换到图像坐标系。Tr是一个3x4的矩阵,直接左乘激光雷达坐标即可得到图像坐标系中的坐标。 Tr可以认为是由旋转矩阵R和平移矩阵T组成&…
R语言中的函数11:corrplot::corrplot()和corrplot.mixed()
文章目录corrplot()介绍用法实例:corrplot.mixed()用法实例corrplot()
介绍
该函数实现了对correlation矩阵和置信区间的图示化。并且它也可以对一般的矩阵实现可视化只需要设置is.corr FALSE.
用法
corrplot(corr,method c("circle", "square…
指数分布族与广义线性模型
文章目录指数分布族的定义自然参数形式1性质自然参数形式2性质可识别性巴苏定理广义线性模型总结指数分布族的定义
如果{Pθ:θ∈Θ}\{P_\theta: \theta\in\Theta\}{Pθ:θ∈Θ}是关于σ−\sigma-σ−有限测度ν\nuν定义在(Ω,F)(\Omega, \mathcal{F})(Ω,F)上的分布族&…
当前有一个vtk格式的三维牙模数据,如何根据模型的顶点来创建邻接矩阵
如果您已经成功地读取了 VTK 格式的三维牙模数据,并已将其转换为顶点和面的形式,则可以使用以下方法创建邻接矩阵: 首先,根据模型的顶点数创建一个 N x N 的矩阵,其中 N 是顶点的数量。 然后,遍历每个面&am…
线性代数克莱姆法则的几何含义
以二元一次方程组的求解为例: { a c a 1 b c b 1 c 1 a c a 2 b c b 2 c 2 \left\{\begin{array}{l} a_{c}a_{1} b_{c}b_{1} c_{1} \\ a_{c}a_{2} b_cb_{2} c_{2} \end{array}\right. {aca1bcb1c1aca2bcb2c2
其中 a c a_c ac和 b c b_…
数值计算(一):引论
因为笔者最近在复习数值计算,所以开一个数值计算的版块 数值计算:为数学的一个分支,是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科。它以数字计算机求解数学问题的理论和方法为研究对象,为计算数学的主体部分。…
ICE-BA代码解析
从main函数开始,读取左右相机,IMU的配置文件,加载左相机和右相机的图像列表,然后进入循环处理依次处理每一帧图像并跟踪特征点,特征点跟踪使用的Brisk库,和通用的跟踪过程相似,我们主要关注特征…
TEM波以及TEM TE TM模的区别
补一下我之前在博客园发布的内容 TEM波就是横波,HxE与k三者相互垂直,其他方向都没有分量
但有的在波传播方向k上有H波或E波,这就产生了所谓的TE波或TM波 TEM TE TM模的区别:
在自由空间传播的均匀平面电磁波(空间中没有自由电荷,没有传导电流),电场和磁场都没有和波传播方向平…
斐波那契数列(兔子生长案例)
斐波那契数列1. 题目2. 斐波那契数列在百度的解释3. 小编自己的理解(重点,因为简单)4. 实现程序的思路5. 代码实现嗨,大家好啊!!!开始前小编建议『
先看目录』今天想给大家分享的『
内容』是&am…
普利姆算法--求最小生成树
在普里姆算法中,我们从一些根顶点开始的单个集群生成一颗最小生成树,主要思想与Dijkstra算法一些,属于贪心算法
算法思想
我们先初始定义一个顶点,然后在相邻的所有边中迭代算这一个最小权值的边 e (u,v),将顶点u链…
双(2-(3,5-二甲基苯基)喹啉-C2,N‘)(乙酰丙酮)合铱(III),cas:1056874-46-4,齐岳金属配合物材料
双(2-(3,5-二甲基苯基)喹啉-C2,N)(乙酰丙酮)合铱(III),cas:1056874-46-4,齐岳金属配合物材料
中文名称: 双(2-(3,5-二甲基苯基)喹啉-C2,N)(乙酰丙酮)合铱(III)
中文同义词: 双(2-(3,5-二甲基苯基)喹啉-C2,N)(乙酰丙酮)合铱(III) 1G;双(2-(3…
机器学习算法基础:硬核高斯分布
提前放狠话:看不懂打si我吧,真的很细节了。 提前了解: 1、极大似然估计(MLE)、最大后验概率估计(MAP)、贝叶斯估计区别 2、正定矩阵与半正定矩阵定义性质与理解 3、马氏距离和欧式距离详解 4、参…
非线性规划转化为线性规划问题(司守奎老师数模例题)-------数模学习笔记一
目录一、非线性问题1.问题描述与分析2.问题解决思路二、具体求解步骤1.引入ui与vi变量2.引入变量后新方程3.matlab程序总结本文主要记录司守奎数模书中第一章所给例题 提示:以下是本篇文章正文内容,下面案例可供参考
一、非线性问题
1.问题描述与分析 …
线性代数(三) 线性方程组
前言
如何利用行列式,矩阵求解线性方程组。
线性方程组的相关概念 用矩阵方程表示
齐次线性方程组:Ax0;非齐次线性方程组:Axb. 可以理解 齐次线性方程组 是特殊的 非齐次线性方程组 如何判断线性方程组的解 其中R(A)表示矩阵A的…
Java计算两个经纬度坐标之间的距离
/*** 计算两个经纬度坐标之间的距离* param lng1: 第1个坐标的经度* param lat1: 第1个坐标的纬度* param lng2: 第2个坐标的经度* param lat2: 第2个坐标的纬度* return*/public static double getDistance(double lng1,double lat1,double lng2,double lat2){return (111120 …
【每日一题】1572. 矩阵对角线元素的和
【每日一题】1572. 矩阵对角线元素的和 1572. 矩阵对角线元素的和题目描述解题思路 1572. 矩阵对角线元素的和
题目描述
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例 1&a…
5.利用matlab完成 符号矩阵的转置和 符号方阵的幂运算(matlab程序)
1.简述 Matlab符号运算中的矩阵转置
转置向量或矩阵
B A. B transpose(A) 说明
B A. 返回 A 的非共轭转置,即每个元素的行和列索引都会互换。如果 A 包含复数元素,则 A. 不会影响虚部符号。例如,如果 A(3,2) 是 12i 且 B A.࿰…
LeetCode378之有序矩阵中第 K 小的元素(相关话题:优先队列,二分)
题目描述
给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。请注意,它是 排序后 的第 k 小元素,而不是第 k 个 不同 的元素。
示例 1:
输入:matrix [[1,5,9],[10…
4.利用matlab符号矩阵的四则运算(matlab程序)
1.简述 符号对象的建立 sym函数 sym函数用于建立单个符号对象,其常用调用格式为: 符号对象名sym(A) 1 将由A来建立符号对象,其中,A可以是一个数值常量、数值矩阵或数值表达式(不加单引号),此时符号对象为一个符号常量;…
【LeetCode 算法】Matrix Diagonal Sum 矩阵对角线元素的和
文章目录 Matrix Diagonal Sum 矩阵对角线元素的和问题描述:分析代码Math Tag Matrix Diagonal Sum 矩阵对角线元素的和
问题描述:
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不…
一文通俗搞懂线性无关特征向量个数≤特征值重数
线代有个很难理解的知识点,即同一特征值的线性无关特征向量个数要小于等于特征值重数。 这个结论是怎么来的呢?本文用最朴素的证明来帮助大家弄懂这个知识点(结论推导所用的都是基础的线代知识,只是有些数学式子比较复杂ÿ…
rank(A)=rank(A^TA)
Let x∈N(A)x\in N(A)x∈N(A) where N(A)N(A)N(A) is the null space of AAA. Hence Ax0⇒ATAx0⇒x∈N(ATA)Ax0 \Rightarrow A^TAx0 \Rightarrow x\in N(A^TA)Ax0⇒ATAx0⇒x∈N(ATA)
It means that N(A)⊂N(ATA)N(A)\subset N(A^TA)N(A)⊂N(ATA). On the other hand, suppose …
the-matrix-cookbook(1-0)
UTF8gbsn (AB)−1B−1A−1(\mathbf{A B})^{-1}\mathbf{B}^{-1} \mathbf{A}^{-1}(AB)−1B−1A−1 ABB−1A−1A(BB−1I)A−1AA−1IABB^{-1}A^{-1}A(BB^{-1}I)A^{-1}AA^{-1}IABB−1A−1A(BB−1I)A−1AA−1I,B−1A−1B^{-1}A^{-1}B−1A−1就是ABABAB的逆矩阵故而有(AB)−1B−1A−1(…
Lego-LOAM雅可比矩阵的推导
求解的问题是当前帧投影到上一帧中点到线的最小距离即F(X),因为优化R,T所以X{R,T}。
首先声明几个符号,为当前帧的点(在世界坐标系下的),为当前帧投影到上一帧中的点(lidar坐标系),为当前帧的点…
PCA(主成分分析法)的理解笔记及算法的实现
前几天搞定了Open3d库问题后,准备手撕PCA算法突然人麻了。我坚信学习是不断重复的过程,特此做个笔记,欢迎大家评论和交流!
感谢大佬的文章:
1、主成分分析(PCA)原理详解_Microstrong-CSDN博客…
2022数字逻辑笔记02
2022数字逻辑笔记01内容预览笔记笔记内容为日常上课记录与整理,为图片格式,仅供学习。 内容预览
1.逻辑函数及其表示方法 2.逻辑函数的两种标准形式 3.逻辑函数的公式法化简 4.卡诺图化简法 5.相关作业 6.包含无关项的逻辑函数的化简 7.本章小结 笔记 —…
SLAM中旋转向量(旋转轴/旋转角)、旋转矩阵、四元数、李代数的相互转化(附C++ Eigen库代码实例)
旋转轴/旋转角、旋转矩阵、四元数、李代数都可以表示旋转,那么这几者的转换是如何实现的呢?
绕一个轴,旋转角度的旋转,例如,在三维空间中,以为轴,旋转45,表示为,注意&am…
alpha-beta滤波
The alpha - beta - gamma filter
import numpy as np
import matplotlib.pyplot as plt
import randommid, sigma 0, 0.1
totalTimeStep 300
noise np.random.normal(mid, sigma, totalTimeStep) * 100dt 1
v 0
x_lf 0
# 测量值
x 0
x_lf_list []
x_list []
# 估计值…
13-把矩阵看作是对系统的描述
探索矩阵乘法:更深刻的理解与应用视角 🧩🔍
引言 📖
在我们进一步探讨矩阵乘法之前,让我们从不同的角度来理解什么是矩阵,以及如何将矩阵视为一个系统。我们之前已经介绍了矩阵的基本概念和运算ÿ…
【考研数学】线形代数第三章——向量 | 3)向量秩的性质、向量空间、过渡矩阵
文章目录 引言三、向量组等价、向量组的极大线性无关组与秩3.2 向量组秩的性质 四、 n n n 维向量空间4.1 基本概念4.2 基本性质 写在最后 引言
紧接前文学习完向量组秩的基本概念后,继续往后学习向量的内容。 三、向量组等价、向量组的极大线性无关组与秩
3.2 向…
将正方形矩阵顺时针转动 90°
将正方形矩阵顺时针转动 90
【题目】
给定一个 NN 的矩阵 matrix,把这个矩阵调整成顺时针转动 90后的形式。 例如: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 顺时针转动 90后为: 13 9 5 1 14 10 6 2 15 11 7 3 16 12 8 4
【要求】
额外空…
线性代数(三) 线性方程组向量空间
前言
如何利用行列式,矩阵求解线性方程组。
线性方程组的相关概念 用矩阵方程表示
齐次线性方程组:Ax0;非齐次线性方程组:Axb. 可以理解 齐次线性方程组 是特殊的 非齐次线性方程组 如何判断线性方程组的解 其中R(A)表示矩阵A的…
Gephi国家政策文本关键词共现矩阵的共现网络图分析
文章目录 分词jieba分词关键词提取python处理形成共现矩阵gephi导入共现矩阵过滤边的权重进行优化最终效果分词
本文研究不同文章中的关键词出现次数,因此将出现在同一篇文章中的关键词都定义为”共现”。
jieba分词
对不同后缀文件(txt、docx、pdf)进行不同处理,提取文…
【1572. 矩阵对角线元素的和】
来源:力扣(LeetCode)
描述:
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。
示例 1:
输入:mat [[1,2,3]…
6.利用matlab完成 符号矩阵的秩和 符号方阵的逆矩阵和行列式 (matlab程序)
1.简述 利用M文件建立矩阵 对于比较大且比较复杂的矩阵,可以为它专门建立一个M文件。下面通过一个简单例子来说明如何利用M文件创建矩阵。 例2-2 利用M文件建立MYMAT矩阵。(1) 启动有关编辑程序或MATLAB文本编辑器,并输入待建矩阵:(2) 把…
9.利用matlab完成 泰勒级数展开 和 符号表达式傅里叶变换和反变换 (matlab程序)
1.简述 matlab之傅里叶变换和逆变换 首先生成一个方波(或者其他组合波形),然后对这个信号做傅里叶变换,拆解到频域,可以看到这个信号是由哪些频率的信号叠加而来。
然后把频域信号,用傅里叶逆变换恢复到时…
散度和KL散度的介绍
散度和KL散度的介绍
1. 梯度、散度与旋度
1.1 算子
定义一个向量算子∇\nabla∇(读作nabla或者del): ∇∂∂xex⃗∂∂yey⃗∂∂zez⃗(1.1)\nabla \frac{\partial}{\partial x} \vec{e_x} \frac{\partial}{\partial y} \vec{e_y} \frac{\partial}{\partial z} \…
MIT 线性代数(31—33)读书笔记
第三十一讲:线性变换及对应矩阵
本讲从线性变换这一概念出发,每个线性变换都对应于一个矩阵。矩阵变换的背后正是线性变换的概念。理解线性变换的方法就是确定它背后的矩阵,这是线性变换的本质
1 线性变换
1.1 定义 如何判断一个操作是不是…
MIT 线性代数(25—27)读书笔记
第二十五讲:复习二
1.第14到24讲总结 我们学习了正交性(正交向量和正交补),有矩阵Q[q1 q2 ⋯ qn]Q=\Bigg[q_1\ q_2\ \cdots\ q_n\Bigg],若其列向量相互正交,则该矩阵满足QTQI。进一步研究投影(…
MIT 线性代数(22—24)读书笔记
第二十二课时:对角化和A 的幂 本讲主要讲:Axλx,特征值、特征向量的应用以及为什么需要特征值和特征向量。 1.对角化矩阵
1.1 对角化的定义 上一讲我们提到关键方程Axλx,通过det(A−λI)0得到特征向量λ,再带回关键方程算出特征…
MIT 线性代数(19—21)读书笔记
第十九讲 行列式公式和代数余子式 1.行列式公式
上一讲中,我们从三个简单的性质扩展出了一些很好的推论,本讲将继续使用这三条基本性质: detI1;交换行行列式变号;对行列式的每一行都可以单独使用线性运算,…
MIT 线性代数(16—18)读书笔记
第十六讲 投影矩阵(Axb)和最小二乘法 上一讲中,我们知道了投影矩阵PA(ATA)−1ATPA(A^TA)^{-1}A^TPA(ATA)−1AT,PbPbPb将会把向量投影在AAA的列空间中。即只要知道矩阵AAA的列空间,就能得到投影矩阵PPP的导出式。 ##1.投影矩阵(Axb…
MIT 线性代数(13—15)读书笔记
第十三讲 第一阶段总结
前12讲主要是介绍了矩阵的基础知识、Ax0和Axb、四个空间(A的零空间、列空间、行空间和左零空间)。本讲主要是介绍了一些基本题目和简要定理。 第一题. 令u、v、w是R^7空间内的非零向量:则u、v、w生成的向量空间可能是…
MIT 线性代数(10—12)读书笔记
第十讲:四个基本子空间
假设A是mn,列空间C(A),零空间N(A),行空间C(A^T),A转置的零空间(通常叫左零空间)N(A^T),这是线性代数的核心内容,研究这四个基本子空间及其关系。我们从上一讲中的基、维…
线性代数(四) 特征值相似矩阵
前言
前面主要讲述的是方程组和矩阵的关系,现在了解下矩阵和矩阵的关系
方阵的特征值与特征向量
假设A为n阶方阵,对于一个数 λ \lambda λ
若存在:非零列向量 α \alpha α,使得: A α ⃗ λ α ⃗ A\vec{\alp…
MIT 线性代数(7—9)读书笔记
---------------------------------------------------------------------------------------------------------------------
第七讲 求解Ax0:主变量、特解
本课时将讲解如何计算那些向量空间中的向量,从概念定义转向算法,求解Ax0的算法…
MIT 线性代数(1—3)读书笔记
几年前把MIT Gilbert Strang教授的线性代数看完了,不过没做笔记,很多东西都忘了,现在打算重新看一遍,边写边做笔记。不足之处请指教。
--------------------------------------------------------------------------------------…
DevCpp和VS2019安装armadillo库
DevCpp中
点这里下载armadillo 然后解压出来一个文件夹"armadillo-10.4.0",
找到include 看到这两项,就是我们要copy的
找到你DevCpp安装的位置
这里我装的是MinGW,如果你的是TDM-GCC同理 点开编译器的include文件夹
把我们解压出来…
eg 6-9 Multi-dimensional array names as function arguments
/*求3*4矩阵的转置矩阵
*/#include <stdio.h>#define M 3
#define N 4void reverse(int x[][N],int y[][M]) //求x矩阵的转置矩阵y,形参数组的第一维大小说明可以省略,第二维不能省
{int i,j;for(i0;i<N;i) //矩阵转置for(j0;j<M;…
每日编程一刷--矩阵初等行变换你会了吗?
文章目录每日编程一刷--矩阵初等行变换你会了吗?前言总结每日编程一刷–矩阵初等行变换你会了吗?
前言
欢迎来到每日编程一刷 基础
相信大家学了一天的高数 现代 大学生应该都是考试周了 你真的将现代知识掌握了没有
下面靠一靠大家 错误代码 以及思…
7.利用matlab完成 符号方阵的特征值分解和 符号矩阵的奇异值分解 (matlab程序)
1.简述 (1)特征值分解:函数eig 格式:[V,D] eig(A) %计算A的特征值对角阵D和特征向量V,使AVVD成立。
注意:特征值分解时,使用eig,矩阵A必须是方阵。
A [0 1;1 1]; [V,D] ei…
第七章,相似矩阵及其应用,2-实对称矩阵之相似对角化
第七章,相似矩阵及其应用,2-实对称矩阵之相似对角化 实对称矩阵的性质实对称矩阵对角化定理对称矩阵对角化步骤 玩转线性代数(35)实对称矩阵之相似对角化的笔记,相关证明以及例子见原文 实对称矩阵的性质
实对称矩阵在特征值与特征向量方面有…
LA@2@1@线性方程组和简单矩阵方程有解判定定理
文章目录 矩阵方程有解判定定理线性方程组有解判定特化:齐次线性方程组有解判定推广:矩阵方程 A X B AXB AXB有解判定证明推论 矩阵方程有解判定定理
线性方程组有解判定 线性方程组 A x b A\bold{x}\bold{b} Axb有解的充分必要条件是它的系数矩阵A和增广矩阵 ( A , b ) (A,…
LeetCode 热题 100(四):48. 旋转图像、240. 搜索二维矩阵 II、234. 回文链表
一.48. 旋转图像
题目要求:就是一个顺时针的旋转过程。 思路:观察矩阵,得出翻转前第i行的第J个元素 等于 翻转后倒数第i列的第J个元素,举例说明,第1行第2个元素为“2”,翻转后到了 倒数第1列的第2个元素…
【算法题】螺旋矩阵IV (求解n阶折线蛇形矩阵)
一、问题的提出
n阶折线蛇形矩阵的特点是按照图1所示的方式排列元素。n阶蛇形矩阵是指矩阵的大小为nn,其中n为正整数。
题目背景
一个 n 行 n 列的螺旋矩阵可由如图1所示的方法生成,观察图片,找出填数规律。填数规则为从 1 开始填到 nn。 …
LA@n维向量@解析几何向量和线性代数向量
文章目录 概念n维向量向量类型实向量和复向量行向量和列向量行列向量的转换特殊向量向量运算 矩阵的向量分块👺 解析几何向量和线性代数向量👺向量空间 n n n维向量空间 n n n维空间的 n − 1 n-1 n−1维超平面 概念
n维向量
由 n n n个有次序的数 a …
抖音短视频SEO矩阵系统源码开发
一、概述
抖音短视频SEO矩阵系统源码是一项综合技术,旨在帮助用户在抖音平台上创建并优化短视频内容。本文将详细介绍该系统的技术架构、核心代码、实现过程以及优化建议,以便读者更好地理解并应用这项技术。 二、技术架构
抖音短视频SEO矩阵系统采用前…
机器学习笔记 | Linear Algebra Review(复习线性代数)
1、矩阵和向量(Matrices and Vectors) 上面矩阵A是一个4 x 2矩阵,Aij ,下标i j分别对应矩阵的第i行和第j列 。 一个有n行的向量被称为n维向量。
vi表示向量第i行中的元素。
一般情况下,所有的向量和矩阵都是从1-开…
运用谱分解定理反求实对称矩阵
文章目录 谱分解定理定理的运用 谱分解定理
设三阶实对称矩阵 A A A,若矩阵 A A A 的特征值为 λ 1 , λ 2 , λ 3 \lambda_1,\lambda_2,\lambda_3 λ1,λ2,λ3,对应的特征向量分别为 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α1,α…
(搜索) 剑指 Offer 12. 矩阵中的路径 ——【Leetcode每日一题】
❓剑指 Offer 12. 矩阵中的路径
难度:中等
给定一个 m * n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构…
员工矩阵号短视频saas管理系统---开发工具
一、短视频矩阵号系统源码开发层面如何来解决?
1.短视频矩阵号系统源码搭建中,首先开发者需要保证api接口的稳定性 ,保证权限应用场景满足官方平台的开发预期。api---待发布、用户管理与授权绑定、私信回复与评论管理等是非常重要的权限接口…
【Math】特征值和奇异值辨析
奇异值和特征值都描述了一个矩阵的一些特性,但很多情况下,对于两者之间的区别和联系都不太清楚。
本文就这两者进行解析,并对奇异值的一些简单应用进行探索。 奇异值与特征值的定义
奇异值与特征值都被用于描述矩阵作用于某些向量的标量&am…
第五章,向量空间,2-基变换与坐标变换
第五章,向量空间,2-基变换与坐标变换 定理 (唯一表示定理)证明唯一性 坐标变换 玩转线性代数(27)基变换与坐标变换的笔记,相关证明以及例子见原文 定理 (唯一表示定理)
令 B { b 1 , b 2 , ⋯ , , b r } B\{b_1,b_2,\cdots,,b_r\} B{b1,b…
第五章,向量空间,3-内积、长度、夹角和距离
第五章,向量空间,3-内积、长度、夹角和距离 内积定义内积的运算性质内积空间 长度性质单位向量及单位化 夹角距离 玩转线性代数(28)长度、夹角和距离的笔记,相关证明以及例子见原文 内积
定义
设有n维向量 x ( x 1 x 2 ⋮ x n ) , y ( y…
第五章,向量空间,4-正交向量组
第五章,向量空间,4-正交向量组 正交标准正交基定义 正交向量组定理1正交基、标准正交基向量在标准正交基下的坐标标准正交化利用施密特(Schimidt)正交化法求标准正交基单位化 正交矩阵性质 正交变换 玩转线性代数(29)正交向量组的笔记,相关证…
线性代数的学习和整理5: 矩阵的加减乘除及其几何意义
目录
1 矩阵加法
1.1 矩阵加法的定义
1.2 加法的属性
1.2.1 只有同类型,相同n*m的矩阵才可以相加
1.2.1 矩阵加法的可交换律:
1.2.2 矩阵加法的可结合律:
1.3矩阵加法的几何意义
2 矩阵的减法
2.1 矩阵减法定义和原理基本同 矩阵的…
抖音短视频SEO矩阵系统源码开发及开发者思路分享......
抖音矩阵号/抖音短视频SEO矩阵系统源码开发及开发者思路分享: 短视频获客系统支持短视频智能剪辑、短视频定时发布,短视频排名查询及优化,智能客服等,那么短视频seo系统开发时需要开发哪些功能呢?今天我就跟大家分享一下我们的开发…
抖音seo短视频矩阵系统源码开发源代码分享--开源-可二开
适用于抖音短视频seo矩阵系统,抖音矩阵系统源码,短视频seo矩阵系统源码,短视频矩阵源码开发,支持二次开发,开源定制,招商加盟SaaS研发等。
功能开发设计
1. AI视频批量剪辑(文字转语音&#x…
Numpy入门(3)—线性代数
线性代数
线性代数(如矩阵乘法、矩阵分解、行列式以及其他方阵数学等)是任何数组库的重要组成部分,NumPy中实现了线性代数中常用的各种操作,并形成了numpy.linalg线性代数相关的模块。本节主要介绍如下函数:
diag&am…
使用ctcloss训练矩阵生成目标字符串
首先我们需要明确 c t c l o s s ctcloss ctcloss是用来做什么的。比如说我们要生成的目标字符串长度为 l l l,而这个字符串包含 k k k个字符,字符串允许的最大长度为 L L L,这里我们认为一个位置是一个时间步,就是一拍࿰…
线性代数(五) 线性空间
前言
《线性代数(三) 线性方程组&向量空间》我通过解线性方程组的方式去理解线性空间。此章从另一个角度去理解
空间是什么
大家较熟悉的:平面直角坐标系是最常见的二维空间 空间由无穷多个坐标点组成 每个坐标点就是一个向量
反过来,也可说&…
高等数学:线性代数-第三章
文章目录 第3章 矩阵的初等变换与线性方程组3.1 矩阵的初等变换3.2 矩阵的秩3.3 方程组的解 第3章 矩阵的初等变换与线性方程组
3.1 矩阵的初等变换
矩阵的初等变换 下面三种变换称为矩阵的初等变换
对换两行(列),记作 r i ↔ r j ( c i …
线性代数的学习和整理11: 子式与余子式
目录
1 原始矩阵A
2 子式(都是行列式)
2.1 k阶子式
2.2 k阶主子式
2.3 k阶顺序主子式
3 余子式
3.1 余子式
3.2 代数余子式
3.3 余子式作用是? 1 原始矩阵A
下面设计一个原始矩阵A,故意设计为A34, 行数≠列数
$$ \lef…
高等数学:线性代数-第二章
文章目录 第2章 矩阵及其运算2.1 线性方程组和矩阵2.2 矩阵的运算2.3 逆矩阵2.4 Cramer法则 第2章 矩阵及其运算
2.1 线性方程组和矩阵 n \bm{n} n 元线性方程组 设有 n 个未知数 m 个方程的线性方程组 { a 11 x 1 a 12 x 2 ⋯ a 1 n x n b 1 a 21 x 1 a 22 x 2 ⋯ a …
矩阵与图的关系:矩阵是图,图是矩阵
原文连接
线性代数最被低估的一个事实:矩阵是图,图是矩阵。 将矩阵编码为图是一种取巧的行为(cheat code),它其使复杂的行为变得易于研究。
让我告诉你怎么做!
1. 非负矩阵的有向图 (The directed graph of a nonne…
线性代数的学习和整理19,特征值,特征向量,以及引入的正交化矩阵概念
目录
1 什么是特征值和特征向量?
1.1 特征值和特征向量这2个概念先放后
1.2 直观定义
1.3 严格定义
2 如何求特征值和特征向量
2.1 方法1:结合图形看,直观方法求
2.1.1 单位矩阵的特征值和特征向量
2.1.2 旋转矩阵
2.2 根据严格定义…
Yalmip使用教程(6)-将约束条件写成矩阵形式
博客中所有内容均来源于自己学习过程中积累的经验以及对yalmip官方文档的翻译:https://yalmip.github.io/tutorials/ 这篇博客将详细介绍如何借助yalmip工具箱将约束条件写成矩阵形式。
1.相关函数介绍
1.1 depends和getvariables函数 depends和getvariables函数都…
线性空间、子空间、基、基坐标、过渡矩阵
线性空间的定义 满足加法和数乘封闭。也就是该空间的所有向量都满足乘一个常数后或者和其它向量相加后仍然在这个空间里。进一步可以理解为该空间中的所有向量满足加法和数乘的组合封闭。即若 V 是一个线性空间,则首先需满足: 注:线性空间里面…
WebGL矩阵变换库
目录
矩阵变换库:
Matrix4对象所支持的方法和属性如表所示:
方法属性规范: 虽然平移、旋转、缩放等变换操作都可以用一个44的矩阵表示,但是在写WebGL程序的时候,手动计算每个矩阵很耗费时间。为了简化编程…
「通信原理」格雷码的生成与破译
「通信原理」格雷码的生成与破译
格雷码,gray code,相邻两数之间只有一个bit发生了改变,因此相比于自然编码的二进制系统,格雷编码的更不容易出错。使用卡诺图化简布尔代数式的时候,也会用到格雷码。本文将介绍三种格…
线性代数(六) 线性变换
前言
《线性空间》定义了空间,这章节来研究空间与空间的关联性
函数
函数是一个规则或映射,将一个集合中的每个元素(称为自变量)映射到另一个集合中的唯一元素(称为因变量)。 一般函数从 “A” 的每个元…
【AI】数学基础——线代(向量部分)
参考: kenjihiranabe——The-Art-of-Linear-Algebra-zh-CN 详细计算方法与理论:见 矩阵论 线性代数的本质在于将具体事物抽象为数学对象,并描述其静态和动态特性 最基本的概念是 set 集合的定义是由某些具有某些共性的对象汇总成的集体。 将这…
线性代数的学习和整理18:什么是维度,什么是秩?秩的各种定理秩的计算 (计算部分未完成)
目录
0 问题引出:什么是秩?
概念备注:
1 先厘清:什么是维数?
1.1 真实世界的维度数
1.2 向量空间的维数
1.2.1 向量空间,就是一组最大线性无关的向量组/基张成的空间
1.3 向量α的维数
1.3.1 向量的…
计算机图形学线性代数相关概念
Transformation(2D-Model)
Scale(缩放) [ x ′ y ′ ] [ s 0 0 s ] [ x y ] (等比例缩放) \left[ \begin{matrix} x \\ y \end{matrix} \right] \left[ \begin{matrix} s & 0 \\ 0 & s \end{matrix} \right] \left[ \begin{matrix} x \\ y \en…
线性代数的学习和整理18:矩阵的秩的各种定理, 秩和维度(未完成)
目录
1 矩阵的秩
矩阵的秩
2 求秩的方法
矩阵的维度秩
矩阵的维度
向量的模,矩阵的模-没有把,难道是面积?
矩阵的平直概念
5 矩阵的初等变换(矩阵等价概念的引出) 1 为什么要引入矩阵的“秩” 这个概念&#x…
CCF CSP题解:矩阵运算(202305-2)
链接和思路
OJ链接:传送门
本题要求计算1个公式: ( W ⋅ ( Q K T ) ) V \left(\mathbf{W} \cdot (\mathbf{Q} \times \mathbf{K}^{T})\right) \times \mathbf{V} (W⋅(QKT))V 其中, Q \mathbf{Q} Q、 K \mathbf{K} K和 V \mathbf{V} V均…
【理解线性代数】(三)理解向量点乘
1. 向量点乘的几何含义
点乘的几何含义是初等数学中的知识,即点乘的几何含义是一个向量向另外一个向量上的投影的长度。计算公式为: a → ⋅ b → ∣ a ∣ ∣ b ∣ sin ( α ) \overrightarrow{a} \cdot \overrightarrow{b} \begin{vmatrix} a \e…
神经网络中的一些优化器整理
6 梯度平方的指数移动平均在神经网络优化中具有以下好处: 自适应学习率:梯度平方的指数移动平均允许每个参数的学习率自适应地调整。如果某个参数的梯度平方历史信息较大,那么其指数移动平均值会较大,从而减小学习率,使…
人工智能深度学习,100天掌握所有人工智能深度学习 –第二章:( 第 1 – 10 天第一节线性代数-线性方程组)
矩阵的迹:设A=[a ij ] nxn是n阶方阵,则对角元素之和称为矩阵的迹,记为tr(A)。tr(A) = a 11 + a 22 + a 33 + ……….+ a nn
矩阵迹的性质:设A和B为任意两个n阶方阵,则 tr(kA) = k tr(A) 其中 k 是标量。 tr(A+B) = tr(A)+tr(B) tr(AB) = tr(A)-tr(B) tr(AB) = tr(BA)…
numpy矩阵求MSE
MSE loss
#官方示例
from sklearn.metrics import mean_squared_error
y_true [[0.5, 1],[-1, 1],[7, -6]]
y_pred [[0, 2],[-1, 2],[8, -5]]
mean_squared_error(y_true, y_pred) #0.708验证
import numpy as np
A np.array(y_true)
B np.array(y_pred)mse (np.square…
15. 线性代数 - 克拉默法则
文章目录 克拉默法则矩阵运算Hi,大家好。我是茶桁。
上节课我们在最后提到了一个概念「克拉默法则」,本节课,我们就来看看到底什么是克拉默法则。
克拉默法则
之前的课程我们一直在强调,矩阵是线性方程组抽象的来的。那么既然我们抽象出来了,有没有一种比较好的办法高效…
线性代数的学习和整理20,关于向量/矩阵和正交相关,相似矩阵等(草稿)
目录
1 什么是正交
1.1 正交相关名词
1.2 正交的定义
1.3 正交向量
1.4 正交基
1.5 正交矩阵的特点
1.6 正交矩阵的用处 1 什么是正交
1.1 正交相关名词
orthogonal set 正交向量组正交变换orthogonal matrix 正交矩阵orthogonal basis 正交基orthogonal decompositio…
LA@向量组间的表示关系
文章目录 2个向量组间的表示关系向量组的相互表出向量组用另一个向量组表示👺线性表示的系数矩阵矩阵乘法与线性表出列向量组线性表示行向量组线性表示 向量组等价👺向量组等价的性质推论 等价矩阵与向量组等价的关系行等价矩阵的行向量组等价列等价矩阵…
【理解线性代数】(四)从向量组点乘到矩阵相乘
1. 批量化的发展趋势
工业生产的发展趋势总是从单件生产到批量生产。科学技术研究也是一样,总是从简单计算到复合运算、批量运算。批量意味着生产能力、处理能力的提升。计算机从16位发展到64位,从单核发展到多核;计算机从CPU处理数据发展到…
线性代数的本质(二)
文章目录 线性变换与矩阵线性变换与二阶方阵常见的线性变换复合变换与矩阵乘法矩阵的定义列空间与基矩阵的秩逆变换与逆矩阵 线性变换与矩阵
线性变换与二阶方阵
本节从二维平面出发学习线性代数。通常选用平面坐标系 O x y Oxy Oxy ,基向量为 i , j \mathbf i,…
矩阵论—线性子空间、生成子空间、核空间、零度、子空间的交与和、直和
线性子空间定义 如果,V1称为平凡子空间,否则称为非平凡子空间。
生成子空间 核空间、零度 解:
rank(A)2; n(A)N-rank(A)3-21,这里N表示的是未知量的个数。 n(A)也可以理解为基础解系的个数,即基础解系中有几个向量…
线性代数的本质(一)
文章目录 向量空间向量及其性质基与维数向量的坐标运算 《线性代数的本质》 - 3blue1brown 高中数学A版选修4-2 矩阵与变换 《线性代数及其应用》(第五版) 《高等代数简明教程》- 蓝以中 向量空间 In the beginning Grant created the space. And Grant said, Let there be vec…
17. 线性代数 - 矩阵的逆
文章目录 矩阵的转置矩阵的逆Hi, 您好。我是茶桁。
我们已经学习过很多关于矩阵的知识点,今天依然还是矩阵的相关知识。我们来学一个相关操作「矩阵的转置」,更重要的是我们需要认识「矩阵的逆」
矩阵的转置
关于矩阵的转置,咱们导论课里有提到过。转置实际上还是蛮简单…
59-代码随想录--数组--螺旋矩阵
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
模拟顺时针…
线性代数的本质(八)——内积空间
文章目录 内积空间内积空间正交矩阵与正交变换正交投影施密特正交化实对称矩阵的对角化 内积空间
内积空间
三维几何空间是线性空间的一个重要例子,如果分析一下三维几何空间,我们就会发现它还具有一般线性空间不具备的重要性质:三维几何空…
线性代数的本质(五)——矩阵的运算
文章目录 矩阵的运算矩阵的转置方阵的运算初等矩阵分块矩阵逆矩阵矩阵的秩广义逆矩阵 矩阵的运算
矩阵的转置
转置:矩阵 A A A的行列互换得到的矩阵称为 A A A 的转置(transpose),记作 A T A^T AT。
性质:矩阵转置运算满足下列性质&…
18. 线性代数 - 线性变换
文章目录 线性空间线性变换线性变换的几何意义特征值与特征向量NumPy的矩阵操作Hi, 你好。我是茶桁。
经历了几节线性代数课程之后,终于咱们到了最后一节课了。本节课的内容说多不多,说少也不少。
我们先是要理解一下线性空间和线性变换,并且探讨一下线性变换的几何意义。…
线性代数的本质(十一)——复数矩阵
文章目录 复数矩阵附录极大线性无关组向量叉积 复数矩阵
矩阵 A A A 的元素 a i j ∈ C a_{ij}\in\Complex aij∈C ,称为复矩阵。现将实数矩阵的一些概念推广到复数矩阵,相应的一些性质在复数矩阵同样适用。
定义:设复矩阵 A ( a i j…
线性代数的本质(二)——线性变换与矩阵
文章目录 线性变换与矩阵线性变换与二阶方阵常见的线性变换复合变换与矩阵乘法矩阵的定义列空间与基矩阵的秩逆变换与逆矩阵 线性变换与矩阵
线性变换与二阶方阵
本节从二维平面出发学习线性代数。通常选用平面坐标系 O x y Oxy Oxy ,基向量为 i , j \mathbf i,…
短视频seo矩阵系统源码开发搭建--代用户发布视频能力
短视频SEO矩阵系统源码开发搭建的代用户发布视频能力,主要是指在系统平台上,允许用户将其创作的内容发布到指定的账号或平台,并设置好相关的标题、话题、锚点等信息。 一、搭建步骤及注意事项
确定使用场景。根据业务需求,确定该…
经管博士科研基础【19】齐次线性方程组
1. 线性方程组 2. 非线性方程组
非线性方程,就是因变量与自变量之间的关系不是线性的关系,这类方程很多,例如平方关系、对数关系、指数关系、三角函数关系等等。求解此类方程往往很难得到精确解,经常需要求近似解问题。相应的求近似解的方法也逐渐得到大家的重视。
3. 线…
【算法练习Day2】有序数组的平方长度最小子数组螺旋矩阵II
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 有序数组的平方暴力求解…
【李沐深度学习笔记】线性代数实现
课程地址和说明
线性代数实现p2 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 这节就算之前内容的复习,后面以截图形式呈现
标量由只有一个元素的张量表示
import torch
x torch.tensor([3.0])
y …
保研CS/软件工程/通信专业问题汇总(搜集和自己遇到的)
机器学习
1.TP、TN、FP、FN、F1 2.机器学习和深度学习的区别和联系
模型复杂性:深度学习是机器学习的一个子领域,其主要区别在于使用深层的神经网络模型。深度学习模型通常包含多个隐层,可以学习更加复杂的特征表示,因此在某些任…
5次多项式轨迹规划(博途SCL源代码)
运动控制轨迹规划时,加速度不连续将会使电机抖动,产生机械冲击。凸轮表轨迹规划很多都是基于5次多项式轨迹规划。3次多项式轨迹规划请查看下面文章链接:
3次多项式轨迹规划(PLC SCL代码)_RXXW_Dor的博客-CSDN博客机器人、运动控制等常用的轨迹规划有三次多项式、五次多项式…
极限中的无穷小量和无穷大量
目录
极限中的无穷小量
无穷小量的比较
无穷小量的性质
无穷大量和无穷小量的关系 极限中的无穷小量 在高等数学数学分析中,无穷小量是一个以数0为极限的变量,即当自变量x无限接近于某个点(或绝对值无限增大)时,函…
朋友圈大佬都去读研了,这份备考书单我码住了
作者简介: 辭七七,目前大二,正在学习C/C,Java,Python等 作者主页: 七七的个人主页 文章收录专栏: 七七的闲谈 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖…
线性代数的本质(七)——特征值和特征向量
特征值和特征向量
本章特征值和特征向量的概念只在方阵的范畴内探讨。
相似矩阵 Grant:线性变换对应的矩阵依赖于所选择的基。 一般情况下,同一个线性变换在不同基下的矩阵不同。仍然以平面线性变换为例,Grant 选用标准坐标系下的基向量 i…
线性代数的本质笔记(3B1B课程)
文章目录 前言向量矩阵行列式线性方程非方阵点积叉积 前言
最近在复习线代,李永乐的基础课我刷了一下,感觉讲的不够透彻,和我当年学线代的感觉一样,就是不够形象。
比如,行列式为什么那么重要,它的含义究…
线性矩阵不等式(LMI)在控制理论中的应用
目录
(一)Matlab中的LMI处理工具包 (二)为什么LMI成为控制理论领域重要工具?
(三)LMI在与Lyapunov不等式的关系
(1)线性矩阵不等式 (2)线性矩阵…
线性代数的本质——几何角度理解
B站网课来自 3Blue1Brown的翻译版,看完醍醐灌顶,强烈推荐:
线性代数的本质
本课程从几何的角度翻译了线代中各种核心的概念及性质,对做题和练习效果有实质性的提高,下面博主来总结一下自己的理解 1.向量的本质
在物…
管理类联考——数学——汇总篇——知识点突破——代数——整式分式——记忆
文章目录 考点记忆/考点汇总——按大纲 整体目录大纲法记忆宫殿法绘图记忆法 局部数字编码法归类记忆法重点记忆法歌决记忆法谐音记忆法理解记忆法比较记忆法转图像记忆法可视化法 本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式…
线性代数 第一章 行列式
一、概念
不同行不同列元素乘积的代数和(共n!项)
二、性质 经转置行列式的值不变,即; 某行有公因数k,可把k提到行列式外。特别地,某行元素全为0,则行列式的值为0; 两行互换行列式…
线性代数 第二章 矩阵
一、概念
mxn个数排成的m行n列的表格
二、运算法则
三、初等变换
(1)用非零常数k乘矩阵的某一行(列);
(2)互换矩阵某两行(列)的位置;
(3&am…
高等数学应试考点速览(上)
极限
上界存在,则上确界存在数列极限 定义性质:唯一、有界(保序、夹逼、不等式性质)、保号、四则运算判定: 单侧:单调有界双侧:闭区间套增量:柯西审敛 归并和收敛子列聚点有限覆盖原…
机器人中的数值优化|【三】无约束优化,拟牛顿法,共轭梯度法理论与推导
机器人中的数值优化|【三】无约束优化,拟牛顿法,共轭梯度法理论与推导
拟牛顿法 Quasi-Newton Methods
为什么引入拟牛顿法
在前面的章节中,我们学习了牛顿法,牛顿法的核心是先通过将函数泰勒展开,近似为一个二阶项…
线性代数(七) 矩阵分析
前言
从性线变换我们得出,矩阵和函数是密不可分的。如何用函数的思维来分析矩阵。
矩阵的序列 通过这个定义我们就定义了矩阵序列的收敛性。 研究矩阵序列收敛性的常用方法,是用《常见向量范数和矩阵范数》来研究矩阵序列的极限。 长度是范数的一个特…
[02] Multi-sensor KIT: DSP 矩阵运算-加法,减法和逆矩阵,放缩,乘法和转置矩阵
1.概述
2.API
◄ arm_mat_init_f32 浮点矩阵初始化 ◄ arm_mat_add_f32 矩阵加法 ◄ arm_mat_mult_f32 矩阵乘法 ◄ arm_mat_inverse_f32 矩阵A的逆矩阵 ◄ arm_mat_scale_f32 矩阵A乘以系数 ◄ arm_mat_inverse_f32 矩阵A减法 ◄ arm_mat_inverse_f32 矩阵A的装置
3.矩阵初…
注意力机制是否比矩阵分解更好?——IS ATTENTION BETTER THAN MATRIX DECOMPOSITION?
原文链接:https://openreview.net/pdf?id1FvkSpWosOlhttps://openreview.net/pdf?id1FvkSpWosOl
代码库:GitHub - Gsunshine/Enjoy-Hamburger: [ICLR 2021 top 3%] Is Attention Better Than Matrix Decomposition?[ICL…
抖音seo源代码开源部署----基于开放平台SaaS服务
抖音SEO搜索是什么? 抖音SEO搜索是指在抖音平台上进行搜索引擎优化(Search Engine Optimization)的一种技术手段。 通过优化抖音账号、发布内容和关键词等,提高抖音视频在搜索结果中的排名,从而增加视频曝光量和用户点…
线性代数中涉及到的matlab命令-第一章:行列式
目录
1,逆序数
2,行列式定义和性质
2.1,常用特性及命令
2.2,求行列式
2.3,行列式的性质
2,行列式按行(列)展开
3,范德蒙德行列式 在学习线性代数过程中&#…
Euclid空间or欧式空间(定义、正交性、正交变换、对称变换)酉空间(定义、酉变换、Hermite变换、正规矩阵)
欧式空间的定义 例如: 再例如: 正交性 正交基与标准正交基 施密特正交化例题 正交变换与正交矩阵 对称变换与对称矩阵 正交变换与对称变换例题 酉空间介绍 …
【考研数学】矩阵三大关系的梳理和讨论 | 等价、相似、合同
文章目录 引言一、定义二、判别法写在最后 引言
昨天学了矩阵的合同关系,老汤讲义里也列举了三大关系的定义和判别法,方便我们进行区分。但是光看还是难以入脑,为此,我想自己梳理一遍,顺带也复习一下线代之前的所学。…
线性代数 --- 矩阵的QR分解,A=QR
矩阵的QR分解,格拉姆施密特过程的矩阵表示 首先先简单的回顾一下Gram-Schmidt正交化过程的核心思想,如何把一组线性无关的向量构造成一组标准正交向量,即,如何把矩阵A变成矩阵Q的过程。 给定一组线性无关的向量a,b,c,我…
短视频视频号矩阵系统源码独立部署开发对接
一、多账号矩阵管理功能(基于api接口开发与没有官方接口开发的区别) 基于API接口开发,可以通过调用官方提供的接口获取账号信息、创建新账号、更新账号设置等操作,实现自动化的账号管理绑定授权,通过相关的接口开发绑定…
【考研数学】线性代数第六章 —— 二次型(2,基本定理及二次型标准化方法)
文章目录 引言一、二次型的基本概念及其标准型1.2 基本定理1.3 二次型标准化方法1. 配方法2. 正交变换法 写在最后 引言
了解了关于二次型的基本概念以及梳理了矩阵三大关系后,我们继续往后学习二次型的内容。 一、二次型的基本概念及其标准型
1.2 基本定理
定理…
第 5 章 数组和广义表(稀疏矩阵的三元组顺序表存储实现)
1. 背景说明 为了节省存储空间,可以对这类矩阵进行压缩存储。所谓压缩存储是指:为多个值相同的元只分配一个存储空间,对零元不分配空间。 2. 示例代码
1)status.h
/* DataStructure 预定义常量和类型头文件 */
#include <string.h>#i…
基于共享矩阵的线性秘密共享方案原理、构造与代码实现
1 线性秘密共享方案 线性秘密共享方案是一种加密技术,用于将一个秘密信息分割成多个片段,并将这些片段分发给多个参与者,只有当足够数量的参与者合作时,才能还原出完整的秘密信息。 线性秘密共享方案的基本原理是使用多项式插…
名词解释----------命题、定理、推论、引理
1. 命题
在现代哲学、数学、逻辑学、语言学中,命题是指一个判断(陈述)的语句(实际表达的概念),这个概念是可以被定义并观察的现象。命题不是指判断(陈述)本身,而是指所表…
LA@二次型@标准化相关原理和方法
文章目录 标准化方法正交变换法🎈求矩阵的特征值求各特征值对应的线性无关特征向量组正交化各个向量组 配方法步骤例例 初等变换法原理总结初等变换法的步骤例 标准化方法
正交变换法🎈 二次型可标准化定理的证明过程给出使用二次型标准化的步骤 该方法…
【算法|前缀和系列No.5】leetcode1314. 矩阵区域和
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【Leetcode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…
牛客:NC59 矩阵的最小路径和
牛客:NC59 矩阵的最小路径和 文章目录 牛客:NC59 矩阵的最小路径和题目描述题解思路题解代码 题目描述 题解思路
动态规划,递推公式:matrix[i][j] min(matrix[i-1][j], matrix[i][j-1])
题解代码
func minPathSum( matrix [][…
【考研数学】线性代数第六章 —— 二次型(3,正定矩阵与正定二次型)
文章目录 一、基本概念1.1 引例1.2 正定二次型概念 二、正定二次型的判别写在最后 一、基本概念
1.1 引例
(1)二次型 f ( x 1 , x 2 , x 3 ) x 1 2 3 x 2 2 2 x 3 2 X T A X f(x_1,x_2,x_3)x_1^23x_2^22x_3^2\pmb{X^TAX} f(x1,x2,x3)x123…
2.1 向量与线性方程组
一、行图像与列图像
线性代数的中心问题是求解线性方程组。线性的意思是这些方程的未知数是一次的,即每个未知数只会乘数字,而不会出现 x x x 与 y y y 相乘的项。下面是一个由两个未知数组成的方程组: 两个方程 两个未知数 { x − 2 y 1…
06 MIT线性代数-列空间和零空间 Column space Nullspace
1. Vector space
Vector space requirements vw and c v are in the space, all combs c v d w are in the space
但是“子空间”和“子集”的概念有区别,所有元素都在原空间之内就可称之为子集,但是要满足对线性运算封闭的子集才能成为子空间
中 2 …
计算机图形学——二维变换
二维变换
概念
应用于对象几何描述并改变其位置、方向或者大小的变换叫做几何变换,有时候也被叫做建模变换。而本文仅讨论平面中的几何变换,即二维变换。
矩阵表示和齐次坐标
对于普通的2x2矩阵,我们总是要将平移项与其它变换对应的矩阵写…
【考研数学】数学“背诵”手册 | 需要记忆且容易遗忘的知识点
文章目录 引言一、高数常见泰勒展开 n n n 阶导数公式多元微分函数连续、可微、连续可偏导之间的关系多元函数极值无条件极值条件极值 三角函数的积分性质华里士公式( “点火”公式 )特殊性质 原函数与被积函数的奇偶性结论球坐标变换公式 二、写在最后 …
Chimera:混合的 RLWE-FHE 方案
参考文献:
[HS14] S. Halevi and V. Shoup. Algorithms in HElib. In Advances in Cryptology–CRYPTO 2014, pages 554–571. Springer, 2014.[HS15] S. Halevi and V. Shoup. Bootstrapping for HElib. In Advances in Cryptology–EUROCRYPT 2015, pages 641–6…
51.MongoDB聚合操作与索引使用详解
聚合操作
聚合操作允许用户处理多个文档并返回计算结果。
从效果而言,聚合框架相当于 SQL 查询中的GROUP BY、 LEFT OUTER JOIN 、 AS等。
聚合管道
整个聚合运算过程称为管道(Pipeline),由多个阶段(Stage…
2.预备知识-3GPT版
#pic_center R 1 R_1 R1 R 2 R^2 R2 目录 知识框架No.1 数据操作数据预处理一、N维数组样例二、创建数组三、访问元素四、数据操作D2L注意点五、数据预处理D2L注意点六、QA No.2 线性代数一、标量二、向量1、基本操作2、空间表示3、乘法 三、矩阵1、基本操作2、乘法3、空间表…
数组与链表算法-矩阵算法
目录 数组与链表算法-矩阵算法
矩阵相加
C代码
矩阵相乘
C代码
转置矩阵
C代码
稀疏矩阵
C代码 数组与链表算法-矩阵算法 矩阵相加
矩阵的相加运算较为简单,前提是相加的两个矩阵对应的行数与列数必须相等,而相加后矩阵的行数与列数也是相同的。…
【特殊矩阵的压缩存储】
文章目录 特殊矩阵的压缩存储特殊的矩阵 特殊矩阵的压缩存储
矩阵:一个由m x n个元素排成的m行n列的表。 矩阵的常规存储: 将矩阵描述为一个二维数组。 矩阵的常规存储的特点: 可以将元素进行随机存取; 矩阵运算非常简单…
安装 GMP、NTL、CTMalloc ,编译 OpenFHE
参考文献:
[ABB22] Al Badawi A, Bates J, Bergamaschi F, et al. Openfhe: Open-source fully homomorphic encryption library[C]//Proceedings of the 10th Workshop on Encrypted Computing & Applied Homomorphic Cryptography. 2022: 53-63.openfheorg/o…
ALS算法在菜品智能推荐系统的应用
核心推荐模块的推荐算法是基于用户推荐模 型(user_model)协同过滤的矩阵分解过滤算法 ALS。其算法原理可叙述为: ALS收集大数据样本的用户评分喜好信息,训 练推荐模型,基于该模型进行协同过滤。 对于任意一个形如用户-…
可达矩阵-邻接矩阵-以及有向图的python绘制
参考1 自定义输入矩阵来绘制
根据参考代码, 自定义 代码如下:
# 编程实现有向图连通性的判断
from pylab import mplmpl.rcParams[font.sans-serif] [SimHei]
mpl.rcParams[axes.unicode_minus] False
import numpy as np
import networkx as nx
imp…
08 MIT线性代数-求解Ax=b:可解性与结构Complete Solution of Ax=b
1. 可解的条件 Solvability conditions on b 检验Axb是否可解的方法是对增广矩阵进行行消元。如果矩阵A的行被完全消去的话,则对应的b的分量也要得0
两条关于b的限制条件(等价)
1. if a comb. of rows of A gives zero row, then same comb. of enties of b must …
一个特殊级数的敛散性判断
海涅定理
若函数 f ( x ) f(x) f(x)在 x 0 x_0 x0的去心领域 U ( x 0 , δ ) U(x_0,\delta) U(x0,δ)内有定义,则 lim x → x 0 f ( x ) A \lim_{x\rightarrow x_0}f(x)A limx→x0f(x)A的充要条件是:对任意以 x 0 x_0 x0为极限且包含于 U…
[100天算法】-有序矩阵中第K小的元素(day 58)
题目描述
给定一个 n x n 矩阵,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是排序后的第 k 小元素,而不是第 k 个不同的元素。示例:matrix [[ 1, 5, 9],[10, 11, 13],[12, 13, 15]
],
k …
06 MIT线性代数-线性无关,基和维数Independence, basis, and dimension
1. 线性无关 Independence
Suppose A is m by n with m<n (more unknowns than equations)
Then there are nonzero solutions to Ax0
Reason: there will be free variables! A中具有至少一个自由变量,那么Ax0一定具有非零解。A的列向量可以线性组合得到零向…
线性代数基础-行列式
一、行列式之前的概念
1.全排列: 把n个不同的元素排成一列,称为n个元素的全排列,简称排列 (实际上就是我们所说的排列组合,符号是A,arrange)
2.标准序列: 前一项均小于后一项的序列…
04-附注 三维空间中的线性变换
附注 三维空间中的线性变换 三维空间线性变换 这是关于3Blue1Brown
"线性代数的本质"的学习笔记。 三维空间线性变换 图1 绕y轴旋转90 绕y轴旋转90后,各基向量所在的坐标如图1所示。用旋转后的各基向量作为矩阵的列,就得到变换矩阵。变换矩阵…
08 叉积的标准介绍
叉积的标准介绍 基本概念几何解释 这是关于3Blue1Brown
"线性代数的本质"的学习笔记。 基本概念
向量 v ⃗ \vec{v} v 叉乘向量 w ⃗ \vec{w} w 的结果大小是这两个向量围成的平行四边形的面积,方向由右手定则确定。 v ⃗ w ⃗ \vec{v}\vec{w} v w - …
12 克莱姆法则的几何解释
克莱姆法则的几何解释 线性方程组求解正交变换克莱姆法则 这是关于3Blue1Brown
"线性代数的本质"的学习笔记。 线性方程组求解
克莱姆法则并非解线性方程组的最好方法(高斯消元法更好),了解它是为了加深对线性方程组的理解。 图…
VINS-Mono-后端优化 (一:预积分残差计算-IMU预积分约束)
这里先回顾一下预积分是怎么来的 VINS-Mono-IMU预积分 (三:为什么要预积分预积分推导) 这里贴出预积分的公式 具体含义解释看对对应的文章 整个误差函数如下 预积分 α \alpha α β \beta β γ \gamma γ 是用 IMU 预积分获得的增量&a…
线性代数-Python-04:线性系统+高斯消元的实现
文章目录 1 线性系统2 高斯-jordon消元法的实现2.1 Matrix2.2 Vector2.3 线性系统 3 行最简形式4 线性方程组的结构5 线性方程组-通用高斯消元的实现5.1 global5.2 Vector-引入is_zero5.3 LinearSystem5.4 main 1 线性系统 2 高斯-jordon消元法的实现
2.1 Matrix
from .Vecto…
矩阵的迹和矩阵的特征值的关系:tr(A)=Σλ(A)
矩阵的迹和矩阵的特征值的关系:tr(A)Σλ(A)
这篇博客将讨论矩阵的迹和矩阵的特征值的关系。
1、矩阵的迹
矩阵的迹(trace)通常定义为矩阵对角元的和。因此只有方阵才有迹。 t r ( A ) ∑ i 1 n a i i tr(A) \sum_{i1}^{n} a_{ii} tr(A)i1∑naii
2、矩阵…
用excel计算一个矩阵的转置矩阵
假设我们的原矩阵是一个3*3的矩阵:
125346789
现在求它的转置矩阵:
鼠标点到一个空白的地方,用来存放结果: 插入-》函数: 选择TRANSPOSE,这个就是求转置矩阵的函数: 点击“继续”:…
Unity3D 游戏编程中需要掌握的数学知识详解
前言
在Unity3D游戏编程中,数学知识是非常重要的。它涉及到游戏的物理模拟、碰撞检测、动画控制、图形渲染等方面。本文将详细介绍Unity3D游戏编程中需要掌握的数学知识,包括向量、矩阵、几何运算、三角函数等,并给出相应的技术详解和代码实…
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动? 旋转矩阵
点、向量和坐标系 三维空间由3个轴组成&…
matlab求矩阵的伪逆或者负二分之一次方
如果X不是满秩矩阵的时候,那么不能使用inv()函数来求X的逆,因为X此时不存在逆,但是我们可以求X的伪逆。
(1)有以下两种方法求X的伪逆: 假设 X[1 2 1;1 2 1;2 3 4]; 1, pinvXpinv(X); 2,
[U,D,P]svd(X);
r…
线性空间(也叫向量空间)、线性运算
线性空间、线性运算
线性空间,也称向量空间。
假设是一个非空集合,是一个实数域。
在中定义了一个加法:即对中任何两个元素和,总有中另外一个元素与它们相对应,称为和的和,记作: 在定义了一个…
1.2 向量的长度与点积
一、向量的点积
两个向量 v ( v 1 , v 2 ) \boldsymbol v(v_1,v_2) v(v1,v2) 与 w ( w 1 , w 2 ) \boldsymbol w(w_1,w_2) w(w1,w2)的点积或内积是数字 v ⋅ w \boldsymbol v\cdot\boldsymbol w v⋅w: v ⋅ w v 1 w 1 v 2 w 2 ( 1.2.1 ) \boldsymbo…
ROC曲线和PR曲线模板
import numpy as np # 导入NumPy库,用于科学计算
from sklearn.metrics import roc_curve, auc, precision_recall_curve # 从sklearn.metrics库导入roc_curve、auc和precision_recall_curve函数
import matplotlib.pyplot as plt # 导入matplotlib库中的pyplot模…
科学与工程计算基础(数值计算)知识点总结
数值计算 第1章 概论1.2 数值计算中的误差1.2.1 误差的来源和分类1.2.2 误差与有效数字1.2.3 数值运算的误差估计 1.3 误差定性分析和避免误差危害1.3.1 算法的数值稳定性1.3.3 避免误差危害 1.4 数值计算中算法设计的技术1.5 习题1.5.1 判断题1.5.2 计算题 第2章 插值法2.2 拉…
05 MIT线性代数-转置,置换,向量空间Transposes, permutations, spaces
1. Permutations P:
execute row exchanges
becomes PA LU for any invertible A
Permutations P identity matrix with reordered rows
mn (n-1) ... (3) (2) (1) counts recordings, counts all nxn permuations
对于nxn矩阵存在着n!个置换矩阵
,
2. Transpose: 2.…
【LeeCode】54.螺旋矩阵
给定一个二维数组 array,请返回「螺旋遍历」该数组的结果。
螺旋遍历:从左上角开始,按照 向右、向下、向左、向上 的顺序 依次 提取元素,然后再进入内部一层重复相同的步骤,直到提取完所有元素。
示例 1:…
积分表二(高等数学同济版中所有的积分公式)
文章目录 含有 x − a x a \sqrt{\pm \frac{x-a}{xa}} xax−a 或者 ( x − a ) ( b − x ) \sqrt{(x-a)(b-x)} (x−a)(b−x) 的积分含有三角函数函数的积分含有反三角函数的积分 (其中 a > 0 a>0 a>0)含有指数函数的积分含有对数函数的积分含有双曲函数的…
03 矩阵与线性变换
矩阵与线性变换 线性变换如何用数值描述线性变换特殊的线性变换反过来看总结 这是关于3Blue1Brown
"线性代数的本质"的学习笔记。 线性变换
如果一个变换具有以下两个性质,我们就称它是线性的:
一是直线在变换后仍然保持为直线二是原点必须…
【其他数学】结式 resultant
结式 resultant
2023年11月30日 #analysis 文章目录 结式 resultant介绍Sylvester矩阵应用在消元中的应用传递函数的化简 下链 介绍
结式用来计算曲线的交点、消元、找参数化曲线的隐含方程。 为了引出定义,思考如下问题: f ( x ) x 2 − 5 x 6 g (…
20231210 随机矩阵和M矩阵
1. 非负矩阵:矩阵元素均非负
定义 7.1.1 设 A ( a i j ) ∈ R m n \boldsymbol{A}\left(a_{i j}\right) \in \mathbb{R}^{m \times n} A(aij)∈Rmn, 如果 a i j ⩾ 0 , i 1 , ⋯ , m ; j 1 , ⋯ , n , a_{i j} \geqslant 0, \quad i1, \cdots, m ; j1, \cd…
【动手学深度学习】课程笔记 05-07 线性代数、矩阵计算和自动求导
05 线性代数
1. 基础知识补充
向量相关 矩阵相关 简单来说,范数是用来衡量矩阵(张量)大小的值,范数的值有不同的规定。 2. 代码实现
仅记录一些我比较陌生的知识。
张量的克隆
A torch.arange(20, dtypetorch.float32).resh…
MIT_线性代数笔记:第 15 讲 子空间投影
目录 投影(射影)Projections投影矩阵 Projections matrix为什么要投影 Why Project在高维投影 Projection in higher dimensions最小二乘 Least Squares 投影(射影)Projections
简单来说,两个向量之间的投影是将其中一…
MIT18.06线性代数 笔记3
文章目录 对称矩阵及正定性复数矩阵和快速傅里叶变换正定矩阵和最小值相似矩阵和若尔当形奇异值分解线性变换及对应矩阵基变换和图像压缩单元检测3复习左右逆和伪逆期末复习 对称矩阵及正定性
特征值是实数特征向量垂直>标准正交 谱定理,主轴定理
为什么对称矩…
webGL编程指南 第五章 MultiTexture.html
我会持续更新关于wegl的编程指南中的代码。
当前的代码不会使用书中的缩写,每一步都是会展开写。希望能给后来学习的一些帮助
git代码地址 :空 上一章节中我们学习texParameteri的使用,这一章节中我们两个图片进行混合
<!DOCTYPE html>
<htm…
克拉默法则,逆矩阵,体积
伴随矩阵 C C C是把矩阵所有元素都替换成代数余子式,然后再转置的矩阵
A的逆矩阵可以这么算 A − 1 1 d e t ( A ) C T A^{-1}\frac1{det(A)}C^T A−1det(A)1CT
证明: A C T AC^T ACT 的对角是A一行乘以这一行的余子式,根据行列式的计算方法,它的结果就是det(A),而非对角…
跟李沐学AI-深度学习课程05线性代数
线性代数
🏷sec_linear-algebra
在介绍完如何存储和操作数据后,接下来将简要地回顾一下部分基本线性代数内容。 这些内容有助于读者了解和实现本书中介绍的大多数模型。 本节将介绍线性代数中的基本数学对象、算术和运算,并用数学符号和相应…
【anaconda】numpy.dot 向量点乘小技巧
假设向量A[1,1], 向量B[2,3]。如果想知道他们的内积就可以输入如下代码: 当然,如果是两个列向量相乘,肯定是不对的 但是如果没有维度也一样可以求得内积,而且结果不会套在列表里
第二章矩阵 -矩阵及其运算(加减乘法)
目录: 一、矩阵的基本概念 1、行矩阵与列矩阵
2、零矩阵
3、负矩阵 4、方阵 1)、方阵的定义 2)、主对角线和次对角线
5、单位阵 6、只有一个数字的矩阵
7、同型矩阵 三、矩阵的运算 1、加法、减法
2、数乘运算 四、矩阵乘法
1、矩阵的乘…
【矩阵论】Chapter 2—内积空间知识点总结复习
文章目录 内积空间1 内积空间2 标准正交向量集3 Gram-Schmidt正交化方法4 正交子空间5 最小二乘问题6 正交矩阵和酉矩阵 内积空间
1 内积空间 内积空间定义 设 V V V是在数域 F F F上的向量空间,则 V V V到 F F F的一个代数运算记为 ( α , β ) (\alpha,\beta) (α…
C#用MathNet生成矩阵,并打印矩阵元素
文章目录 安装创建和显示矩阵 安装
MathNet.Numerics中提供了线性代数、微积分、特殊函数、概率论、随机函数、插值、最优化等一系列功能,是.net技术中首选的数值计算包。
其中,线性代数包LinearAlgebra包提供了向量、矩阵等数据结构,这些是…
6-3 求3*3整数矩阵对角线元素之和
#include<stdio.h>int main(){int a[3][3],sum0;int i ,j;printf("输入元素:\n");for(i0;i<3;i)for(j0;j<3;j)scanf("%d",&a[i][j]);for(i0;i<3;i)sumsuma[i][i];printf("总和为:%d",sum);return 0;}
54.螺旋矩阵(顺时针打印矩形元素)
题目
class Solution {public List<Integer> spiralOrder(int[][] matrix) {int m matrix.length, n matrix[0].length;int leftUpM 0, leftUpN 0, rightDownM m - 1, rightDownN n - 1;List<Integer> res new ArrayList<>();while (leftUpM < ri…
openGL 三:矩阵和向量
1.使用glm数学库进行矩阵和向量的计算 2.位置坐标可以看做一个向量 3.向量的移动,缩放,旋转,都是可以通过和矩阵的计算得出 4.向量的缩放乘一个44的矩阵 5.注意事项(有些版本的glm::mat4 不是默认构建一个单位44的矩阵)…
【矩阵论】Chapter 6—矩阵分解知识点总结复习(附Python实现)
文章目录 1 满秩分解(Full-Rank Factorization)2 三角分解(Triangular Factorization)3 正交三角分解(QR Factorization)4 奇异值分解(SVD) 1 满秩分解(Full-Rank Factor…
【重点】【矩阵】48. 旋转图像
题目 参考答案
法1:辅助矩阵
class Solution {public void rotate(int[][] matrix) {int n matrix.length;int[][] newMatrix new int[n][];for (int i 0;i < n; i) {newMatrix[i] matrix[i].clone();}for (int i 0; i < n; i) {for (int j 0; j <…
【视觉SLAM十四讲学习笔记】第四讲——李群与李代数基础
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵 【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角 【视觉SLAM十四讲学习笔记】第三讲——四元…
2.6 A 的 LU 分解
一、A LU
线性代数很多关键的概念实际上就是矩阵的分解(factorization)。原始矩阵 A A A 变成两个或三个特殊矩阵的乘积。第一个分解,实际上也是最重要的分解,来自消元法。因子 L L L 和 U U U 都是三角形矩阵,分…
线性代数基础【1】行列式
第一节 行列式的基本概念和性质
一、基本概念
①逆序
1,2和2,1是一对逆序
②逆序数
1,2,3,5,4的逆序数为1;1,3,2,5,4逆序数为4;
③行列式
④余子数和代数余子数
行列式挖掉一个数(例如aij),将原行列式去掉i行j列的行列式M,则M为余子数,代数余子数记为Aij,如果(ij)为偶数…
专注抖音短视频账号矩阵系统源头开发---saas工具
抖音账号|短视频矩阵分发系统 | 多账号管理发布 |MVC架 短视频矩阵分发系统是一种可以帮助企业、机构和个人高效分发短视频的工具。随着社交媒体的不断普及,短视频的使用越来越广泛,因此如何快速而准确地将短视频传播到不同的平台和账号上已经成为了一个…
PTA: 矩阵的乘法运算
矩阵的乘法运算 题目输入格式输出格式输入样例输出样例 代码 题目
线性代数中的矩阵可以表示为一个row*column的二维数组,当row和column均为1时,退化为一个数,当row为1时,为一个行向量,当column为1时&…
【矩阵论】Chapter 7—Hermite矩阵与正定矩阵知识点总结复习
文章目录 1 Hermite矩阵2 Hermite二次型3 Hermite正定(非负定矩阵)4 矩阵不等式 1 Hermite矩阵 定义 设 A A A为 n n n阶方阵,如果称 A A A为Hermite矩阵,则需满足 A H A A^HA AHA,其中 A H A^H AH表示 A A A的共轭转…
四元数,欧拉角,旋转矩阵,旋转向量
四元数,旋转矩阵,旋转向量,欧拉角
一、欧拉角
1、欧拉角是表达旋转的最简单的一种方式,形式上它是一个三维向量,其值分别代表物体绕坐标系三个轴(x,y,z轴)的旋转角度,默认旋转正向为逆坐标轴逆…
短视频矩阵软件哪个好用?
短视频频矩阵软件是一种可以帮助用户快速制作、发布和管理多个个短视频账号的工具,它可以让用户在不同的平台上展示自己的内容,提高品牌知名度和影响力,同时也可以节省时间和精力,提升效率和质量。。短视频频矩阵软件有很多种&…
格密码基础:垂直子空间与子格,q-ary垂直格
目录
一.写在前面
二.子空间垂直
2.1 理论解释
2.2 举例分析
三. 零空间
3.1 零空间与q-ary垂直格
3.2 零空间与行/列空间
四. 格密码相关 一.写在前面
格密码中的很多基础原语都来自于线性代数的基本概念,比如举几个例子:
格密码中的非满秩格…
短视频矩阵系统:赋予用户创造与分享的力量
在如今快节奏的社交网络时代,人们对于信息获取和娱乐方式的需求也逐渐发生了变化。作为当下最受欢迎的短视频平台之一,抖音短视频矩阵系统正以其独特的魅力和吸引力,深深地打动着亿万用户。
抖音短视频矩阵系统是一种基于移动端的短视频分享…
oj 1.8编程基础之多维数组 12:变幻的矩阵
描述
有一个N x N(N为奇数,且1 < N < 10)的矩阵,矩阵中的元素都是字符。这个矩阵可能会按照如下的几种变幻法则之一进行变幻(只会变幻一次)。 现在给出一个原始的矩阵,和一个变幻后的矩阵…
MATLAB中./和/,.*和*,.^和^的区别
MATLAB中./和/,.*和*,.^ 和^ 的区别 MATLAB中./和/,.*和*,.^ 和^ 的区别./ 和 / 的区别.//实验实验结果 .* 和 * 的区别.**实验实验结果 .^ 和^ 的区别.^n^n实验运行结果 MATLAB中./和/,.和,.^ 和^ 的区别 …
MIT线性代数笔记-第34讲-左右逆,伪逆
目录 34.左右逆,伪逆左右逆伪逆 打赏 34.左右逆,伪逆
左右逆
之前讲到的逆都是针对可逆方阵而言的,对于长方矩阵,实际上也有广义的逆,那就是左逆和右逆 左逆 当矩阵列满秩,即 r n r n rn时,…
MIT18.06线性代数 笔记1
文章目录 方程组的几何解释矩阵消元乘法和逆矩阵A的LU分解转置-置换-向量空间R列空间和零空间求解Ax0主变量 特解求解Axb可解性和解的结构线性相关性、基、维数四个基本子空间矩阵空间、秩1矩阵和小世界图图和网络复习一 方程组的几何解释
线性组合: 找到合适的x和…
线性代数运算方法总结
线性方程组的行列式解法(克拉默法则)
首先写出方程的系数行列式,第一列x1第二列x2以此类推,然后用每个方程式的结果分别代替第一列到第列,得到每个未知数对应的代数行列式,方程的解为代数行列式比系数行列…
【数值分析】LU分解解Ax=b,matlab自己编程实现
LU分解(直接三角分解,Doolittle分解) A x b , A L U Axb \,\,,\,\, ALU Axb,ALU { L y b U x y \begin{cases} Lyb \\ Uxy \end{cases} {LybUxy 矩阵 L {L} L 的对角元素为 1 {1} 1 ,矩阵 U {U} U 的第一行和 A {A} A …
MBA-数学题概念和公式
{}公差大于零的等差数列:多个数字组成的数列,两两之间差相等,且后值减前值大于0,如:{-2,0,2,4}为公差数列为2的等差数列.因数是指整数a除以整数b(b≠0) 的商正好是整数而没有余数,10的因数为 2和5圆柱体表面积 2πr 2πrh球体表名…
1125矩阵乘法(C语言)
一:题目 二:思路分析
1.对于学习过线性代数的人来说,对应公式十分熟悉,而对于没接触过线性代数的人来说,我们地一步要做的是从题目所给的公式中找规律 2.这个题目,给了我们三个变量n,m…
【线性代数】期末速通!
1. 行列式的性质
1.1 求一个行列式的值
特殊地,对角线左下全为0,结果为对角线乘积。行 r 列 c
1.2 性质
某行(列)加上或减去另一行(列)的几倍,行列式不变某行(列)乘 …
大连理工大学软件学院2022年秋季学期《矩阵与数值分析》上机作业
文章目录 《计算机科学计算》第二版162页第12题(1)162页第16题216页第12题 《数值分析方法与应用》一、基础知识部分1、5、 二、线性方程组求解2、6、 三、非线性方程组求解1、4、 四、插值与逼近1、5、7、 五、数值积分2、 六、微分方程数值解法1、 《计…
LeetCode74二分搜索优化:二维矩阵中的高效查找策略
题目描述
力扣地址
给你一个满足下述两条属性的 m x n 整数矩阵:
每行中的整数从左到右按非严格递增顺序排列。每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则&…
t2017030921字母矩阵
题1 字母矩阵(char)
【问题描述】 小Y才学C不久就写了一个字母矩阵的题,即给出一个数字N,画出一个最外围全是字母‘A’的中空矩形,当N5时形如下图:
AAAAA
A A
A A
A A
AAAAA 小Q看了这个图形后,想了想马上给出这样一个…
BM61 矩阵最长递增路径
题目 矩阵最长递增路径
给定一个 n 行 m 列矩阵 matrix ,矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径,使这条路径上的元素是递增的。并输出这条最长路径的长度。 这个路径必须满足以下条件: 1. 对于每个单元格,你…
MIT_线性代数笔记:第 18 讲 行列式及其性质
目录 行列式 Determinants性质 Properties 课程进入第二大部分,之前学习了大量长方形矩阵的性质,现在我们集中讨论方阵的性质,行列式和特征值将我们的又一个重点,求行列式则与特征值息息相关。 行列式 Determinants
行列式是一个…
【中等】54. 螺旋矩阵
题目
54. 螺旋矩阵 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]
示例 2: 输入&#…
【线性代数】两个向量组等价,其中一个向量组线性无关,另一个向量组也是线性无关吗?
一、问题
两个向量组等价,其中一个向量组线性无关,另一个向量组也是线性无关吗?
二、答案
不一定,当两个向量组中的向量个数也相同时,结论才成立.若向量个数不相同,结论不成立. 例如: 向量组一:(1,0),(0,1) 向量组二:(1,0),(0,1),(1,1) 两…
MIT_线性代数笔记:第 19 讲 行列式公式和代数余子式
目录 行列式公式 Formula for the determinant代数余子式 Cofactor formula 我们已经认识到了行列式的性质,应该推导出其公式了。 行列式公式 Formula for the determinant
行列式有如下三个性质:
det( I )1。如果交换行列式的两行,则行列式…
【最优化方法】无约束优化问题(最速下降法、牛顿法、最小二乘)
文章目录 最速下降法示例 牛顿法阻尼牛顿法示例 最小二乘问题 最速下降法
最速下降法(Steepest Descent Method)是一种基于负梯度方向进行迭代的最优化算法,用于寻找一个函数的最小值。该方法也被称为梯度下降法,是一种迭代的一阶…
短视频账号矩阵系统3年技术独立源头正规开发搭建
短视频账号矩阵3年技术独立开发打造是一个非常有挑战性和前景的项目。以下是一些建议,帮助你成功打造一个成功的短视频账号矩阵: 1. 确定目标受众:首先需要明确你的目标受众是谁,了解他们的兴趣爱好、年龄、性别等,以便…
向量投影:如何将一个向量投影到矩阵的行向量生成子空间?
向量投影:如何将一个向量投影到矩阵的行向量生成子空间?
前言
本问题是在学习Rosen梯度投影优化方法的时候遇到的问题,主要是对于正交投影矩阵(NT(NNT)-1N)的不理解,因此经过查阅资料,学习了关于向量投影的知识&…
【leetcode100-018】【矩阵】矩阵置零
【题干】
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
进阶:
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。一个简单的改进方案是使用 O(…
线性代数的本质——1 向量
向量是线性代数中最为基础的概念。
何为向量? 从物理上看, 向量就是既有大小又有方向的量,只要这两者一定,就可以在空间中随便移动。 从计算机应用的角度看,向量和列表很接近,可以用来描述某对象的几个不同…
线性代数的本质 1 向量
向量是线性代数中最为基础的概念。
何为向量? 从物理上看, 向量就是既有大小又有方向的量,只要这两者一定,就可以在空间中随便移动。 从计算机应用的角度看,向量和列表很接近,可以用来描述某对象的几个不同…
λ-矩阵的多项式展开
原文链接
定义. 对于 m n m \times n mn 的 λ \lambda λ-矩阵 A ( λ ) [ a 11 ( λ ) . . . a 1 n ( λ ) ⋮ ⋮ a m 1 ( λ ) . . . a m n ( λ ) ] \mathbf{A}(\lambda)\begin{bmatrix} a_{11}(\lambda) & ... & a_{1n}(\lambda)\\ \vdots & & \vdo…
【深度学习】S2 数学基础 P2 线性代数(下)
目录 范数的意义范数的数学意义范数之于深度学习的意义 L1 范数与 L2 范数L1 范数L2 范数 小结 本节博文是线性代数第二部分,主要内容为 L 1 L1 L1 范数与 L 2 L2 L2 范数;有关线性代数基础知识,请访问:【深度学习】S2 数学基础…
C#,数值计算,矩阵的行列式(Determinant)、伴随矩阵(Adjoint)与逆矩阵(Inverse)的算法与源代码
本文发布矩阵(Matrix)的一些初级算法。 一、矩阵的行列式(Determinant)
矩阵行列式是指矩阵的全部元素构成的行列式,设A(a)是数域P上的一个n阶矩阵,则所有A(a)中的元素组成的行列式称为矩阵A的行列式&…
基于CU,PO,RD,IPO矩阵图分析数据资产-自创
术语 数据资产:数据资产是具有价值的数据资源。没有价值的数据资源,通过采集,整理,汇总等加工后,也可以成为具有直接或间接价值的数据资产。传统企业逐渐数字化转型,尤其是互联网企业,都十分重视…
线性代数笔记2--矩阵消元
0. 简介
矩阵消元
1. 消元过程
实例方程组 { x 2 y z 2 3 x 8 y z 12 4 y z 2 \begin{cases} x2yz2\\ 3x8yz12\\ 4yz2 \end{cases} ⎩ ⎨ ⎧x2yz23x8yz124yz2 矩阵化 A [ 1 2 1 3 8 1 0 4 1 ] X [ x y z ] A \begin{bmatrix} 1 & 2 & 1 \\ 3 & …
插值(一)——多项式插值(C++)
插值
插值的作用是可以将原本比较难计算的函数转换为误差在一定范围内的多项式,比如在单片机中直接计算 x 、 log 2 x \sqrt{x}、\log_2x x 、log2x之类的函数是比较麻烦的,但是使用插值的方法就可以将其转换为误差可控的只有乘法和加减法的多项…
线性代数第一课+第二课总结
第一课
第一课是简单的行列式计算,主要就是要把左下角的数字全部转换为0,通过减去其他行的式子即可实现,最后把对角线的所有数字相乘,得到的结果是最后行列式的答案
第二课
例题1
硬算理论上其实也是可行的,但是使…
线性代数笔记3 1.1
学习视频: 2.2 矩阵运算(二)_哔哩哔哩_bilibili 包括内容:
p10矩阵运算(二)
p11特殊矩阵
p12逆矩阵(一)
p13逆矩阵(二)
计算机视觉基础:【矩阵】矩阵选取子集
OpenCV的基础是处理图像,而图像的基础是矩阵。 因此,如何使用好矩阵是非常关键的。 下面我们通过一个具体的实例来展示如何通过Python和OpenCV对矩阵进行操作,从而更好地实现对图像的处理。
示例
示例:选取矩阵中指定的行和列的…
(done) Positive Semidefinite Matrices 什么是半正定矩阵?如何证明一个矩阵是半正定矩阵? 可以使用特征值
参考视频:https://www.bilibili.com/video/BV1Vg41197ew/?vd_source7a1a0bc74158c6993c7355c5490fc600
参考资料(半正定矩阵的定义):https://baike.baidu.com/item/%E5%8D%8A%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/2152711?frge_ala 看看半正定矩阵的…
什么是正定矩阵?Positive Definite Matrices (done)
正定矩阵的定义:https://baike.baidu.com/item/%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/11030459
正定矩阵的作用、验证视频:https://www.bilibili.com/video/BV1Ag411M76G/?spm_id_from333.337.search-card.all.click&vd_source7a1a0bc74158c6993c…
由麦克斯韦方程组推出均匀平面电磁波及其特征
由麦克斯韦方程组推出均匀平面电磁波及其特征
均匀平面电磁波是指在传输方向垂直与传输方向垂直的平面上,电磁波的每一点的电场和磁场都相同,这种电磁波被称作均匀平面电磁波。
研究任何一种物理现象,当一种物理现象特别复杂的时候…
什么是短视频矩阵系统?效果是怎么样的?
短视频矩阵系统是一种通过将多个短视频连接起来形成一个整体的系统。它的效果是可以提供一种连贯而有序的观看体验,使观众可以连续地观看一系列相关的短视频内容。
短视频矩阵系统的运作方式如下:首先,用户在平台上选择一个短视频开始观看。…
抖去推账号矩阵+无人直播+文案引流系统开发搭建--开源
核心技术
1. AI自动直播:
智能系统通过丰富可定制的文案库, 拥有有料有趣的灵魂。不仅能自动语音讲解内容,还可以在直播中和用户灵活互动。直播中可将团购商品同话术自动上下架。 2. AI剪辑
可一键智能批量成片,也可跟着模板剪…
MIT_线性代数笔记:第 25 讲 对称矩阵和正定性
目录 对称矩阵 Symmetric matrices实特征值 Real eigenvalues正定矩阵 Positive definite matrices 对称矩阵是最重要的矩阵之一,其特征值为实数并且拥有一套正交特征向量。正定矩阵的性质则更好。 对称矩阵 Symmetric matrices
包含特殊性质的矩阵,例如…
线性代数基础【3】向量
第一节 向量的概念与运算
一、基本概念
①向量
②向量的模(长度)
③向量的单位化
④向量的三则运算
⑤向量的内积
二、向量运算的性质
(一)向量三则运算的性质
α β β αα (β γ) (α β) γk (α β) kα kβ(k l) α kα lα
(二)向量内积运…
线性代数:矩阵的定义
目录
一、定义
二、方阵
三、对角阵
四、单位阵
五、数量阵
六、行(列)矩阵 七、同型矩阵
八、矩阵相等
九、零矩阵
十、方阵的行列式 一、定义 二、方阵 三、对角阵 四、单位阵 五、数量阵 六、行(列)矩阵 七、同型矩…
编程语言MoonBit新增矩阵函数的语法糖
MoonBit更新
1. 新增矩阵函数的语法糖
新增矩阵函数的语法糖,用于方便地定义局部函数和具有模式匹配的匿名函数:
fn init {fn boolean_or { // 带有模式匹配的局部函数true, _ > true_, true > true_, _ > false}fn apply(f, x) {f(x)}le…
牛客周赛 Round 20 解题报告 | 珂学家 | 状压DP/矩阵幂优化 + 前缀和的前缀和
前言 整体评价
这场比赛很特别,是牛客周赛的第20场,后两题难度直线飙升了。
前四题相对简单,E题是道状压题,历来状压题都难,F题压轴难题了,感觉学到了不少。 A. 赝品
先求的最大值
然后统计非最大值的个…
机械臂雅可比矩阵的矢量积理解和matlab实现
雅可比矩阵的第Ji列:
关于一些基本概念可以参考博客,部分细节如下:
每个移动关节,Ji可以这样计算: 每个旋转关节,Ji这样计算: 有时候要求按照末端执行器坐标系{n}来执行一些位移旋转之类的…
【算法小记】——机器学习中的概率论和线性代数,附线性回归matlab例程
内容包含笔者个人理解,如果错误欢迎评论私信告诉我 线性回归matlab部分参考了up主DR_CAN博士的课程 机器学习与概率论
在回归拟合数据时,根据拟合对象,可以把分类问题视为一种简答的逻辑回归。在逻辑回归中算法不去拟合一段数据而是判断输入…
整理了一下常用的LaTeX数学公式语法,未完待续
为了方便对应,后面会拆一下
公式代码放入LaTeX编译环境中时,两边需要加入$$:
$$公式代码$$ 1,分解示例
L^{A}T_{E}X\,2_{\epsilon} c^{2}a^{2}b^{2} \tau\phi \cos2\pi1 f\, \,a^{x}\,\,b \heartsuit \cos^{2}\theta \sin^{2}\theta 1.0…
5_机械臂运动学基础_矩阵
上次说的向量空间是为矩阵服务的。 1、学科回顾 从科技实践中来的数学问题无非分为两类:一类是线性问题,一类是非线性问题。线性问题是研究最久、理论最完善的;而非线性问题则可以在一定基础上转化为线性问题求解。 线性变换: 数域…
矩阵理论及其应用邱启荣习题3.5题解
(1) P ( − 1 0 1 − 1 − 1 2 1 1 − 1 ) \begin{pmatrix} -1 & 0&1 \\ -1 & -1&2\\1&1&-1 \end{pmatrix} −1−110−1112−1 A ( 1 0 1 1 1 0 − 1 2 1 ) \begin{pmatrix} 1 & 0&1 \\ 1 & 1&0\\-1&2&1 \end{pmat…
【线性代数与矩阵论】矩阵的酉相似
矩阵的酉相似(合同变换)
2023年11月7日 #algebra 文章目录 矩阵的酉相似(合同变换)1. 酉矩阵2. 酉相似3. Schur分解定理4. 正规矩阵5. 酉相似对角化6. Hermit矩阵,反Hermit矩阵及酉矩阵的特性7. Hermit矩阵的正定性下…
线性代数----------学习记录
线性代数发展历程
(1)线性方程组:例如二元一次方程组;
(2)行列式:determinant,克莱默,莱布尼兹;
(3)矩阵:方程个数与未知数的个数可…
理顺 QR 分解算法
咱们网站的这个公式编辑器,估计是后台生成图片后贴回来的,固定分辨率而且分辨率不高。 还不如先离线 latex 生成 pdf 后再截图上来 1. Why QR
When A and b are known, to solver the minimization of , where .
The reduction of A to various canoni…
线性代数--------学习总结
高斯消去法:对于任意的矩阵,总是能够利用倍加和行变换的方法变化成为阶梯形矩阵(每一行第一个非零元叫做主元,他所在的列就叫做主列------每一行的主列都在他上方任意一行主列的右边)和行简化阶梯矩阵(主元…
线性代数------矩阵的运算和逆矩阵
矩阵VS行列式
矩阵是一个数表,而行列式是一个具体的数;
矩阵是使用大写字母表示,行列式是使用类似绝对值的两个竖杠;
矩阵的行数可以不等于列数,但是行列式的行数等于列数;
1.矩阵的数乘就是矩阵的每个…
深度学习与神经网络pytorch版 2.3 线性代数
深度学习与神经网络pytorch版 2.3 线性代数
目录
深度学习与神经网络pytorch版 2.3 线性代数
1. 简介
2. 线性代数
2.3.1 标量
编辑2.3.2 向量
2.3.3 矩阵
2.3.4 张量及其性质
2.3.5 降维
2.3.6 非降维求和
2.3.7 点积
2.3.8 矩阵-向量积
2.3.9 矩阵-矩阵乘法
…
线性代数:矩阵的初等变换
目录
一、初等行变换
行阶梯 / 行最简
性质 二、矩阵的标准型 三、矩阵的等价
四、初等矩阵 五、重要性质与定理 一、初等行变换
行阶梯 / 行最简 性质 二、矩阵的标准型 三、矩阵的等价 四、初等矩阵 五、重要性质与定理
Nicn的刷题日常之杨氏矩阵(三种方法求解,逐级递增详解,手把手教学,建议三连收藏)
目录
1.杨氏矩阵知识普及:什么是样式矩阵
2.题目描述
3.解题
3.1暴力求解,遍历法
3.2巧妙解题:对角元素法
3.3将巧解法封装为函数
4.结语 1.杨氏矩阵知识普及:什么是样式矩阵 杨氏矩阵,是对组合表示理论和…
MIT_线性代数笔记:第 32 讲 复习三
目录 主要内容例题:1)微分方程:2)一个 3x3 矩阵 A 具有特征值 λ 1 0 , λ 2 c , λ 3 2 λ_10,λ_2c,λ_32 λ10,λ2c,λ32。对应的特征向量为 x …
数据结构|对称矩阵压缩存储的下标公式推导|如何求对称矩阵压缩存储对应的一维数组下标
因为考试的时候可能会给很多情况的变式题,所以要会推导而不是背公式,情况变了,公式就不管用了。 行优先、只存储主对角线下三角区: 矩阵下标 ai,j(i>j)->一维数组下标 B[k] 按照行优先的原则,确定 ai,j 是一维数…
机器人运动学林沛群——变换矩阵
对于仅有移动,由上图可知: A P B P A P B o r g ^AP^BP^AP_{B org} APBPAPBorg
对于仅有转动,可得: A P B A R B P ^AP^A_BR^BP APBARBP 将转动与移动混合后,可得: 一个例子 在向量中ÿ…
线代:认识行列式、矩阵和向量
本文主要参考的视频教程如下: 8小时学完线代【中国大学MOOC*小元老师】线性代数速学_哔哩哔哩_bilibili 另外这个视频可以作为补充: 【考研数学 线性代数 基础课】—全集_哔哩哔哩_bilibili 行列式的概念和定义 一般会由方程组来引出行列式 比如一个二阶…
灰度共生矩阵各参数说明
灰度共生矩阵的特征: 角二阶矩(Angular Second Moment, ASM) ASMsum(p(i,j).^2) p(i,j)指归一后的灰度共生矩阵 角二阶矩是图像灰度分布均匀程度和纹理粗细的一个度量,当图像纹理绞细致、灰度分布均匀时,能量值较大,…
线性代数基础【4】线性方程组
第四章 线性方程组
一、线性方程组的基本概念与表达形式 二、线性方程组解的基本定理
定理1 设A为mXn矩阵,则
(1)齐次线性方程组AX0 只有零解的充分必要条件是r(A)n;
(2)齐次线性方程组AX0 有非零解(或有无数个解)的充分必要条件是r(A)<n
推论1 设A为n阶矩阵,则…
Scipy 高级教程——稀疏矩阵
Python Scipy 高级教程:稀疏矩阵
Scipy 提供了处理稀疏矩阵的工具,这对于处理大规模数据集中的稀疏数据是非常有效的。本篇博客将深入介绍 Scipy 中的稀疏矩阵功能,并通过实例演示如何应用这些工具。
1. 稀疏矩阵的表示
在 Scipy 中&#…
MIT_线性代数笔记:复习二
目录 第二单元主要内容例题 第二单元主要内容
正交矩阵 Q,用矩阵形式描述正交性质。
投影矩阵 P,最小二乘法,在方程无解时求“最优解”。 Gram-Schmidt 正交化——从任意一组基得到标准正交基,策略是从向量 中减去投影到其它向…
MIT_线性代数笔记:第 26 讲 复矩阵;快速傅里叶变换
目录 复向量 Complex vectors复矩阵 Complex matrices傅里叶变换 Fourier transform快速傅里叶变换 Fast Fourier transform 实矩阵也可能有复特征值,因此无法避免在矩阵运算中碰到复数,本讲学习处理复数矩阵和复向量。 最重要的复矩阵是傅里叶矩阵&…
第22章 补充一下实变函数的势,测度,退化矩阵,对称矩阵
之前讲到微分,再深入的话就不够了,补充一下实变函数的知识。
集这个概念可以说很重要,但又不那么重要,具有某种特性的汇集,这个要一直牢记。比如说有理数,无理数,比如方程的解,它都…
【现代控制系统】最小实现与互质分式
最小实现和互质分式
2023年12月12日 文章目录 最小实现和互质分式1. 实现问题2. SISO严格正则系统的实现2.1 能控标准1型实现2.2 能观标准2型实现2.3 能观标准1型实现2.4 能控标准2型实现2.5 最小实现2.6 完全表征 3. 计算互质分式3.1 使用西尔韦斯特结式 4. SISO基于Markov参…
线性代数逆矩阵的求法
在线性代数中,逆矩阵是一个非常重要且有趣的概念。一个 n 阶方阵 A 的逆矩阵,记作 A^-1,是指存在另一个 n 阶方阵 B,使得 A 和 B 的乘积等于单位矩阵 E,即: A * B E 或者等价地: B * A E 这里…
线性代数:线性方程组解的结构
目录
齐次/非齐次方程组的解
Ax 0 的解的性质
定理
Ax b 的解的性质
相关证明
例1
例2
例3 齐次/非齐次方程组的解 Ax 0 的解的性质 定理 Ax b 的解的性质 相关证明 例1 例2 例3
TensorFlow2.x 精选笔记(1)数据基本操作与线性代数
学习参考:
动手学深度学习2.0Deep-Learning-with-TensorFlow-bookpytorchlightning
一、数组与张量
虽然张量看起来是复杂的对象,但它们可以理解为向量和矩阵的集合。理解向量和矩阵对于理解张量至关重要。
向量是元素的一维列表,向量是一…
线性代数:向量、张量、矩阵和标量
线性代数:向量、张量、矩阵和标量
背景
在线性代数中,向量、张量、矩阵和标量都属于基础概念,特别是最近AI的爆火,向量和张量的概念也越来越普及,本文将介绍下这些基本概念。
1. 标量(Scalar࿰…
十二、线性代数二-二次型:
目录
1、二次型的定义:
2、二次矩阵与二次型的理解:
3、二次型矩阵的性质:
4、二次型的标准型:
5、二次型的正定型:
①正定型的概念:
②二次型正定型的判定:
SMIC思洣客矩阵:重塑数字经济的未来
经济的发展
经济是供需满足的过程,它涵盖了社会物资的生产和再生产过程。在这个过程中,经济活动遵循着生产和再生产的规律,通过生产、分配、交换和消费的过程,不断地形成和再造价值。从传统的市场经济到现代的智能经济࿰…
MATLAB中的稀疏矩阵和密集矩阵
在MATLAB中,矩阵可以表示为密集或稀疏格式。通常,矩阵默认以密集格式存储,这意味着每个元素都明确地存储在内存中,无论它的值是多少。然而,当矩阵含有大量的零元素时,这种存储方式就会变得非常低效。为了更…
十、线性代数二-线性相关
目录
1、线性相关的概念:
2、线性相关的代数表示:
3、线性相关的判断方法: 理解:线性相关指的是 向量组(α1,α2,α3,...)的 秩是 小于 k 的元数的,即齐次…
【01】深度学习——数学基础 | 线性代数 | 微积分 |概率
深度学习 1.线性代数1.1标量(scalar)1.2向量(Vector)1.2.1模长和范数1.2.2单位向量1.2.3向量的内积1.2.4向量的外积 1.3矩阵(Matrix)1.3.1矩阵转置1.3.2矩阵乘法1.3.3矩阵乘法的性质 1.4张量(Tensor) 2.微积分2.1极限2.2导数2.2.1导数和极限2.2.2导数和极…
MIT_线性代数笔记:线性代数常用概念及术语总结
目录 1.系数矩阵2.高斯消元法3.置换矩阵 Permutation4.逆矩阵 Inverse5.高斯-若尔当消元法6.矩阵的 LU 分解7.三角矩阵 1.系数矩阵
线性代数的基本问题就是解 n 元一次方程组。例如:二元一次方程组 2 x − y 0 − x 2 y 3 \begin{align*} & 2x - y 0\\ &am…
标量、向量、矩阵和张量的区别?
标量、向量、矩阵和张量是数学和物理学中常用的概念,它们在多维数据表示和处理中扮演着关键角色。下面是这些概念的基本区别:
标量(Scalar):
-标量是单个数字,用于表示单一的量。 -它没有方向。 -在数学中࿰…
c# 线性代数 克·施密特(Gram Schmidt)
Gram-Schmidt 方法是一种用于将线性无关的向量集合转化为一组正交(垂直)的向量集合的数学技术。这个方法是在线性代数中常用的一种技术,用于处理向量空间中的正交化和标准化操作。Gram-Schmidt 方法的主要思想是,通过一系列的投影…
使用Eigen3计算旋转平移缩放矩阵
一、fromPositionOrientationScale的使用方法 二、computeScalingRotation的使用方法
三、参考资料
eigen - What is the difference between computeScalingRotation and computeRotationScaling - Stack Overflow
线性代数的几何意义简单总结
矩阵的意义
矩阵既可以理解为一组(列)基向量,也可以理解为线性变换。
某个向量左乘矩阵表示向量在用新的基向量表示对应在原始坐标系下的坐标,也可以视为经过线性变换后的坐标。
原始基向量都是单位矩阵,其他矩阵都…
(done) 什么是正定矩阵?Positive Definite Matrices
正定矩阵的定义:https://baike.baidu.com/item/%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/11030459
正定矩阵的作用、验证视频:https://www.bilibili.com/video/BV1Ag411M76G/?spm_id_from333.337.search-card.all.click&vd_source7a1a0bc74158c6993c…
C#,数值计算,矩阵的乔莱斯基分解(Cholesky decomposition)算法与源代码
一、安德烈路易斯乔尔斯基
安德烈路易斯乔尔斯基出生于法国波尔多以北的查伦特斯海域的蒙古扬。他在波尔多参加了Lyce e,并于1892年11月14日获得学士学位的第一部分,于1893年7月24日获得第二部分。1895年10月15日,乔尔斯基进入莱科尔理工学院…
算法| 977.有序数组的平方 209.长度最小的子数组 59.螺旋矩阵II
977.有序数组的平方 简单题
/*** param {number[]} nums* return {number[]}*/
var sortedSquares function(nums) {const arr []for(let i 0; i < nums.length;i){arr[i] nums[i]*nums[i]}return arr.sort((a,b)> a-b)
};209.长度最小的子数组
考察: 不…
(done) 什么是特征值和特征向量?如何求特征值的特征向量 ?如何判断一个矩阵能否相似对角化?
什么是齐次方程? https://blog.csdn.net/shimly123456/article/details/136198159
行列式和是否有解的关系? https://blog.csdn.net/shimly123456/article/details/136198215
特征值和特征向量 参考视频:https://www.bilibili.com/video/BV…
(done) 矩阵的对角化,以及是否可对角化的判断、还有对角化的本质。相似对角化计算过程
相似对角化 和 对角化 很大程度上是一回事 甚至判断两个矩阵的相似性,也跟对角化有很大关系
参考视频1:https://www.bilibili.com/video/BV1PA411T7b5/?spm_id_from333.788&vd_source7a1a0bc74158c6993c7355c5490fc600
参考视频2:http…
十一、线性代数二-矩阵的对角化:
目录
①矩阵对角化的概念:
编辑
② 矩阵对角化的特点:
③判断方阵是否可以对角化步骤: ①矩阵对角化的概念: ② 矩阵对角化的特点: 1、P 是由 方阵 A 的所有 特征向量 以列 的形式 组成的。 2、得到的对角矩阵是…
深入浅出:探究过完备字典矩阵
在数学和信号处理的世界里,我们总是在寻找表达数据的最佳方式。在这篇博文中,我们将探讨一种特殊的矩阵——过完备字典矩阵,这是线性代数和信号处理中一个非常有趣且实用的概念。
什么是过完备字典矩阵?
首先,我们先…
采用遗传算法搜索MAC效率最高的矩阵乘规模
如何采用遗传算法搜索MAC效率最高的矩阵乘规模 具体实现MAC效率评估代码(eval.py)遗传算法实现 本文介绍了采用遗传算法搜索MAC效率最高的矩阵乘规模 需求背景: 一些AI加速卡在做矩阵乘时,因硬件或软件的约束,并不是规模越大MAC效率越高在测试AI加卡的实际算力时,采用MAC效率最…
机器学习——线性代数中矩阵和向量的基本介绍
矩阵和向量的基本概念
矩阵的基本概念(这里不多说,应该都知道) 而向量就是一个特殊的矩阵,即向量只有一列,是个n*1的矩阵 注:一般矩阵用大写字母表示,向量用小写字母表示
矩阵的加减运算 两个…
信息矩阵、hessian矩阵与协方差矩阵
文章目录 协方差矩阵联合概率密度hessian矩阵marginalize 本节探讨信息矩阵、hessian矩阵与协方差矩阵的关系,阐明边缘化的原理。 一个简单的示例,如下: 来自 David Mackay. “The humble Gaussian distribution”. In: (2006). 以及手写vio第…
深度学习 精选笔记(1)数据基本操作与线性代数
学习参考:
动手学深度学习2.0Deep-Learning-with-TensorFlow-bookpytorchlightning
①如有冒犯、请联系侵删。 ②已写完的笔记文章会不定时一直修订修改(删、改、增),以达到集多方教程的精华于一文的目的。 ③非常推荐上面(学习参考&#x…
窥探向量乘矩阵的存内计算原理—基于向量乘矩阵的存内计算
在当今计算领域中,存内计算技术凭借其出色的向量乘矩阵操作效能引起了广泛关注。本文将深入研究基于向量乘矩阵的存内计算原理,并探讨几个引人注目的代表性工作,如DPE、ISAAC、PRIME等,它们在神经网络和图计算应用中表现出色&…
刷题第2天(中等题):LeetCode59--螺旋矩阵--考察模拟能力(边界条件处理)
LeetCode59:
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1: 输入:n 3
输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2:
输入:…
Eigen-矩阵切片和索引
矩阵切片和索引 一、概述二、基本的切片三、编译时间大小和增量四、相反的顺序五、索引数组六、自定义索引列表 一、概述
本页介绍了操作符 () 为索引子集行和列提供的多种可能性。这个API已经在特性3.4中引入。它支持块API提出的所有特性,以及更多。特别是&#x…
Tiktok矩阵系统搭建的逻辑和源代码!
很多和我一样从事外贸工具开发的朋友都清楚,TikTok矩阵系统不仅确保了平台的高效运行,还为用户提供了个性化的内容推荐,从而大大提升了用户黏性,因此很多人都乐意去开发类似的工具,下面我们就来说说Tiktok矩阵系统搭建…
P9905 [COCI 2023/2024 #1] AN2DL 【矩阵区间最大值】
文章目录 题目大意1.输入格式2.输出格式3.数据范围与约定 思路维护每一行区间维护每一列区间维护区间最大值code↓ 完结撒花( ̄▽ ̄) / 题目大意
给定 n , m , r , s n,m,r,s n,m,r,s 和一个 n m n\times m nm 的整数矩阵 A A A,求它每个 …
Python线性代数傅里叶分析和动态系统模拟分析之一
要点
Python向量数值计算、可视化,线性独立性和子空间。了解欧几里德距离、余弦相似度和皮尔逊相关性应用案例:Python数值计算文档相似度时间序列和特征检测示例:Python信号处理边缘检测器, K均值示例:随机簇质心分布Python傅里叶…
LeetCode240题:搜索二维矩阵II(python3)
代码思路: “根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素,以 matrix 中的左下角元素为标志数 flag ,则有: 若 flag > target ,则 target 一定在 flag 所在行的上方 ,即 flag 所在行可被消去,…
有趣的数学 矩阵的秩描述了什么信息?
一、什么是矩阵的秩? 矩阵的秩是线性代数领域中一个非常重要的概念,因为它帮助我们知道是否可以找到方程组的解。矩阵的秩还可以帮助我们了解其向量空间的维数。 矩阵的秩是最高阶非零次数的阶数。矩阵的秩等于其中线性独立的行(或列…
25高数考研张宇 -- 公式总结(更新中)
1. 两个重要极限
(1) lim x → 0 sin x x 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}1 limx→0xsinx1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}1 limf(x)→0f(x)sinf(x)1. (2) lim …
矩阵爆破逆向-条件断点的妙用
不知道你是否使用过IDA的条件断点呢?在IDA进阶使用中,它的很多功能都有大作用,比如:ida-trace来跟踪调用流程。同时IDA的断点功能也十分强大,配合IDA-python的输出语句能够大杀特杀!
那么本文就介绍一下这…
【基础知识】协方差矩阵/协方差
协方差矩阵
协方差矩阵是一个描述多维随机变量线性相关性的矩阵。它是由各个随机变量的协方差组成的矩阵。在统计学和概率论中,协方差是用来衡量两个随机变量在它们的均值变化时是如何一起变化的。
对于一组随机变量 X ( X 1 , X 2 , . . . , X n ) X (X_1, X_…
机器人 标准DH与改进DH
文章目录 1 建立机器人坐标系1.1 连杆编号1.2 关节编号1.3 坐标系方向2 标准DH(STD)2.1 确定X轴方向2.2 建模步骤2.3 变换顺序2.4 变换矩阵3 改进DH(MDH)3.1 确定X轴方向3.2 建模步骤3.3 变换顺序3.4 变换矩阵4 标准DH与改进DH区别5 Matlab示例参考链接1 建立机器人坐标系
1.1…
「优选算法刷题」:最长回文子串
一、题目
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。 示例 1:
输入:s "babad"
输出:"bab"
解释:"aba"…
Matplotlib数据可视化实战-2绘制折线图(2)
2.11营业额可视化
已知某学校附近一个烧烤店2022年每个月的营业额如下图所示。编写程序绘制折线图对该烧烤店全年营业额进行可视化,使用红色点画线连接每个月的数据,并在每个月的数据处使用三角形进行标记。 烧烤店营业额 月份123456789101112营业额/万…
【计算机图形学】 线性代数在图形学中的应用
目录 0 引言1 线性代数应用1.1 点乘1.2 叉乘1.3 矩阵 🙋♂️ 作者:海码007📜 专栏:计算机图形学专栏💥 标题:【计算机图形学】 线性代数在图形学中的应用❣️ 寄语:对知识永远有兴趣ÿ…
0101二阶与三阶行列式-行列式-线性代数
一 引例
求解二元一次方程组 { a 11 x 1 a 12 x 2 b 1 a 21 x 1 a 22 x 2 b 2 \begin{cases} a_{11}x_1a_{12}x_2b_1\\ a_{21}x_1a_{22}x_2b_2\\ \end{cases} {a11x1a12x2b1a21x1a22x2b2 解: 1 a 21 − 2 a 11 ⇒ x 2 a 11 b 2 − a…
运筹学_1.1.4 线性规划问题-解的概念
1.1.4 线性规划问题-解的概念 一、可行解与最优解二、基的概念三、基变量、基向量;非基变量、非基向量;基解、基可行解;四、最优解与可行解、基可行解的关系五、用例题(枚举法)巩固基解、基可行解、最优解三个概念1、例…
Armadillo:矩阵类、向量类、Cube类和泛型类
文章目录 矩阵类、向量类、Cube类和泛型类Mat<type>matcx_matCol<type>veccx_vecRow<type>rowveccx_rowvecCube<type>cubecx_cubefield<object_type>SpMat<type>
Armadillo:C++线性代数运行库的版本更迭史
API 添加和更改的历史记录 文章目录 API 稳定性和版本政策:每个版本的添加和更改列表:版本12.8:版本12.6:版本12.4:版本12.2:版本12.0:版本11.4:版本11.2:版本11.0:版本10.8:版本10.7:版本10.6:版本10.5:版本10.4:
Python线性代数数字图像和小波分析之二
要点
数学方程:数字信号和傅里叶分析,离散时间滤波器,小波分析Python代码实现及应用变换过程: 读取音频和处理音频波,使用Karplus-强算法制作吉他音频离散傅里叶计算功能和绘制图示结果计算波形傅里叶系数正向和反向&…
线性代数笔记10--矩阵的四个基本子空间
0. 引入
矩阵 A m n A_{m \times n} Amn
1. 列空间 C ( A ) C(A) C(A)在 R m R^m Rm中 d i m ( C ( A ) ) p i v o t _ c o l u m n _ c n t r a n k ( A ) r dim(C(A))pivot\_column\_cnt rank(A)r dim(C(A))pivot_column_cntrank(A)r
2. 零空间 N ( A ) N(A) N(A)…
线性代数 --- 特征值与特征向量
特征值与特征向量 已知任意向量x,现有矩阵A对x进行操作后,得到新的向量Ax。这就好比是自变量x与函数f(x)的关系一样,向量x通过类似“函数”的处理得到了一个新的向量Ax。这个新的向量可能和原向量x方向相同,也可能不同(事实上大多…
线性代数笔记11--矩阵空间、秩1矩阵
1. 矩阵空间
所有的 3 3 3 \times 3 33矩阵构成的空间 M M M。
考虑空间 M M M的子空间
上三角矩阵对称矩阵对角矩阵 3 x 3 3x3 3x3矩阵空间的基: [ 1 0 0 0 0 0 0 0 0 ] [ 0 1 0 0 0 0 0 0 0 ] [ 0 0 1 0 0 0 0 0 0 ] [ 0 0 0 1 0 0 0 0 0 ] [ 0 0 0 0 1 0 0 0 0 ] [ 0 0 …
【机器人学导论笔记】四、操作臂逆运动学
4.1 本章任务
本章是将思路逆转过来,已知机械臂的位置和姿态,计算关节角,由此即为逆运动学。
这个任务可以分为两个小问:第一,进行坐标系变换,求出相对于基坐标系{B}的腕部坐标系&…
短视频矩阵系统----矩阵系统源码搭建(技术门槛?)
短视频矩阵是什么意思?短视频矩阵的含义可以理解为全方位的短视频账号,通过不同的账号实现全方位的品牌展示。实际上是指一个短视频账号,通过不同的链接实现品牌展示,在不同的粉丝流量账号中互相转发同一个品牌,在主账…
tiktok矩阵引流系统开发常用源代码!
在数字营销领域,TikTok已成为一个不可忽视的平台,随着其用户基数的不断增长,如何利用TikTok进行有效的引流成为了许多企业和营销人员关注的焦点。
为了实现这一目标,许多开发者开始构建TikTok矩阵引流系统,这些系统通…
DLT算法求解单应性矩阵
DLT算法求解单应性矩阵
原理:
单应性矩阵描述了两个图像之间的投影变换关系,即从一张图到另一张图的变换。
下面是DLT算法的基本原理:
构建投影方程: 对于两个图像中的对应点 ( x , y , 1 ) (x, y, 1) (x,y,1) 和 ( u , v ,…
0102全排列和对换-行列式-线性代数
把n个不同的数排成一列,叫做这n个数的全排列(排列)。 一般情况, 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n是n个数排列的标准次序。 当n个数的任一排列中两个数的先后次序与标准次序不同时,有说有一个逆序。 一个排列中所…
线性代数复习和学习大纲
第一章 向量与复数 1.1 向量的线性运算 1.1.1 向量及其表示 1.1.2 向量的线性运算 1.1.3 向量的共线与共面 1.2 坐标系 1.2.1 仿射坐标系 1.2.2 向量的坐标运算 1.2.3 直角坐标系 1.3 向量的数最积 1.3.1 数量积的定义与性 1.3.2直角坐标系下数量 1.4 向量的向量积 1.4.1 向量积…
0104行列式的性质-行列式-线性代数
记 D ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n ∣ D\begin{vmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\cdots&\cdots&&\cdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\en…
【矩阵】73. 矩阵置零【中等】
矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
解题思路
1、…
Hardness of Scheme-Switching and Comparison in FHE
参考文献:
[AP13] Alperin-Sheriffff, J., Peikert, C.: Practical bootstrapping in quasilinear time. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 1–20. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-…
机器学习中的线性代数
基础知识的的复习:
线性代数——深度学习花书第二章 - 知乎 矩阵分解 特征值分解。 PCA(Principal Component Analysis)分解,作用:降维、压缩。 SVD(Singular Value Decomposition)分解,也叫奇异值分解。 矩阵分解的主要应用是:降维、聚类分析、数据预处理、低维度特征学…
Jacobian matrix雅可比矩阵
参考链接
https://www.youtube.com/watch?vwUF-lyyWpUc&listPLEZWS2fT1672lJI7FT5OXHJU6cTgkSzV2&index6
高数考研 -- 公式总结(更新中)
1. 两个重要极限
(1) lim x → 0 sin x x 1 \lim _{x \rightarrow 0} \frac{\sin x}{x}1 limx→0xsinx1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x ) 1 \lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}1 limf(x)→0f(x)sinf(x)1. (2) lim …
线性代数笔记20--特征值特征向量与旋转矩阵推导
1. 特征向量与特征值
研究对象是一个平面 A A A,向量 X X X通过 A A A变换后仍然平行于 X X X。
这样的向量就叫特征向量。 变换后的向量与原向量的比值就是特征值。 A X / / X A X λ X AX \mathop{//} X\\ AX \lambda X AX//XAXλX
如果矩阵 A A A是奇异矩阵&…
数学与计算机(2)- 线性代数
原文:https://blog.iyatt.com/?p13044
1 矩阵
NumPy 中 array 和 matrix 都可以用于储存矩阵,后者是前者的子类,array 可以表示任意维度,matrix 只能是二维,相当于矩阵专用,在一些矩阵的运算操作上较为直…
《机器学习线性代数基础:Python语言描述》读书笔记----线性方程组的解
有线性方程
化为矩阵乘法的表现形式 Ax[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn][x1x2⋮xn][b1b2⋮bm]bAx \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots &am…
《机器学习线性代数基础:Python语言描述》读书笔记----基底
向量与基底
对于二维向量u[45]u\begin{bmatrix} 4 \\ 5 \end{bmatrix}u[45]来说,一般默认其表示原点到坐标(4,5)的一条有向线段。
这其实基于一个默认的前提:以ex[10]e_x\begin{bmatrix} 1 \\ 0 \end{bmatrix}ex…
线性代数在卷积神经网络(CNN)中的体现
案例:深度学习中的卷积神经网络(CNN) 在图像识别领域,卷积神经网络(Convolutional Neural Networks, CNN)是一个广泛应用深度学习模型,它在人脸识别、物体识别、医学图像分析等方面取得…
2024抖音矩阵云混剪系统源码 短视频矩阵营销系统
2024抖音矩阵云混剪系统源码 短视频矩阵营销系统
矩阵营销系统多平台多账号一站式管理,一键发布作品。智能标题,关键词优化,排名查询,混剪生成原创视频,账号分组,意向客户自动采集,智能回复&am…
MATLAB环境下基于决策树和随机森林的心力衰竭患者生存情况预测
近年来,随着医学数据的不断积累和计算机技术的快速发展,许多机器学习技术已经被用在医学领域,并取得了不错的效果。与传统的基于医学知识经验的心衰预后评估模型相比,机器学习方法可以快速、高效地从繁杂的、海量的心衰病人数据中…
反对称矩阵的特征值及性质
目录写在前面结论反对称矩阵反对称矩阵的特征值是0或纯虚数由性质推导实例推导3x3的反对称矩阵秩为2参考完写在前面
1、文中所有资源、参考已给出来源链接,如有侵权请联系删除 2、码字不易,转载本文请注明出处,本文链接:https://…
高等代数复习:应试经验:求行列式
文章目录 思路总结模板上(下)三角行列式Vandermonde行列式爪型行列式除对角线外各行均相等的行列式三对角行列式 有用的二级结论结论1结论2 个人经验,仅供参考 思路总结
思路1:通过技巧将行列式的形式变好,再归纳地展…
线性代数Python计算:齐二次式二次型矩阵计算
在fxTAxf\boldsymbol{x}^\text{T}\boldsymbol{Ax}fxTAx中,若A(aij)nn\boldsymbol{A}(a_{ij})_{n\times n}A(aij)nn不是对称阵,可以通过构造元素为 aij′aijaji2,1≤i,j≤na_{ij}\frac{a_{ij}a_{ji}}{2},1\leq i,j\leq naij′2aijaji,1≤i,j≤…
线性代数Python计算:无关向量组的正交化
将ℝn^nn的一个无关组α1,α2,⋯,αk\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_kα1,α2,⋯,αk正交化为β1,β2,⋯,βk\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_kβ1,β2,⋯,βk的计算公式为&#x…
线性代数笔记21--对角化、A的幂
1.对角化
对于矩阵 A A A,我们假设有 n n n个向量。 将他们放置在一起组成矩阵 S S S。 A S A [ X 1 X 2 . . . X n ] [ λ 1 X 1 λ 2 X 2 . . . λ n X n ] [ X 1 X 2 . . . X n ] [ λ 1 λ 2 λ 3 ⋱ λ n ] ASA[X_1X_2...X_n][\lambda_1X_1\ \lambda_2X_2...\lambda_n…
线性代数Python计算:矩阵的线性运算
给定正整数mmm和nnn和数域PPP, ∀A(a11a12⋯a1na21a22⋯a2n⋮⋮⋯⋮am1am2⋯amn),B(b11b12⋯b1nb21b22⋯b2n⋮⋮⋯⋮bm1bm2⋯bmn)∈Pmn\forall\boldsymbol{A}\begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ …
线性代数Python计算:矩阵分块
可以通过下标序列来访问numpy的数组a中的片段:a[[i,j]]表示a[i]和a[j],a[:]表示所有元素,a[i:j]表示从a[i]开始直至a[j-1]为止的元素,a[:j]表示从a[0]开始直至a[j-1]为止的元素,a[i:]表示从a[i]开始后的所有元素。 对于…
0105行列式按行(列)展开-行列式-线性代数
在n阶行列式中,把 ( i , j ) 元 a i j (i,j)元a_{ij} (i,j)元aij所在的第 i 行和第 j i行和第j i行和第j列划去后,留下来的 n − 1 n-1 n−1阶行列式叫做 ( i , j ) 元 a i j (i,j)元a_{ij} (i,j)元aij的余子式,记作 M i j M_{ij} Mij&…
线性代数学习笔记(二十四)——向量组的秩(一)
本篇笔记首先回顾了矩阵的秩,然后通过两个例子引入了极大线性无关组的定义,并由极大无关组定义介绍了一些结论,还介绍了相关定理;然后给出了向量组秩的定义,以及一些结论和定理;向量组的秩与矩阵的秩&#…
线性代数学习笔记(十二)——逆矩阵(一)
本篇笔记首先回顾了矩阵的运算,并通过数的除法讨论逆矩阵的引入部分,需要注意:永远不要把矩阵放到分母上!\color{red}{永远不要把矩阵放到分母上!}永远不要把矩阵放到分母上!所以矩阵不存在除法的说法&…
高等代数复习:线性空间
文章目录 线性空间定义和性质线性相关性与秩基与维数矩阵的秩同构坐标子空间解线性方程组 本篇文章适合个人复习翻阅,不建议新手入门使用 线性空间
定义和性质
定义:(线性空间) 设集合 V V V 和数域 K \mathbb{K} K࿰…
工程数学-线性代数-第六版-第一章—行列式学习笔记
目录
一、第一章——行列式 1 二阶与三阶行列式 一、二元线性方程组与二阶行列式 二、三阶行列式 2 全排列和对换 一、排列及其逆序数 二、对换 3 n阶行列式的定义 4 行列式的性质 5 行列式按行(列)展开
二、习题一
三、参考书目 一、第一章——行…
短视频矩阵系统---php7.40版本升级自研
短视频矩阵系统---php7.40版本升级自研
1.部署及搭建
相对于其他系统,该系统得开发及部署难度主要在各平台官方应用权限的申请上,据小编了解,目前抖音短视频平台部分权限内侧名额已满,巧妇难为无米之炊,在做相关程序…
计算两帧雷达数据之间的变换矩阵
文章目录 package.xmlCMakeLists.txtpoint_cloud_registration.cc运行结果 package.xml
<?xml version"1.0"?>
<package format"2"><name>point_cloud_registration</name><version>0.0.0</version><descriptio…
线性代数笔记8--AX=b:可解性、解的结构
1. 求解Axb A X b AXb AXb有解,则 b b b在 A A A的列向量之中。
举例 A X b [ 1 2 2 2 2 4 6 8 3 6 8 10 ] [ x 1 x 2 x 3 x 4 ] [ b 1 b 2 b 3 ] AXb\\ \begin{bmatrix} 1 & 2 & 2 & 2\\ 2 & 4 & 6 & 8\\ 3 & 6 & 8 & 10…
0103n阶行列式-行列式-线性代数
文章目录 一 n阶行列式二 三阶行列式三 特殊行列式结语 一 n阶行列式 ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a n 1 a n 2 ⋯ a n n ∣ \begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\cdots&\cdots…
1572.矩阵对角线元素的和
刷算法题:
第一遍:1.看5分钟,没思路看题解
2.通过题解改进自己的解法,并且要写每行的注释以及自己的思路。
3.思考自己做到了题解的哪一步,下次怎么才能做对(总结方法)
4.整理到自己的自媒体平台。
5.再刷重复的类…
线性代数笔记18--行列式公式、代数余子式
1. 行列式公式推导
二阶行列式推导 [ a b c d ] [ a 0 c d ] [ 0 b c d ] [ a 0 0 d ] [ a 0 c 0 ] [ 0 b c 0 ] [ 0 b 0 d ] [ a 0 0 d ] − [ b 0 0 c ] a d − b c \begin{align} \begin{bmatrix} a & b \\ c & d \end{bmatrix}& \begin{bmatrix} a &…
使用cuBLAS做行优先矩阵的矩阵乘
TL;DR
总结:如果你的A、B矩阵都是以行优先的方式去存的,最终想得到行优先的结果矩阵C,那么请放心使用cuBLAS(虽然它要求我们以列优先格式存储),但要注意参数的填写!!!。…
0201线性方程组和矩阵-矩阵及其运算-线性代数
文章目录 一、线性方程组二、矩阵的定义结语 一、线性方程组
设有 n 个未知数 m n个未知数m n个未知数m个方程的线性方程组 { a 11 x 1 a 12 x 2 ⋯ a 1 n x n b 1 , a 21 x 1 a 22 x 2 ⋯ a 2 n x n b 2 , ⋯ a m 1 x 1 a m 2 x 2 ⋯ a m n x n b m , \begin{ca…
子矩阵(蓝桥杯,acwing,单调队列)
题目描述:
给定一个 nm(n 行 m 列)的矩阵。
设一个矩阵的价值为其所有数中的最大值和最小值的乘积。
求给定矩阵的所有大小为 ab (a 行 b 列)的子矩阵的价值的和。
答案可能很大,你只需要输出答案对 99…
LDL^H分解求逆矩阵与MATLAB仿真(Right-Looking)
通过分解将对称正定厄米特矩阵分解成下三角矩阵L和对角矩阵D来求其逆矩阵 目录
前言 一、LDL^H基本算法
二、LDL^H Right-Looking算法
三、D矩阵求逆
四、L矩阵求逆
五、A矩阵求逆
六、计算量分析
七、MATLAB仿真
八、参考资料
总结 前言 在线性代数中,LDL…
【代码随想录 | 数组 05】螺旋矩阵 ||
文章目录 5.螺旋矩阵25.1题目5.2思路 5.螺旋矩阵2
5.1题目
59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。 示例一:
输入:n 3
输出ÿ…
【算法】【数组与矩阵模块】不包含本位置的累乘数组值(含不用除法的方法)
目录前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本思考感悟写在最后前言
当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介绍 …
基于矩阵求导的线性回归
矩阵求导 考虑矩阵乘法 A⋅BCA \cdot B C A⋅BC 考虑Loss函数 L∑im∑jn(Cij−p)2L \sum^m_{i}\sum^n_{j}{(C_{ij} - p)^2} Li∑mj∑n(Cij−p)2 考虑C的每一项导数 ▽Cij∂L∂Cij\triangledown C_{ij} \frac{\partial L}{\partial C_{ij}} ▽Cij∂Cij∂L 考虑…
信号与系统之《一文看懂傅里叶变换》
“傅里叶变换是一种非常有用的数学工具,它可以将一个复杂的信号分解成许多简单的频率成分。傅里叶变换在信号处理、图像处理、音乐、视频和通信等许多领域都有广泛的应用。相信大部分同学在毕业之后的一段时间之内都还没有理解到傅里叶变换的精髓,今天我…
李雅普诺夫方程以及MATLAB函数求解
一、李雅普诺夫方程
1. 离散时间系统lyapunov方程:
(1)开环系统:x(k1)Ax(k)Bu(k)
ATPA - P -Q
(2)闭环系统:x(k1)Ax(k)Bu(k)
(A-BK)TP(A-BK) - P -Q
2. 连续时间系统lyapunov方程&#…
【泛函分析】存在有可列个间断点的单调函数
下面列举一个定义在 [0,1][0,1][0,1] 上的单调递增函数 fff, 它在 [0,1][0,1][0,1] 上具有可列个不连续点.
定义 f(x)1f(x)1f(x)1, ∀x∈[0,12]\forall x\in [0, \frac{1}{2}]∀x∈[0,21] 定义 f(x)2f(x)2f(x)2, ∀x∈(12,23]\forall x\in (\frac{1}{2}, \frac{2}{3}]∀x∈(…
NumPy之矩阵、向量、线性代数等的操作
NumPy之矩阵、向量、线性代数 NumPy矩阵和向量矩阵向量创建向量创建矩阵访问元素转置矩阵矩阵加减乘除矩阵向量乘法矩阵求逆矩阵的迹向量点积向量范数 NumPy线性代数计算矩阵乘积计算矩阵的逆解线性方程组 NumPy矩阵和向量
矩阵 在NumPy中,矩阵可以看作是一个二维数…
MATLAB开发中的常见问题和解决方法:如何解决常见的性能和bug问题
章节一:引言
在MATLAB开发中,经常会遇到一些常见的性能和bug问题。这些问题可能导致程序运行缓慢、结果不准确或者甚至崩溃。本文将介绍一些常见问题,并提供解决方法和案例,帮助开发者更好地应对这些挑战。
章节二:性…
【学习笔记】[PA 2022] Drzewa rozpinające
单纯只是为了记录一下这个 trick \text{trick} trick。而且涉及到一点分块矩阵的思想,感觉还挺有意思的。
矩阵行列式引理:设 A A A为可逆矩阵, u , v u,v u,v为列向量,则有: det ( A u v T ) det ( A ) ( 1 v T A…
CUDA编程模型系列六(利用shared memory和统一内存优化矩阵乘)
CUDA编程模型系列六(利用shared memory和统一内存优化矩阵乘) 本系列教程将介绍具体的CUDA编程代码的细节 CUDA编程模型系列六(利用shared memory和统一内存优化矩阵乘) #include <stdio.h>
#include <math.h>// a[][] * b[][] c[][]
//
// …
强化学习之Makov决策
离散时间Makov决策过程
离散时间的Markov决策过程模型可以在离散时间的智能体/环境接口的基础上进一步引入具有Markov性的概率模型得到。
奖励,汇报和价值函数
对于回合制任务,驾驶某一回合在第t步达到终止状态,则从步骤t(t<T)以后的回报ÿ…
SMiC矩阵将于3月6日正式上线,开启数字化经济新纪元
在数字化浪潮的推动下,全球瞩目的SMiC矩阵将于2024年3月6日正式上线。这一里程碑式的事件标志着数字化经济迈入了一个全新的时代,为思洣客、合作伙伴和整个经济生态带来了前所未有的机遇和挑战。
SMiC矩阵作为引领数字化经济的新力量,始终致…
MATLAB----矩阵的索引
文章目录1. 获取矩阵中单个元素2. 获取矩阵中多个元素3. 使用冒号运算符获取元素1. 获取矩阵中单个元素
m [ 1 2 3; 4 5 6; 7 8 9 ]
m(1) % 索引从1开始
m(8) % 列方向索引,第八个,6m(2,3) % 获取第二行第三列的元素
% 第一个参数为行,第二…
两个复高斯分布的乘积(高维)
假设p(x)∝CN(μ1,Σ1)CN(μ2,Σ2)p(\boldsymbol x) \propto \mathcal{CN}(\boldsymbol \mu_1, \boldsymbol \Sigma_1)\mathcal{CN}(\boldsymbol \mu_2, \boldsymbol \Sigma_2)p(x)∝CN(μ1,Σ1)CN(μ2,Σ2),有 p(x)∝exp{−(x−μ1)HΣ1−1(x−μ1)−(x−…
《机器学习线性代数基础:Python语言描述》读书笔记----相似矩阵与相似变换
坐标取决于基底
结合前面知识,可知,坐标的表示使是基于 基底的。
书中给出一个例子:对于一个物体,它是客观存在的(类比:某个指定向量在空间中的绝对位置)。但是,如果换一个角度 看…
ICP變種Point-To-Plane算法推導
ICP變種Point-To-Plane算法推導前言損失函數R,t參數化最小二乘問題求解Moore–Penrose偽逆SVD矩陣分解前言
接續ICP(Iterative Closest Point)算法推導,本篇介紹ICP的變種Point-To-Plane損失函數及其求解方法。
本文同樣整理自深藍學院三維…
短视频seo矩阵+抖音小程序源码开发解决方案(一)
该解决方案主要针对产品用户交易决策周期长/非标定制等情况的企业,如:房产、汽车、金融、咨询服务,广告设计、网络科技公司,TOB类销售行业等。
基于不同的经营场景,解决方案全面更新,新增账号管理…
C++学习日记#6——牛顿插值公式
Lagrange插值多项式,公式结构紧凑,理论分析方便,但插值节点增减时全部插值及函数均要随之变换,实际计算不方便。借此引入牛顿插值公式。
均差表计算公式: 均差表
xif(xi)一阶均差二阶均差...n阶均差x0f(x0)...x1f(x1…
线性代数Python计算:矩阵的转置、方阵的行列式和方阵的逆
1.矩阵的转置
numpy用来表示矩阵的2维数组的array对象的T属性,返回矩阵的转置。 例1 设A(201132)\boldsymbol{A}\begin{pmatrix}2&0&1\\1&3&2\end{pmatrix}A(210312),B(17−1423201)\boldsymbol{B}\begin{pmatrix}1&7&-1…
线性代数学习笔记(二十九)——方程组解的结构(一)
停更2年多了,做事得有始有终,继续更新。。。
本篇笔记回顾了线性方程组解的三种情况,并讨论了齐次线性方程组解的结构,并介绍了齐次线性方程组解的相关性质。其中重点讨论了基础解系定义,以及基础解系的求法和解题步骤…
线代 | 【提神醒脑】自用笔记串联二 —— 向量组 · 线性方程组 · 特征值与特征向量
本文总结参考于 kira 2023 线代提神醒脑技巧班。 笔记均为自用整理。加油!ヾ(◍∇◍)ノ゙ 四、向量组 4.1、向量组的线性相关性 ----------------------------------------------------------------------------------------------------------…
28线性空间02—— 坐标变换
💖💖感谢各位观看这篇文章,💖💖点赞💖💖、收藏💖💖、你的支持是我前进的动力!💖💖 💖💖感谢你的阅读💖,专栏文章💖持续更新!💖关注不迷路!!💖 矩阵线性代数笔记整理汇总,超全面 文章目录 坐标变换参考线性空间01——线性空间、线性相关、…
斐波那契数列的矩阵乘法方法
1、求斐波那契数列矩阵乘法的方法
1.1 斐波那契数列的线性求解(O(n)O(n)O(n))的方法
//斐波那契数列:1 1 2 3 5 8 ...
int fibonacci(int n) {if (n < 1) return 0;if (n 1 || n 2) return 1;int a 1, b 1, c 0;for (int i 3; i &…
MATLAB-三维插值运算
MATLAB中是支持三维及三维以上的高维插值的。三维插值的基本原理与一维插值和二维插值是一样的,但三维插值是对三维函数进行的插值。在MATLAB中,使用interp3函数实现插值,其调用格式如下。vi interp3(x,y,z,v,xi,yi,zi) %返回值 vi是三维插值…
几何学小课堂:非欧几何(广义相对论采用黎曼几何作为数学工具)【学数学关键是要学会在什么情况下,知道使用什么工具。】
文章目录 引言I 非欧几何1.1 黎曼几何1.2 共形几何1.3 罗氏几何II 黎曼几何的应用2.1 广义相对论2.2 超弦III 理解不同的几何体系的共存3.1 更扎实的欧氏几何3.2 殊途同归引言
公理有错会得到两种情况: 如果某一条自己设定的新公理和现有的公理相矛盾,那么相应的知识体系就建…
40行MATLAB代码实现卡尔曼滤波-简单易懂
1 前言最近学习了卡尔曼滤波,体会到了数据融合下进行最优估计的思想。如果你也是小白,可以通过这个例子自己动手感受数据融合。学习资料参考B站大神DR_CAN博士,连接:【卡尔曼滤波器】直观理解与二维实例2 案例基于上述视频中Excel…
线性代数的本质(六)——线性空间
文章目录 线性空间线性空间子空间坐标与同构线性变换与矩阵基变换与坐标变换 线性空间
线性空间 Grant: 普适的代价是抽象。 仔细分析就会发现,关于向量空间的一切概念及有关定理都不依赖于向量的具体表现形式(有序数组),也不依赖于向量加法、数乘的具体…
线段树维护矩阵:0920T4
正解为文艺平衡树维护矩阵,但我打不动,所以打了部分分
首先可以写成dp形式
然后又可以写成矩阵形式
然后矩阵显然支持结合律
所以可以拿线段树维护
#include<bits/stdc.h>
using namespace std;
#define int long long
inline int read(){int…
【论文写作】符号:矩阵、向量的乘法、内积、点积等
【论文写作】符号:矩阵、向量乘法、内积、点积等 文章目录 【论文写作】符号:矩阵、向量乘法、内积、点积等1. 矩阵乘法1.1 矩阵乘积1.2 矩阵哈德玛乘积1.3 矩阵克罗内克积 2. 向量乘法2.1 向量点积、内积2.2 向量Hadamard积2.3 向量外积2.4 向量叉积 1.…
2024通信保研-电磁场电磁波复习
标量场的梯度的旋度恒等于0,旋度的散度等于0。 旋度: rot F ( e x ∂ ∂ x e y ∂ ∂ y e z ∂ ∂ z ) ( e x F x e y F y e z F z ) e x ( ∂ F z ∂ y − ∂ F y ∂ z ) e y ( ∂ F x ∂ z − ∂ F z ∂ x ) e x ( ∂ F y ∂ x − ∂ F x …
【Python · PyTorch】线性代数 微积分
本文采用Python及PyTorch版本如下: Python:3.9.0 PyTorch:2.0.1cpu
本文为博主自用知识点提纲,无过于具体介绍,详细内容请参考其他文章。 线性代数 & 微积分 1. 线性代数1.1 基础1.1.1 标量1.1.2 向量长度&…
求矩阵高次幂的两种“另类”方法
文章目录 【方法一】运用哈密顿凯莱定理相关例题 【方法二】运用特征方程二阶矩阵求解通法三阶矩阵求解通法相关例题 市面上许多资料给出的计算矩阵高次幂的方法,无外乎有这几种:
分块矩阵求解高次幂;先求低次方幂,然后通过找规律…
线性代数笔记26--正定矩阵、最小值
1. 正定矩阵
判断正定矩阵
对于二阶的来说 A [ a b c d ] A \begin{bmatrix} a & b \\ c & d \end{bmatrix} A[acbd]
判定条件 λ 1 > 0 , λ 2 > 0 \lambda_1 \gt 0,\lambda_2 \gt 0 λ1>0,λ2>0 a > 0 , a c − b 2 > 0 a \gt0,ac-b^2…
python-np.linalg-线性代数
文章目录 一、线性代数计算的函数1. 矩阵和向量的乘法:np.dot()2. 矩阵的逆:np.linalg.inv(A)3. 矩阵的转置:np.transpose(A)4. 矩阵的行列式:np.linalg.det(A)5. 矩阵的特征值和特征向量:np.linalg.eig()6. 解线性方程…
线性代数(二)| 行列式性质 求值 特殊行列式 加边法 归纳法等多种方法
文章目录 1. 性质1.1 重要性质梳理1.1.1 转置和初等变换1.1.2加法行列式可拆分1.1.3 乘积行列式可拆分 1.2 行列式性质的应用1.2.1 简化运算1.2.2 将行列式转换为(二)中的特殊行列式 2 特殊行列式2.1 上三角或下三角行列式2.2 三叉行列式2.3 行列式行和&…
线性代数本质系列(二)矩阵乘法与复合线性变换,行列式,三维空间线性变换
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第二篇
向量究竟是什么? 向量的线性组合,基与线性相关 矩阵与线性相关 矩阵乘法与复合线性变换 三维空间中的线性变换 行列式 逆矩阵,列空间,秩与零空间 克…
0204克拉默法则-矩阵及其运算-线性代数
含有n个未知数 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn的n个线性方程的方程组 { a 11 x 1 a 12 x 2 ⋯ a 1 n x n b 1 , a 21 x 1 a 22 x 2 ⋯ a 2 n x n b 2 , ⋯ ⋯ , a n 1 x 1 a n 2 x 2 ⋯ a n n x n b n , \begin{cases} a_{11}x_1a_{1…
面试算法-154-搜索二维矩阵 II
题目
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。 每列的元素从上到下升序排列。
示例 1:
输入:matrix [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,…
短视频抖音账号矩阵系统源码开发者自研(二)
一、短视频账号矩阵系统源码开发储存集群化开发运转更快
短视频账号矩阵系统源码开发采用储存集群化开发,可以显著提高系统的运转速度和效率。通过优化储存结构和算法,系统能够更快地处理短视频账号数据,确保用户能够流畅地浏览和观看短视频…
[Eigen中文文档] 预处理器指令
文档总目录 本文目录 具有重大影响的宏C 标准特性断言对齐、矢量化和性能调整插件Eigen 开发人员的宏 英文原文(Preprocessor directives)
你可以通过定义预处理器宏来控制Eigen的某些方面。这些宏应该在包含任何Eigen头文件之前定义。通常最好在项目选项中设置它们。
本页面…
最小二乘法拟合平面原理MATLABC++实现
文章目录最小二乘法拟合平面原理MATLAB&C实现最小二乘法拟合平面原理MATLAB实现c实现最小二乘法拟合平面原理MATLAB&C实现
最小二乘法拟合平面原理 最小二乘法是我们平时用的比较的多一种拟合算法,尤其是在直线拟合,平面拟合中,大量…
【计算方法与科学建模】矩阵特征值与特征向量的计算(五):乘幂法的加速(带有原点移位的乘幂法)
文章目录 一、Jacobi 旋转法二、Jacobi 过关法三、Householder 方法四、乘幂法四、乘幂法的加速 矩阵的特征值(eigenvalue)和特征向量(eigenvector)在很多应用中都具有重要的数学和物理意义。 本文将详细介绍乘幂法的基本原理和步…
编程零基础算法 | 四、循环和选择结构——1572. 矩阵对角线元素的和
一、题目链接
1572. 矩阵对角线元素的和
二、题目简介
给你两个整数,n 和 start 。 数组 nums 定义为:nums[i] start 2*i(下标从 0 开始)且 n nums.length 。 请返回 nums 中所有元素按位异或(XOR)后…
【线性代数】通过矩阵乘法得到的线性方程组和原来的线性方程组同解吗?
一、通过矩阵乘法得到的线性方程组和原来的线性方程组同解吗?
如果你进行的矩阵乘法涉及一个线性方程组 Ax b,并且你乘以一个可逆矩阵 M,且产生新的方程组 M(Ax) Mb,那么这两个系统是等价的;它们具有相同的解集。这…
【矩阵快速幂】封装类及测试用例及样例
作者推荐
视频算法专题
通俗的说,就是矩阵的乘方。
封装类
核心代码
class CMat
{
public:// 矩阵乘法static vector<vector<long long>> multiply(const vector<vector<long long>>& a, const vector<vector<long long>…
c JPEG 1D DCT 优化二(AAN)
这两个图可能就是AAN 的数学模型 优化DCT就是用代码实现矩阵9,10
9和10已经把64个系数缩小到一半32个了。光从这两图可看出,优化后乘法少了64-32436个,加法少了64-32-824。估计优化时间可少百分之40左右。o[0]的4个cos系数都是1,可省4个乘法…
解线性方程组的各种情况
解线性方程组的各种情况讨论。本文主要介绍解线性方程组的各种情况以及解的情况。已知线性方程组的形式如下 AxbAxbAxb
其中AAA是一个mnm\times nmn矩阵。根据AAA的性质, 解的情况有好几种。根据n,mn,mn,m之间的大小, 我们可以把AAA矩阵分为三种情况 mn…
数学分析第六课(域以及域的性质)
In this lecture, we shall introduce an important concept which is called field.
Definition: A field is a set FFF with two operations, called addtion and multiplication, which satisfy the following so-called field axionms. Axioms for addition ∀x,y(x,y∈F)…
cplex求解线性规划(python)
前言
Cplex是IBM公司的一款商业求解器,其求解性能十分强大,在整数规划领域有突出表现。Cplex支持多种语言调用,包括C,java,python等,之前写过C安装以及调用Cplex的教程,本文将简单介绍Cplex在p…
基于Cplex的分支定价
前言
分支定界(branch and bound)和分支定价(branch and price)仅一字之差,这两者之间也有着紧密联系,简单来说分支定价分支定界列生成。个人觉得在运筹学领域,分支定价算法也算是比较高级的算…
一个概率论例题引发的思考
浙江大学版《概率论与梳理统计》一书中的,第13章第1节例2如下:
这个解释和模型比较简单易懂。接下来,第2节的例2是一个关于此模型的题目: 在我自己的理解中,此题的解法跟上一个题目一样,第二级传输后&…
【算法题】螺旋矩阵II (求解n阶Z形矩阵)
一、问题的提出
n阶Z形矩阵的特点是按照之(Z)字形的方式排列元素。n阶Z形矩阵是指矩阵的大小为nn,其中n为正整数。
题目描述
一个 n 行 n 列的螺旋(Z形)矩阵如图1所示,观察并找出填数规律。 图1 7行7列和8行8列的螺旋(Z形)矩阵
现在给出矩阵大小 n&…
机器学习线性代数基础
本文是斯坦福大学CS 229机器学习课程的基础材料,原始文件下载 原文作者:Zico Kolter,修改:Chuong Do, Tengyu Ma 翻译:黄海广 备注:请关注github的更新,线性代数和概率论已经更新完毕…
伴随矩阵的特征值跟原矩阵特征值居然有关系!!!附证明
文章目录 论点:A与其伴随矩阵的特征值相乘等于|A|证明证明证明中涉及的相关定理:1.逆矩阵与伴随矩阵的关系2.A可逆时,A的逆矩阵的特征值是原矩阵特征值的倒数 论点:A与其伴随矩阵的特征值相乘等于|A| 证明
证明 证明中涉及的相关…
矩阵乘法(C++ mpi 并行实现)
矩阵乘法有2种思路,我最先想到的是第一种思路,但是时间、空间复杂度都比较高。后面参考了一些资料,实现了第二种思路。
一、思路1:按行、列分块
矩阵乘法有一个很好的性质,就是结果矩阵的每个元素是不互相依赖的&…
leetcode59. 螺旋矩阵 II(java)
螺旋矩阵 题目描述缩进法 上期经典 题目描述 难度 - 中等 原题链接 - 螺旋矩阵 示例1: 输入:n 3 输出:[[1,2,3],[8,9,4],[7,6,5]] 示例 2: 输入:n 1 输出:[[1]] 提示: 1 < n < 20 缩进法…
LA@齐次线性方程组解的结构
文章目录 齐次线性方程组解的结构🎈解的性质齐次线性方程组的解的线性组合还是方程组的解基础解系通解 定理:齐次线性方程组基础解系存在定理齐次线性方程组的基础解系包含的向量个数(秩)👺应用和示例推论1推论2推论3:转置矩阵对的乘积秩的性质非自由未知…
LA@二次型分类@正定二次型@主子式
文章目录 abstract引言正定二次型小结可逆线性变换不改变二次型的正定性二次型是正定的充要条件推论:正定矩阵和特征值正定二次型(正定矩阵)性质 负定二次型负定二次型判定条件 k阶顺序主子式赫尔维茨定理:主子式判定二次型正定性和负定性 二次型分类小结有定二次型不定二次型 …
【图形学】投影和消隐简介
投影
正交投影
对于物体上任意一点的三维坐标P(x,y,z),投影后的三维坐标为 P ′ ( x ′ , y ′ , z ′ ) P^\prime(x^\prime,y^\prime,z^\prime) P′(x′,y′,z′),那么正交投影的方程为 { x ′ x y ′ y z ′ 0 \begin{cases} x^\primex\\y^\primey\\z^\prime0 \end{case…
householder进行矩阵QR分解
文章目录 1. Householder 进行QR分解 1. Householder 进行QR分解 A Q R (1) AQR\tag1 AQR(1) A [ 1 2 0 1 1 0 3 1 1 0 3 2 1 2 0 2 ] (2) A\begin{bmatrix}1&2&0&1\\\\1&0&3&1\\\\1&0&3&2\\\\1&2&0&2\end{bmatrix}\tag2 A…
【线性代数与矩阵论】坐标变换与相似矩阵
坐标变换与相似矩阵
2023年11月4日 #algebra 文章目录 坐标变换与相似矩阵1. 基变换与坐标变换2. 相似变换下链 1. 基变换与坐标变换
坐标变换与基变换都要通过过渡矩阵 A A A 来实现。设有一向量 f ⃗ \vec f f , x x x 是在基 α \alpha α 下该向量的坐标…
雅可比矩阵(Jacobian Matrix)
假设给定一个从n维欧式空间到m维欧式空间的变换: 雅可比矩阵就是将一阶偏导数排列成一个m行、n列形式的矩阵,记作: 举一个例子: 雅可比矩阵等于:
分块矩阵知识点整理:
1.分块方法:横竖线不能拐弯,思想为将矩阵分块看作向量计算
2.标准型 不一定是方的 特殊性:经过分块后会出现单位矩阵和0矩阵
3.分块矩阵的运算: 1.加减乘的运算与向量运算相同
4.分块矩阵求转置: 1.将子块看作普通元素求转置 2…
LA@线性代数学习总结@主要对象和问题@思想方法
文章目录 线性代数研究对象主要问题联系核心概念核心定理 核心操作和运算基础高级小结 性质和推导方法问题转换为线性方程组求解问题验证和推导性质定理 线性代数研究对象
线性代数的研究对象主要是行列式和矩阵(向量)矩阵这种对象可以做的操作和运算很多,特别是方阵,它们的计…
【ICCV2023】MMVP:基于运动矩阵的视频预测
目录
导读
本文方法
步骤1:空间特征提取
步骤2:运动矩阵的构造和预测
步骤3:未来帧的合成和解码
实验
实验结果
消融实验
结论 论文链接:https://openaccess.thecvf.com/content/ICCV2023/html/Zhong_MMVP_Motion-Matrix…
Jacobi迭代与SOR迭代求解希尔伯特矩阵
给出线性方程组 Hn*x b,其中系数矩阵Hn为希尔伯特矩阵: 假设 x ∗ (1, 1, . . . , 1)T,b Hnx ∗。若取 n 6,8, 10,分别用 Jacobi 迭代法及 SOR迭代(ω 1, 1:25,1:5)求解,比较计算结果。…
单细胞seurat入门—— 从原始数据到表达矩阵
根据所使用的建库方法,单细胞的RNA序列(也称为读取(reads)或标签(tags))将从转录本的3端(或5端)(10X Genomics,CEL-seq2,Drop-seq&…
MIT线性代数笔记-第31讲-线性变换及对应矩阵
目录 31.线性变换及对应矩阵打赏 31.线性变换及对应矩阵
线性变换相当于是矩阵的抽象表示,每个线性变换都对应着一个矩阵
例: 考虑一个变换 T T T,使得平面上的一个向量投影为平面上的另一个向量,即 T : R 2 → R 2 T:R^2 \to R…
短视频矩阵系统源码是如何运作的?
在当今数字化时代,短视频已经成为人们日常生活中的重要娱乐方式。而为了更好地满足用户需求以及提升使用体验,短视频平台需要依靠一个强大而高效的短视频矩阵系统。那么,这个系统又是如何运作的呢?
首先,短视频矩阵系…
【学习笔记】插值之拉格朗日插值(Lagrange)
0 插值介绍
插值法是广泛应用于理论研究和工程实际的重要数值方法。用提供的部分离散的函数值来进行理论分析和设计都是极不方便的,因此希望能够用一个既能反映原函数特征,有便于计算的简单函数去近似原函数。
1 低次拉格朗日插值
定理:设…
线性代数笔记1 12.30
学习视频: 1.4 行列式的计算(一)_哔哩哔哩_bilibili 以下内容,包含:
二阶三阶行列式
n阶行列式
行列式的性质
行列式按行展开
【视觉SLAM十四讲学习笔记】第三讲——旋转向量和欧拉角
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵 【视觉SLAM十四讲学习笔记】第三讲——Eigen库 本章将介绍视觉SLAM的基本问题之一:如何…
抖去推--短视频账号矩阵系统saas工具源码技术开发
一、短视频矩阵系统搭建常见问题? 1、抖去推的短视频AI矩阵营销软件需要一定的技术水平吗?
答:不需要。产品简单易用,不需要具备专业的技术水平,即使是初学者,也能够轻松上手操作。
3、抖去推的短视频AI矩…
Hermite矩阵的特征值估计——courant-fischer定理
Hermite矩阵的特征值估计——courant-fischer定理
一、courant-fischer定理(min-max定理)
将hermite矩阵的特征值表示为一系列最优化问题的解。
一个函数 R ( x ) x H A x x H x R(x)\frac{x^HAx}{x^Hx} R(x)xHxxHAx,称为Rayleigh商&am…
已知线段和线外一点p,求点p1,使得p,p1线段和原有线段平行
已知线段和线外一点p,求点p1,使得p,p1线段和原有线段平行
这里不做详细公式推导,主要是我也忘了
只列出代码,方便以后使用
该函数依赖于已知一个点和一个线段,求点到线段的垂足
QPointF CMeasureAlgori…
【PID学习笔记 4 】控制系统基础之三
写在前面
上一篇以一个经典的水温调节系统为案例,学习怎样对一个实际的应用进行数学建模。本文重点介绍负反馈原理的概念、控制系统的组成与分类、控制系统的基本要求。
一、负反馈原理
将系统的输出信号引回输入端,与输入信号相比较,利用…
线性代数——行列式按行(列)展开
目录
一、余子式:将行列式某元素所在行和列的元素全去掉 剩余部分所构成的行列式,称为该元素的余子式
二、代数余子式
三、行列式等于它的任一行(列)的各元素与对应代数余子式乘积之和
四、行列式某行元素(列&…
求斐波那契数列矩阵乘法的方法
斐波那契数列
先来简单介绍一下斐波那契数列: 斐波那契数列是指这样一个数列:1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始 &…
MIT线性代数笔记-第28讲-正定矩阵,最小值
目录 28.正定矩阵,最小值打赏 28.正定矩阵,最小值
由第 26 26 26讲的末尾可知在矩阵为实对称矩阵时,正定矩阵有以下四种判定方法(都是充要条件):
所有特征值都为正左上角所有 k k k阶子矩阵行列式都为正&…
【原创】【一类问题的通法】【真题+李6卷6+李4卷4(+李6卷5)分析】合同矩阵A B有PTAP=B,求可逆阵P的策略
【铺垫】二次型做的变换与相应二次型矩阵的对应:二次型f(x1,x2,x3)xTAx,g(y1,y2,y3)yTBy ①若f在可逆变换xPy下化为g,即P为可逆阵,有P…
数组|73. 矩阵置零 48. 旋转图像
73. 矩阵置零
**题目:**给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 题目链接:矩阵置零
class Solution {public void setZeroes(int[][] matrix) {Stack<int[]> mapofzerone…
【矩阵】73. 矩阵置零
题目
法1:自己想的笨蛋方法
class Solution {public void setZeroes(int[][] matrix) {Set<Integer> rowSet new HashSet<>();Set<Integer> columnSet new HashSet<>();for (int i 0; i < matrix.length; i) {for (int j 0; j <…
代码随想录算法训练营第二天(C) | 977.有序数组的平方 209.长度最小的子数组 59.螺旋矩阵
文章目录 前言一、977.有序数组的平方二、209.长度最小的子数组三、59.螺旋矩阵总结 前言
java版:
代码随想录算法训练营第二天 | 977.有序数组的平方 ,209.长度最小的子数组 ,59.螺旋矩阵_愚者__的博客-CSDN博客 一、977.有序数组的平方
…
Rust 开源线性代数库 nalgebra_linsys
nalgebra_linsys 是 Rust 中 nalgebra 生态系统的一部分,它专注于线性系统的求解。这个库提供了用于解决线性方程组、最小二乘问题以及进行线性代数系统分析的工具。
nalgebra_linsys 库建立在 nalgebra 库的基础上,nalgebra 本身是一个强大的线性代数库…
线性代数笔记15--投影矩阵和最小二乘法
1. 投影矩阵
投影矩阵 P A ( A ⊤ A ) − 1 A ⊤ PA(A^{\top}A)^{-1}A^{\top} PA(A⊤A)−1A⊤ p P b pPb pPb
当 b ⊥ C ( A ) b\perp C(A) b⊥C(A), p A ( A ⊤ A ) − 1 A ⊤ b 0 ; p 0 pA(A^{\top}A)^{-1}A^{\top}b0;p0 pA(A⊤A)−1A⊤b0;p0当 b ∈ C ( A ) , A X …
线性代数(一)——向量基础
向量基础 1、向量和线性组合2、向量的模和点乘3、矩阵4、参考 线性代数的核心是向量的加和乘两种运算的组合,本篇博客为线性代数的一个引子,主要从向量、线性组合和矩阵逐步引出线性代数的相关知识。 1、向量和线性组合
首先介绍的是向量相关࿰…
SfM——八点法计算F矩阵(基础矩阵)与三角测量
1 八点法计算F矩阵(基础矩阵)
基础矩阵用于描述两个视图之间的几何关系 基础矩阵:基础矩阵 F F F 是描述两个视图之间相机投影关系的矩阵。对于两个对应的图像坐标点 ( x , y , 1 ) (x, y, 1) (x,y,1) 和 ( u , v , 1 ) (u, v, 1) (u,v,1…
MIT线性代数-方程组的几何解释
文章目录 1. 二维空间1.1 行方向1.2 列方向 2. 三维空间2.1 行方向2.2 列方向 假设有一个方程组 A X B AXB AXB表示如下 2 x − y 0 (1) 2x-y0\tag{1} 2x−y0(1) − x 2 y 3 (2) -x2y3\tag{2} −x2y3(2) 矩阵表示如下: [ 2 − 1 − 1 2 ] [ x y ] [ 0 3 ] (3)…
MATLAB模拟矩阵法绘制多层薄膜反射率与波长关系曲线
1.程序流程
1.输入参数
中心波长λ0入射介质折射率n0基片折射率ng膜层数量x依次输入n1、n2、n3…并且每输入一次n,选择一次该膜层对应的光学厚度入射角theta,并转化为弧度制
2.计算各层参数
由折射定律计算每一层的折射角计算每一层的ηp和ηs计算基…
ORB-SLAM之SVD奇异值分解——理论 (一)
在学习《视觉SLAM十四讲》过程中常遇到SVD奇异值分解,经过一段时间的学习,在此进行记录整理, 本篇主要整理SVD的数学理论基础, 下一篇 进行整理 SVD 实际应用 。
一、线性代数的方阵分解
给定一大小为 m m m\times m mm 的矩阵 A A A(方阵…
矩阵理论的概念间的组合关系的公式
矩阵理论的概念间的组合关系的公式
现在很火执的人工智能技术,要求很高的数学基础知识。 除了微积分就是线性代数的内容了。自动微分框架是人工 智能技术的底层框架。其实就是实现了微积分的各种函数 的微积分运算而矣。线性代数的内容应用于计算机 的软件中的各个…
蓝桥备赛——矩阵读入
题目描述 如上图所示,是一道有关二维前缀和的问题,因为涉及到二维,肯定就是以矩阵的形式进行读入的。
为此,针对矩阵的读入形式进行总结,可以大致总结出两种类型如下:
二维列表推导式
n, m, k map(int…
【cuda】三、矩阵相乘与coalescing writes(合并写操作)
Matrix Multiplication and Optimization
线程块
功能
并行执行:线程块是一组同时执行的线程。它们共同执行分配给它们的任务资源共享:线程块内的线程可以共享数据和同步执行。通过共享内存(Shared Memory)和同步原语ÿ…
矩阵行列式的四大应用
目录
一. 介绍
二. 行列式的基本性质
2.1 单位阵的行列式
2.2 交换行位置的行列式
三. 矩阵求逆与行列式
四. 体积与行列式
五. 矩阵主元与行列式
六. 解方程与矩阵行列式
七. 小结 一. 介绍
行列式可以反应矩阵的很多性质,比如可以求矩阵的逆,…
线性代数——(期末突击)概率统计习题(概率的性质、全概率公式)
目录
概率的性质
题一
全概率公式
题二
题三 概率的性质
有限可加性:
若有限个事件互不相容,则 单调性:
互补性:
加法公式: 可分性: 题一 在某城市中共发行三种报纸:甲、乙、丙。在这个…
齐次矩阵的理解深入和在图形学、Unity中的应用
齐次矩阵的理解和在图形学、Unity中的应用
在探讨图形学和Unity中的3D编程时,我们经常会遇到一个非常核心的数学工具——齐次矩阵。这篇文章将一步步深入地探讨齐次矩阵的基本概念、它在图形学中的应用,以及如何在Unity中利用这一概念来创建令人震撼的3…
详解矩阵的三角分解A=LU
目录
一. 求解Axb
二. 上三角矩阵分解
三. 下三角矩阵分解
四. 矩阵的三角分解
举例1:矩阵三角分解
举例2:三角分解的限制
举例3:主元和乘法因子均为1
举例4:U为单位阵
小结 一. 求解Axb
我们知道高斯消元法可以对应矩阵…
74.搜索二维矩阵 - 力扣(LeetCode)
题目描述 给你一个满足下述两条属性的 m x n 整数矩阵:
每行中的整数从左到右按非严格递增顺序排列。 每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回…
矩阵和向量如何相乘?
矩阵与向量相乘遵循特定的数学规则,这个过程通常被称为矩阵向量乘法。在进行矩阵向量乘法时,矩阵的列数必须与向量的行数相同。以下是一个具体的例子:
例子: 假设我们有一个矩阵 A 和一个向量 v,其中: 在…
线性代数:矩阵运算(加减、数乘、乘法、幂、除、转置)
目录
加减
数乘 矩阵与矩阵相乘 矩阵的幂
矩阵转置
方阵的行列式
方阵的行列式,证明:|AB| |A| |B| 加减 数乘 矩阵与矩阵相乘 矩阵的幂 矩阵转置 方阵的行列式 方阵的行列式,证明:|AB| |A| |B|
为什么两个向量的内积等于模长乘夹角?
为什么两个向量的内积等于模长乘夹角? 已知两个向量 a = [ a 1 , a 2 ] a=[a_1,a_2] a=[a1,a2]和 b = [ b 1 , b 2 ] b=[b_1,b_2] b=[b1,b2],他们的内积为 a b = a 1 b 1 + a 2 b 2 ab=a_1b_1+a_2b_2 ab=a1b1+a2b2,看书上的定义该内积的值是一个标量,并且等…
详解矩阵的LDU分解
目录
一. 矩阵分解
二. 解方程
三. 例题说明
四. 矩阵的LDU分解
五. 矩阵三角分解的唯一性 一. 矩阵分解
其实我们可以把一个线性系统(Linear System)看成两个三角系统(Triangular Systems),本文章将解释为什么可…
线性代数:线性方程组
目录
一、线性方程组概念
二、消元法求线性方程组 三、系数阵的秩与线性方程组的解
无解
唯一解
无数解
相关定理 一、线性方程组概念 二、消元法求线性方程组 三、系数阵的秩与线性方程组的解
无解 唯一解 无数解 相关定理
矩阵的正定(positive definite)性质的作用
1. 定义 注意,本文中正定和半正定矩阵不要求是对称或Hermite的。 2. 性质 3. 作用
(1)Axb直接法求解
cholesky实对称正定矩阵求解复共轭对称正定矩阵求解LDL实对称非正定矩阵求解复共轭对称非正定矩阵求解复对称矩阵求解LU实非对称矩阵求解…
杂题——1097: 蛇行矩阵
题目描述 蛇形矩阵是由1开始的自然数依次排列成的一个矩阵上三角形。 输入格式 本题有多组数据,每组数据由一个正整数N组成。(N不大于100) 输出格式 对于每一组数据,输出一个N行的蛇形矩阵。两组输出之间不要额外的空行。矩阵三角…
线性代数:向量组及其线性相关性
目录
向量组
向量组的线性表示
向量组等价
相关定理
向量组的线性相关性
定理 向量组 向量组的线性表示 向量组等价 相关定理 向量组的线性相关性 定理
TikTok矩阵系统的功能展示:深入解析与源代码分享!
今天我来和大家说说TikTok矩阵系统,在当今数字化时代,社交媒体平台已成为人们获取信息、交流思想和娱乐放松的重要渠道,其中,TikTok作为一款全球知名的短视频社交平台,凭借其独特的创意内容和强大的算法推荐系统&#…
正规矩阵(normal matrix)
概述
正规矩阵(Normal matrix)是在线性代数中的一个概念,指的是一个与其共轭转置矩阵可交换的复数方阵。具体来说,设 A A A是一个 n n n \times n nn的复数方阵, A A A被称为是正规的,如果它满足以下条件…
MIT线性代数笔记-第32讲-基变换,图像压缩
目录 32.基变换,图像压缩图像压缩小波基变换 打赏 32.基变换,图像压缩
图像压缩 图像储存 考虑一个灰度图像,假设它的分辨率为 512 ∗ 512 512 * 512 512∗512像素,其中每一个像素记录了所处位置的灰度值( 0 ∼ 255 0…
格密码基础:子格,q-ary垂直格与线性代数
目录
一.写在前面
二.子空间垂直
2.1 理论解释
2.2 举例分析
三. 零空间
3.1 零空间与q-ary垂直格
3.2 零空间与行/列空间
四. 格密码相关 一.写在前面
格密码中的很多基础原语都来自于线性代数的基本概念,比如举几个例子:
格密码中的非满秩格…
【最优化方法】矩阵的二次型
文章目录 矩阵二次型的定义正定性、负定性、半定性和不定性示例 矩阵二次型的定义
矩阵的二次型是一个与矩阵和向量相关的二次多项式。对于一个实数域上的二次型,给定一个 n n nn nn 的对称矩阵 A A A 和一个列向量 x x x( x x x 是一个 n 1 n1 …
NumPy 中级教程——线性代数操作
Python NumPy 中级教程:线性代数操作
NumPy 提供了丰富的线性代数操作功能,包括矩阵乘法、行列式计算、特征值和特征向量等。这些功能使得 NumPy 成为科学计算和数据分析领域的重要工具。在本篇博客中,我们将深入介绍 NumPy 中的线性代数操作…
线性代数——(期末突击)矩阵(上)-概念篇(矩阵的定义、矩阵的运算、特殊矩阵、初等变换)
目录
矩阵的定义
矩阵的运算
相加
相乘
数乘
与单位阵相乘
矩阵的幂
转置
特殊矩阵
数量矩阵
对称矩阵
伴随矩阵
逆矩阵
初等变换 矩阵的定义
由个数排成的m行n列的数表,称为m行n列的矩阵,简称矩阵,记作: 简记为…
【数值分析】逼近,正交多项式
逼近
由离散点(函数表)给出函数关系通常有两种方法:
使用多项式插值 使用多项式插值会带来两个问题:1. 龙格现象2. 数值本身带有误差,使用插值条件来确定函数关系不合理三次样条插值 三次样条插值克服了龙格现象&…
矩阵求逆引理,SMW恒等式
知识储备:四分块矩阵的LDU和UDL分解 https://zhuanlan.zhihu.com/p/448292459?utm_id0 https://blog.csdn.net/qq_37372155/article/details/120014057 如模糊度协方差阵计算
举例:模糊度参数的求解
线性代数:由矩阵 AB=A 可以推出 B=E 吗?
其实,类似的问题在十几年前的各种提问中就出现了,而且,根据 A B A A BA ABA 推出 B E BE BE 有时候也相当 "符合直觉”,但如果追根问底,矩阵 B B B 到底应该是什么样子的,却很少有详细的解答。
…
0203逆矩阵-矩阵及其运算-线性代数
文章目录 一、逆矩阵的定义、性质和求法二、逆矩阵的初步应用结语 一、逆矩阵的定义、性质和求法 定义7 对于 n n n阶矩阵A,如果有一个 n n n阶矩阵B,使 A B B A E ABBAE ABBAE 则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵,简称逆…
【小呆的力学笔记】弹塑性力学的初步认知二:应力应变分析(2)
文章目录 1.4 主应力空间、八面体应力1.5 应变分析1.6 特殊应力、应变定义 1.4 主应力空间、八面体应力
一点的应力状态不论如何变化,其主应力和主方向一致的话,该点的应力状态就是唯一确定的。因此,我们用主应力方向建立一个三维坐标系来描…
线性代数的学习和整理7:各种特殊效果矩阵汇总
目录
1 矩阵
1.1 1维的矩阵
1.2 2维的矩阵
1.3 没有3维的矩阵---3维的是3阶张量
1.4 下面本文总结的都是各种特殊效果矩阵特例
2 方阵: 正方形矩阵
3 单位矩阵
3.1 单位矩阵的定义
3.2 单位矩阵的特性
3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]…
Krylov matrix
Krylov矩阵是一种在数值线性代数中使用的矩阵,尤其是在迭代解法中用于求解线性方程组、特征值问题和其他线性代数问题。它是由俄国数学家阿列克谢尼古拉耶维奇克雷洛夫(Alexei Nikolaevich Krylov)的名字命名的。 Krylov子空间由以下形式的矩…
2023数据结构期中测验-2023秋-计算机+未来网络专业
这里写目录标题 选择题函数题6-1 求链式表的表长6-2 逆序数据建立链表6-3 删除单链表偶数节点6-4 求二叉树高度6-5 先序输出叶结点 选择题
2-1 下述程序段的时间复杂度为( )
for(i0; i<n-1; i)for(j0; j<n-1-i…
线性代数基础概念和在AI中的应用
基本概念
线性代数是数学的一个分支,专注于向量、向量空间(也称为线性空间)、线性变换和矩阵的研究。这些概念在数据科学、人工智能、工程学和物理学等多个领域都有广泛应用。以下是这些基本概念的详细解释和它们在数据处理和AI中的应用。
…
数值代数中的灵敏度分析【条件数】
文章目录 一、条件数二、解线性方程组问题的条件数 在数值分析领域,灵敏度分析是一种用来评估数值模型对输入参数变化的敏感程度的技术。它在许多科学和工程领域中都有广泛的应用,包括金融、工程设计、自然资源管理等。
一、条件数
一个实际问题化为数…
找到矩阵中位于降序15%位置的值
MATLAB实现
clc
clearvars;
matrix randn(10, 10); % 一个示例矩阵
disp(matrix)value find_value_at_15_percent(matrix);
disp([位于降序中15%位置的值为: , num2str(value)]);% 验证
xreshape(matrix,1,100);
ysort(x,descend);
y(1:16)function value_at_15_percent fi…
分块矩阵的定义、计算
目录 一、定义
二、分块矩阵的加减乘法
三、考点 一、定义
分块,顾名思义,将整个矩阵分成几部分,如下图所示
二、分块矩阵的加减乘法 三、考点
分块矩阵的考点不多,一般来说,有一种:
求分块矩阵的转置…
矩阵理论复习(十一)
正交投影矩阵的应用 值域与零空间
证明向量二范数 如何由已知范数构造新的范数 椭圆范数
向量范数的分析性质 向量范数的等价性 在无限维线性空间中,两个向量范数可以是不等价的。 等价性的重要意义:处理向量问题时,可以基于一种范…
工序排序问题--约翰逊法精讲
什么是约翰逊法?约翰逊法是作业排序中的一种排序方法。选出最短加工时间i*,若最短加工时间有多个,任选1个.若i*出现在机床1,它对应的工件先安排加工,否则放在最后安排,安排后划去该工件,重复上两个步骤,直…
MATLAB | 如何用MATLAB绘制这样有气泡感的网络图
今天给大家带来一款用来绘制有气泡感的网络图的工具函数,绘制效果如下: 花里胡哨的,气泡大小代表流入流出数据量综合,不同颜色的气泡代表属于不同类,两个气泡之间有连线代表有数据流动,连线透明度代表流动数…
卡尔曼滤波 - 状态空间模型中的状态方程
卡尔曼滤波 - 状态空间模型中的状态方程
flyfish
状态方程和观测方程统称为状态空间模型
位移 位移Δxxf−x0\text { 位移}\Delta xx_f-x_0位移Δxxf−x0 x0x_0x0 是起始位置 xfx_fxf 是终止位置 在坐标轴里,右边是正,左边是负
面积等于物体…
可做题2(矩阵快速幂,乘法逆元,exgcd)
题目链接:可做题2 (nowcoder.com)
题目描述
若一个数列a满足条件anan-1an-2,n ≥ 3,而a1,a2为任意实数,则我们称这个数列为广义斐波那契数列。 现在请你求出满足条件a1i,a2为区间[l,r]中的整数,且ak mod pm的广义斐波那契数列有…
在markdown中优雅的编写数学公式 - LaTeX
作为经常使用markdown记录的人来说,纯文本操作是最优雅的,所以我们选择用LaTeX来记录数学公式,我们一起来看下常用公式的写法
一般公式
可用直接使用一般的 * / 号直接书写简单一般的公式,\cdot表示点,\neq表示不等…
奇异值分解(SVD)和图像压缩
在本文中,我将尝试解释 SVD 背后的数学及其几何意义,还有它在数据科学中的最常见的用法,图像压缩。 奇异值分解是一种常见的线性代数技术,可以将任意形状的矩阵分解成三个部分的乘积:U、S、V。原矩阵A可以表示为&#…
games101作业1
1.任务
本次作业的任务是完成旋转矩阵和透视投影矩阵(投影转换中的透视矩阵Perspective projection)。
2.渲染前的步骤及细节
我们在此次作业模拟了将三维空间图形经过模型变换、相机变换(View/Camera transformation )、透视…
Kalman滤波(Part-1:信号模型基础)
Kalman Filters
Dynamical Signal Models
一阶高斯-马尔可夫过程(first-order Gauss-Markov process):描述采样点之间(相邻)的相关性: s[n]as[n−1]u[n](1)s[n] as[n-1] u[n] \tag{1} s[n]as[n−1]u[n](1)
其中u[n]u[n]u[n]是高斯白噪声…
webgl-矩阵、旋转、平移、缩放
关键代码
旋转 /* * [ * cosB, -sinB, 0, 0, * sinB, cosB, 0, 0, * 0, 0, 1, 0, * 0, 0, 0, 1 * ] * * 矩阵本该是这个但是由于webgl的矩阵行和列是颠倒的所以我们传入的矩阵也需要倒置 */ rotationMatrix [ cosB, sinB, 0, 0, -sinB, cos…
考研数学一些曲线形状收录
受苦于章鱼兄的题源1000题,发现在二重积分的时候压根不认识一些曲线,挨个搜出来看看他们长什么beyond 有错欢迎指出,本人很菜,公式有的是自己算的,可能会有错,不要当真 万恶的曲线心形线二级目录三级目录心形线
1.ra(1−sin(θ))ra(1-\sin\left(\theta\right))ra(1−sin(θ)…
在proteus中仿真arduino实现矩阵键盘程序
矩阵键盘是可以解决我们端口缺乏的问题,当然,如果我们使用芯片来实现矩阵键盘的输入端口缺乏的问题将更加划算了,本文暂时不使用芯片来解决问题,而使用纯朴的8根线来实现矩阵键盘,目的是使初学者掌握原理。想了解使用芯…
卡尔曼滤波器简介——多维卡尔曼滤波
原文:多维卡尔曼滤波 (kalmanfilter.net)
目录
前言
基本背景
状态外推方程
示例 - 飞机 - 无控制输入
示例 - 带控制输入的飞机
示例 – 坠落物体
状态外推方程维度
线性时不变系统
线性动态系统建模
状态外推方程的推导
状态空间表示形式
示例 - 等速…
特征值与特征向量几何意义
特征值与特征向量几何意义 特征值与特征向量几何意义特征向量的几何意义:特征值和特征向量在几何变换中的应用特征向量是线性不变量特征值和特征向量意义特征值和特征向量的定义如何理解 A x = λ x A x=\lambda x Ax
MATLAB符号运算(七)
目录
1、实验目的:
2、实验内容: 1、实验目的: 1)掌握定义符号对象和创建符号表达式的方法; 2)掌握符号运算基本命令和规则; 3)掌握符号表达式的运算法则以及符号矩阵运算…
numpy.linalg--线性代数基础
numpy.linalg–线性代数基础
NumPy提供了线性代数函数库linalg,该库包含了线性代数所需的所有功能,可以看看下面的说明。
方法注释dot两数组的点积vdot两向量的点积inner两数组的内积determinant数组的行列式matmul两数组的矩阵积inv求矩阵的逆solve求…
【二维矩阵如何存储在一维数组中(行优先和列优先)】
列优先和行优先的性能取决于具体的硬件架构和代码访问模式。在现代计算机中,内存访问的局部性(locality of reference)对性能至关重要。局部性分为两类:时间局部性(temporal locality)和空间局部性(spatial locality)。时间局部性表示最近访问过的数据项很可能在不久的…
判断无穷积分是绝对收敛还是条件收敛---练习题
本篇文章重点讨论一般无穷积敛散性的判别。(即被积函数在所积区间符号不定,既有正的,也有负的) 不论是绝对收敛还是条件收敛,它本身一定是
收敛的。
狄利克雷判别法: 例题: 首先,将…
银行业数字化运营体系(上):渠道触点矩阵建设
数字化运营体系是构建从获客、激活、留存、营收转化到转介的客户全生命周期的运营体系,推动线上产品和业务运营的数字化与智能化。 随着互联网技术的不断发展,移动设备已经成为人们日常生活中不可或缺的一部分,越来越多的用户在数字化渠道进行…
2022年上半年软件设计师下午试题
【试题四】(共15分)
阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。
工程计算中经常要完成多个矩阵相乘的计算任务,对矩阵相乘进行以下说明。
(1)两个矩阵相乘要求第一个矩阵的列数等于第二个…
强化学习:贝尔曼最优公式
策略改进案例 强化学习的目的是寻找最优策略。其中涉及两个核心概念最优状态值和最优策略,和一个工具:贝尔曼最优公式。 首先,我们给出一个熟悉的例子,了解贝尔曼方程是如何改进策略的。 根据给出的策略,我们很容…
numpy 特征值分解
import numpy as np# 搞个矩阵
a np.array([[1,2,3,4],[2,4,5,8],[7,6,5,2],[5,4,3,2]])# 计算a的协方差矩阵
b np.corrcoef(a)# 特征值分解
c np.linalg.eig(b)# d为特征值
d c[0]
# 对角化
g np.diag(d)
# e为特征向量矩阵
e c[1]# 验证特征值分解定义公式
f np.matmu…
高斯消元法解线性方程组
高斯消元法
这种方法,可以在接近O(n3)的复杂度下求解线性方程组,忧郁克拉默法则的O(n*n!)
对于一组线性方程组,枚举每一列进行如下步骤: 1、找到绝对值最大的一行 2、将这一行交换到第一行 3、将这一行的第一个数变成1ÿ…
[坐标系转换]车体坐标系 转 像素坐标系
1.动机
在项目中,我们常常需要绘制无人车激光雷达的BEV图。而原始激光雷达的点所处的坐标是车体局部坐标系(简称为vehiclepose)。所以就涉及到一个坐标系的转换,如图所示,由vehiclepose坐标系(记为O1&…
人工智能数学课高等数学线性微积分数学教程笔记(目录)
前言
本文是对人工智能数学课高等数学线性微积分数学教程的学习笔记。由于之前的文章《人工智能数学课高等数学线性微积分数学教程笔记》篇幅过大,导致打开的时候加载缓慢,也不利于阅读,同时由于CSDN的限制原文已经不可更改,原文…
【线性代数】三、特征值和特征向量
目录一、基本概念和性质矩阵方阵考察特征向量二、矩阵的相似三、矩阵相似对角化四、实对称矩阵和正交矩阵五、题型1.抽象型特征值和特征向量2.两矩阵相似的判别和证明3.求可逆矩阵P使得PAP−1ΛPAP^{-1}\LambdaPAP−1Λ4.实对称矩阵相似对角化一、基本概念和性质
特征向量和特…
每日刷题3——牛客,算术转换和二级指针
更新不易,麻烦多多点赞,欢迎你的提问,感谢你的转发,
最后的最后,关注我,关注我,关注我,你会看到更多有趣的博客哦!!!
喵喵喵,你对我…
22矩阵——向量范数和矩阵范数 : 矩阵范数与向量范数的相容、Numpy计算范数
💖💖感谢各位观看这篇文章,💖💖点赞💖💖、收藏💖💖、你的支持是我前进的动力!💖💖 💖💖感谢你的阅读💖,专栏文章💖持续更新!💖关注不迷路!!💖 矩阵线性代数笔记整理汇总,超全面_ 文章目录 三、矩阵范数与向量范数的相容算子范数矩阵范数…
大数定律与中心极限定理
给大家讲个有趣的故事 明天概统小测哦可惜了 我的智商还停留在小学时代可惜了,我需要努力学习Physice Doctor in FutureChebyshev 不等式 (弱)大数定律 Markov 大数定律 Chebyshev 大数定律 独立同分布大数定律 Bernoulli 大数定律 Khinchin …
形式语言与自动机 下推自动机
下推自动机是啥?: 下面是他的模型: 如何运转?: 下面是标准定义,属实有点复杂: 注意状态转移函数成分极其复杂,要考虑现有状态,要考虑输入符号,还要考虑栈。
…
近世代数2:代数运算
代数运算:定义 M集合 上的一个法则 , 如果对于集合上的每一组有 序对 a,b属于M,总存在唯一的 d属于M,使得aobd 。 那么,这样一个法则 就被成为集合 M上的代数运算。
a,b不一定是数,只要是元素就可以了。甚至可以是2个…
【矩阵论】6. 范数理论——基本概念——向量范数与矩阵范数
6.1 基本概念
6.1.1 向量范数
a. 模长(二范数) Cn中向量X(x1x2⋮xn)的模长为∣X∣(X,X)tr(AHA)∣x1∣2∣x2∣2⋯∣xn∣2C^n中向量 X\left( \begin{matrix} x_1\\x_2\\\vdots\\x_n \end{matrix} \right)的模长为 \vert X\vert\sqrt{(X,X)}\sqrt{tr(A^HA…
(转载)从0开始学matlab(第9天)—第一阶段总结
1.编程实例 下面的例子将向大家介绍如何用 MATLAB 解决问题。 例1 温度转换程序 问题: 设计一个 MATLAB 程序,读取一个华氏温度的输入,输出开尔文温度。 答案: 华氏温度和开尔文温度的转换关系式可在物理学课本中找到。其关系式…
SLAM本质剖析番外-李群李代数的微分和导数
0. 简介
这几个月,博主已经从SLAM算法的使用向着算法的数学推导进行了记录和分享,之前也分享了李群李代数关注核心一文,从现象中解释了李群和李代数表达的含义。但是这还不够,所以这次作者作为SLAM本质剖析的番外,来介…
【线性代数笔记】线性代数知识点总结、概念之间关系总结
矩阵的秩
1. 基础
初等变换不改变矩阵的秩。
阶梯形矩阵非零行的个数即为该矩阵的秩。 r ( A ) r ( A T ) r ( A T A ) r ( A A T ) r(\boldsymbol{A})r(\boldsymbol{A}^{\mathrm{T}})r(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A})r(\boldsymbol{A}\boldsymbol{A}^{\mat…
【数项级数】敛散性判别
阅读本篇之前,建议可以先看一下上一篇文章哦! 【数项级数】无穷个数相加一定是个数吗? 柯西收敛准则判断级数敛散性 基本思想利用柯西收敛准则判断级数是否收敛推论:定理 基本思想
在上一篇文章中,初识数项级数&#…
实对称矩阵必可相似对角化的证明
引理 1: 实对称矩阵的特征值都是实数。
证明:设 A A A 为 n n n 阶实对称阵, λ 0 ∈ C \lambda_0 \in C λ0∈C 是 A A A 的任一特征值, α ( a 1 , a 2 , ⋯ , a n ) T ∈ C n \alpha (a_1, a_2, \cdots, a_n)^T \in C^…
【Games101】-> 计算机图形学
[toc]
【Games101】-> 计算机图形学
!!!为什么计算机图形学和计算机视觉不一样?有何区别?!!! 模型(Model) -> 图像(Image): 计算机图形学(渲染 3D -> 2D) 图像(Image) -…
代码随想录算法训练营15期 Day 2 | 977.有序数组的平方 、209.长度最小的子数组 、59.螺旋矩阵II 、总结
977.有序数组的平方 题目建议: 本题关键在于理解双指针思想 题目链接:力扣 思路一:暴力解算,直接将所有元素变成一个平方,然后进行排序。 class Solution {
public:vector<int> sortedSquares(vector<int&g…
机器学习-weka的数据统计
一、思维导图总结 二、过滤器的代码设计
package com.Sple;import weka.core.Instances;
import weka.core.converters.ConverterUtils;
import weka.filters.Filter;
import weka.filters.unsupervised.attribute.Add;
import weka.filters.unsupervised.attribute.Standardi…
剑指 Offer 12. 矩阵中的路径解题思路
文章目录 题目解题思路 题目
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”…
[Eigen中文文档] 无矩阵求解器
文档总目录
英文原文(Matrix-free solvers)
ConjugateGradient 和 BiCGSTAB 等迭代求解器可以在无矩阵环境中使用。为此,用户必须提供一个继承 EigenBase<> 并实现以下方法的封装类:
Index rows() 和 Index cols():分别返回行数和列…
线性代数Python计算:线性变换
对数域PPP上的向量空间PnP^nPn的线性变换TTT,只要在某个基ϵ1,ϵ2,⋯,ϵn\boldsymbol{\epsilon}_1,\boldsymbol{\epsilon}_2,\cdots,\boldsymbol{\epsilon}_nϵ1,ϵ2,⋯,ϵn下,用α1T(ϵ1),α2T(ϵ2),⋯,αnT(ϵn)\boldsymbol{\alpha}_1T(\boldsym…
【算法】【数组与矩阵模块】矩阵中累加和最大的子矩阵和
目录前言问题介绍解决方案代码编写java语言版本c语言版本c语言版本思考感悟写在最后前言
当前所有算法都使用测试用例运行过,但是不保证100%的测试用例,如果存在问题务必联系批评指正~ 在此感谢左大神让我对算法有了新的感悟认识! 问题介绍 …
线性代数Python计算:向量组的线性表示
判断两个nnn-维向量组A:α1,α2,⋯,αmA:\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_mA:α1,α2,⋯,αm和向量组B:β1,β2,⋯,βlB:\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_lB:β1,β2,⋯,βl之间能否…
线性代数Python计算:消元法与矩阵初等变换
对线性方程组 {a11x1a12x2⋯a1nxnb1a21x1a22x2⋯a2nxnb2⋯⋯⋯am1x1am2x2⋯amnxnbn\begin{cases}a_{11}x_1a_{12}x_2\cdotsa_{1n}x_nb_1\\a_{21}x_1a_{22}x_2\cdotsa_{2n}x_nb_2\\\quad\quad\quad\cdots\quad\cdots\quad\cdots\quad\\a_{m1}x_1a_{m2}x_2\cdotsa_{mn}x_nb_n\end…
线性代数Python计算:矩阵的乘法
设n,m,l∈n,m,l\inn,m,l∈ℕ,PPP为一数域。 ∀A(a11a12⋯a1na21a22⋯a2n⋮⋮⋯⋮am1am2⋯amn)∈Pmn\forall\boldsymbol{A}\begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&\cdots&…
线性代数Python计算:生成初等矩阵
numpy的array对象表示的2维数组行标和列标与数学中矩阵的一致,第一个下标为行标,第二个下标为列标。矩阵元素aija_{ij}aij在array对象A中的访问形式为A[i,j]。需要注意的是,数学中矩阵元素的下标——无论是行标还是列标都是从1开始编排的&a…
线性代数Python计算:自定义代数系统
Python是一个面向对象的程序设计语言,可以用类的定义方式来自定义代数系统:定义类中对象(集合元素)所具有的属性以及对象间的运算。Python为顶层抽象类保留了对应各种运算符的虚方法,我们只需在类的定义中重载所需运算…
线性代数Python计算:Python的布尔代数
设B{0,1}B\{0,1\}B{0,1},定义BBB上的或、与、非运算如下 构成布尔代数(B,∨,∧,)(B,\vee,\wedge,\neg)(B,∨,∧,)。
Python中所有的关系运算结果均为布尔值:非True即False。常用关系运算符罗列如下:
运算符含义(1)<严格小于(2)<小于…
leecode-搜索二维矩阵
题目
题目
分析
不能全if ,得写else if 啊 因为j–会修改j!!!
代码
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int nmatrix.size();//n行int mmatrix[0].size(…
[Eigen中文文档] 扩展/自定义Eigen(二)
文档总目录 本文目录 使用nullary-expressions操作矩阵示例 1:循环矩阵示例 2:索引行和列 使用nullary-expressions操作矩阵
英文原文(Matrix manipulation via nullary-expressions)
CwiseNullaryOp 类的主要目的是定义过程矩阵,例如由On…
线性代数学习笔记(二十七)——线性方程组有解判定
本篇笔记首先讨论如何将线性方程组写成矩阵或向量形式,并给出系数矩阵和增广矩阵的概念;然后通过判断系数矩阵的秩和增广矩阵的秩的关系,讨论方程组有唯一解、有无穷多解还是无解的条件并给出了相关判定;最后总结了通过系数矩阵求…
线性代数学习笔记(二十六)——线性方程组
本篇笔记通过经典的“鸡兔同笼”问题引出了方程组,然后使用消元法对方程组进行求解,并将求解过程与矩阵初等行变换进行对应,最后还将方程组写成了矩阵的形式。
1 方程组引例
为什么会有线性方程组呢?在解决实际问题时会用到方程…
线性代数学习笔记(二十三)——线性相关线性无关
本篇笔记主要围绕向量组的线性表示、线性相关和线性无关介绍相关定理,这些定理在做证明题时会经常用到,需要重点掌握和运用。
1 相关定理
★ 定理3.2.1:向量组α1,α2,...,αs\alpha_1,\alpha_2,...,\alpha_sα1,α2,...,αs线性相关…
使用Cplex求解均值方差模型
在进行多目标进化算法求解投资组合问题时,由于多目标进化算法求得的是一组近似最优解,对于最大化收益和最小化风险的两目标M-V模型,需要找到一个基准,方便作为参考。这里利用Cplex工具求解均值-方差模型。
1、模型构建 马科维茨的…
【数项级数】无穷个数相加一定是个数吗?
数项级数 引入思考问题转化 定义总结重要的例子练习题 引入
思考
数项级数,其实就是要解决无穷个数相加的问题。 而对于无穷求和的问题,思考:无穷个数相加一定是个数吗? 下面,我们来举几个例子: 1 2 2 …
线性代数学习笔记(十五)——初等变换(一)
本篇笔记首先讨论了矩阵的初等变换,包括初等行变换和初等列变换两类,每一类初等变换又有三种变换规则,需要注意该初等变换与行列式对应的性质没有任何关系;然后讨论了初等变换和标准形的关系,任意矩阵都可以通过&#…
线性代数学习笔记(十一)——特殊矩阵
本篇笔记介绍了几种特殊矩阵,包括数量矩阵、对角型矩阵、三角型矩阵、对称矩阵和反对称矩阵,需要注意的是这些特殊矩阵都是方阵。其中对称矩阵和反对称矩阵的两个结论比较重要,在做题时基本都会用到,需要记住。
1 数量矩阵
主对…
线性代数学习笔记(九)——矩阵运算(一)
本篇笔记记录了矩阵的加法和减法、矩阵的数乘和矩阵的乘法运算。需要注意矩阵的加法和减法必须要同型矩阵才行运算;矩阵的数乘是将某数乘以矩阵中的所有元素,与行列式不同,矩阵所有元素均有公因子kkk,该公因子只向外提111次&#…
线性代数学习笔记(七)——克莱姆法则
本篇笔记介绍了用于解方程组的克莱姆法则,该法则只适用于方程个数等于未知量个数的方程组;同时还介绍了齐次线性方程组,并讨论了方程组有零解或有非零解的条件。需要注意的是:克莱姆法则由于计算量比较大,一般不会直接…
线性代数学习笔记(六)——行列式的计算(二)
本篇笔记介绍了三叉型行列式、范德蒙德行列式、反对称行列式和对称行列式。其中三叉型行列式采用加边法求值,范德蒙德行列式通过公式求值,还介绍了范德蒙德行列式公式的证明,以及一些比较隐秘的范德蒙德行列式。对于反对称行列式和对称行列式…
线性代数学习笔记(一)——二阶和三阶行列式
本篇笔记从解方程组开始,并引入一种新运算,然后了解二阶行列式和三阶行列式相关定义,如元素、行标、列标、主对角线、次对角线等。同时为了研究行列式展开项与元素下标之间的关系,还引入了排列、逆序、逆序数、奇排列、偶排列、标…
数论——欧拉函数及欧拉打表
欧拉函数的功能:用于求小于n的与n互质数的个数 欧拉函数的作用:用于求小于n的与n互质数的个数
欧拉函数的公式: φ(n)n*(1-1/p1)(1-1/p2)(1-1/p3)*(1-1/p4)……(1-1/pn), 其中p1, p2……pn为n的所有质因数,n是不为0的整数。φ(1)…
pytorch的数学计算(元素级别)
目录1.绝对值、求和、三角函数2.相乘再相加、相除再相加3.向上取整、向下取整、夹逼函数、乘法、取相反数、取倒数、取平方根倒数和平方根4.除法、余数、取小数、四舍五入、指数运算5.自然对数、平滑对数、幂运算6.线性插值7.Sigmoid函数,sign函数,截断值…
评价算法的优劣标准有什么?
一、评价算法的优劣标准有什么?
1.1什么是算法?
算法就是一个解决问题的方法,一种计算过程。补充:一个程序就是算法与数据结构的组合(数据结构可以直白的理解为研究数据存储的方式)
1.2时间复杂度
想要…
GAMES101笔记 Lecture 01
目录 Overview of Computer Graphics图形学的应用场景Video GamesMoviesAnimationsDesignVisualizationVirtual RealityDigital IllustrationSimulationGraphical User InterfacesTypography 为什么要学习计算机图形学?Fundamental Intellectual Challenges(图形学很…
线性代数Python计算:由无关组表示的向量组线性相关性判断
设向量组B:β1,β2,⋯,βnB:\boldsymbol{\beta}_1,\boldsymbol{\beta}_2,\cdots,\boldsymbol{\beta}_nB:β1,β2,⋯,βn可由线性无关向量组A:α1,α2,⋯,αmA:\boldsymbol{\alpha}_1,\boldsymbol{\alpha}_2,\cdots,\boldsymbol{\alpha}_mA:α1,α2,⋯,αm线性表示 …
线性代数Python计算:Python数系
Python作为计算机程序设计语言,受计算机物理结构的限制,无法表示出完整的整数集合ℤ、有理数集合ℚ、实数集合ℝ及复数集合ℂ。然而,Python所模拟的ℤ、ℚ、ℝ和ℂ在大多数实际应用中可以满足需求。 具体地说,Python中的整数取值范…
短视频矩阵抖音账号矩阵系统源码开发者自研(一)
一、短视频矩阵系统源码框架建模搭建 目录
一、短视频矩阵系统源码框架建模搭建
1.抖音账号矩阵系统功能模型建模
2.短视频账号矩阵系统接口开发规则
二、短视频矩阵系统源码视频剪辑转码处理 短视频矩阵系统是一个多功能的视频内容管理系统,用于创建、剪辑发布…
随机过程——马尔科夫链
Markov过程
已知现在的状态,未来状态与过去的状态无关。 P(X(tn1)≤xn1∣X(t1)x1,...,X(tn)xn)P(X(tn1)≤xn1∣X(tn)xn)P(X(t_{n1})≤x_{n1}|X(t_1)x_1,...,X(t_n)x_n) P(X(t_{n1})≤x_{n1}|X(t_n)x_n)P(X(tn1)≤xn1∣X(t1)x1,...,X(tn)xn)P(X(tn1)…
010、Python数据类型之数字
Python数据类型之数字 https://www.runoob.com/python3/ref-math-lgamma.html 数字类型介绍
Python 数字数据类型用于存储数值。
数字数据类型是不允许改变的,这就意味着如果改变数字数据类型的值,将重新分配内存空间。
Python 支持三种不同的数值类型࿱…
矩阵对角化,SVD分解
文章目录矩阵对角化SVD分解参考链接矩阵对角化
矩阵的相似 设 A\boldsymbol{A}A、 B\boldsymbol{B}B 为两个nnn阶矩阵,若存在可逆矩阵 P\boldsymbol{P}P,使得 P−1APB\boldsymbol{P}^{^{-1}}\boldsymbol{A}\boldsymbol{P}\boldsymbol{B} P−1APB 则称 A…
2023年计算机考研数学一考试大纲
2022年计算机考研数学一考纲对外公布时间在2021年11月30日,2022年考研之前考纲基本使用的是2017年版本的考研数学大纲,预计2023年计算机考研数学一也会继续使用2022年考纲,下文就是2022年计算机考研数学一的考纲详情,可供参考。
…
2023年计算机考研数学考一还是二?考研数学一二三区别
2023年计算机专业考研数学基本是考数学一,除此之外,计算机专业考研科目有英语一、政治和专业课,共计四门,总分是500分,录取分基本在300分以上。
2023年计算机专业考研科目是什么呢?
计算机科学与技术学科采用全国统…
MIT线性代数的总整理
MIT线性代数的总整理 整个线性代数总的来说,可以把线性代数的内容分为几个部分:1)第一部分:线性代数的基本定理,表明四个基本子空间之间的关系,重点是研究维数;(1到13讲)…
【线性代数】快速复习笔记
线性代数快速复习 行列式行列式的基础计算某行(列加上或减去另一行(列的几倍,行列式不变某行列乘k,等于k乘此行列式互换两行列,行列式变号 行列式的性质1 主对角线是X,其余是其他常数a2 范德蒙德行列式3 行列式加减法4…
武忠祥老师每日一题||不定积分基础训练(四)
∫ d x 1 x 3 \int \frac{\rm dx}{1x^3} ∫1x3dx 解法一: 待定系数法: ∫ d x 1 x 3 \int \frac{dx}{1x^3} ∫1x3dx ∫ d x ( 1 x ) ( x 2 − x 1 ) \int \frac{dx}{(1x)(x^2-x1)} ∫(1x)(x2−x1)dx 1 3 ∫ ( 1 x 1 − x 2 x 2 − x …
武忠祥老师每日一题||定积分基础训练(二)
仍是上一节中提到的基本思想 武忠祥老师每日一题||定积分基础训练(一) 在这个题中,M和N可以利用奇偶性判断。 如下: 从上可知, M ∫ − π 2 π 2 1 d x M\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}1\,{\rm d}x M∫−…
CUDA矩阵乘法GEMM优化,从全局内存到共享内存优化的详细流程
在未优化的矩阵乘法CA*B中,a、b和c分别是指向矩阵 A、B 和 C 的全局内存的指针;blockDim.x、blockDim.y、 和TILE_DIM都等于 w。wxw-thread 块中的每个线程计算 C 的tile中的一个元素,row并且col是由特定线程计算的 C 中元素的行和列。该…
个人对傅里叶分析的理解与整理(持续整理中)
一、线性空间 要搞懂傅里叶变换到底从何而来,必须要从线性空间开始。
数学中一个非常重要的概念就是空间,所谓空间其实就是将遵循一定规则的元素放在一块所形成的集合,比如研究的对象是二维的向量即满足维度为二这个规则,那么所有…
【离散数学】复习:近世代数、格与布尔代数
说明:仅用作应试杂碎知识点备忘,不是知识点总结;大部分源自吉大离散真题 先放个梳理: 群
1,2,3元群都只有一个 且都是交换群单位元e的周期为1.群中周期(阶)为1的元素有且仅有一个(就是单位元)任何群只有一个幂等元就是e.群G的平凡子群有两个,{e}和G本身…
基本矩阵F、本质矩阵E、单应矩阵H的关系
前言:
立体视觉几何中有以下问题: 1.已知一幅图像中一点,如何寻找另一幅图像中这个点的对应点(可用光流法、特征点匹配法) 2.已知两幅图像中两点是对应关系,如何求解两相机的相对位置和姿态【R|t】 3.已知…
Eigen和Sophus 用法的详细介绍
一、Eigen
提供了快速的矩阵线性代数运算,矩阵、向量、旋转矩阵、变换矩阵。
Eigen是纯头文件搭建成的库,使用时只需引入Eigen的头文件即可,不需要链接库文件target_link。
#include <Eigen>
CMakeLists.txt需要添加头文件
includ…
Gauss-Seidel迭代法
Gauss-Seidel迭代法 求解线性方程组 (MATLAB) (数值分析作业自编)
代码如下: *将代码分块,很容易理解。 左端是输出项,右端输入自定义项
function [R,k,x] Gauss_Seidel(A,b,error)
% Gauss-Seidel迭代
…
hdf5文件创建(数据集处理):多个txt文件转成hdf5文件
将test文件夹下的多个txt文件转换为一个hdf5文件:
import h5py
import numpy as np
import os
in_path"test/"
out_path"data"
out_file"test.h5"
#创建输出文件夹
if os.path.exists(out_path)False:os.mkdir(out_path)
in_fileos.…
【数学知识拾贝】模式识别所需要的线性代数知识总结
【导语】本科期间只是将线代学了,并且通过做题拿到了一个不错的分数,但是掌握并不牢靠。到了研究生阶段以后,模式识别、机器学习、应用数学等课程都需要大量运用线代进行推导或者证明,线代知识的匮乏让我很吃力,所以借…
抖音SEO账号矩阵系统源码
一、抖音SEO账号矩阵系统源码思路
1. 数据采集与分析
2. 排名算法设计
3. 用户管理模块
4. 内容推荐系统 二、抖音矩阵系统源码功能概述
(1)多平台多账号管理,支持抖音,快手,好看视频,B站,西瓜&#x…
如何在UE4中做出涟漪的效果
涟漪这个效果我相信很多人都尝试实现过,也有各种实现方法。在这里,我实现的方法是使用Custom节点,用算法生成法线。接下来向大家分享一下思路,看一下最终效果图。文末提供了材质球百度云链接。 最终效果图简单地说一下原理&#x…
Python数值线性方程组
介绍
代数方程组的形式为 A11x1A12x2⋯A1nxnb1A21x1A22x2⋯A2nxnb2⋮An1x1An2x2⋯Annxnbn,(1)\begin{array}{c}A_{11} x_{1}A_{12} x_{2}\cdotsA_{1 n} x_{n}b_{1} \\A_{21} x_{1}A_{22} x_{2}\cdotsA_{2 n} x_{n}b_{2} \\\vdots \\A_{n 1} x_{1}A_{n 2} x_{2}\cdotsA_{n n} x…
C++学习日记#7——方程组的直接分解法求解
直接分解得出的LU矩阵与追赶法分解得出的矩阵有较大的区别,直接分解法得出的L矩阵的主对角线元素都为1,而且下三角形元素(除了特殊情况)都非0,U矩阵上三角形没有固定的规律。当分解矩阵时候只能逐一通过LU交替求解。毕竟直接法不像追赶法没有…
C++学习日记#3——追赶法求解系数矩阵为对角占优的三对角线方程组
在一些实际问题中,例如解常微分方程边值问题,解热传导方程以及船体数学放样中建立三次样条函数等,都会要求解系数矩阵为对角占优的三对角线方程组;——《数值分析(第五版)》 即为Axf;
其中,当>1时&…
线性代数与解析几何——Part3 线性空间 线性变换
线性代数与解析几何——Part3 线性空间 & 线性变换 1. 线性空间 1. 数组空间 & 线性关系2. 秩3. 子空间、基与维数4. 一般线性空间5. 同构 2. 线性变换 1. 定义 & 性质2. 矩阵表达3. 矩阵的相似4. 特征值 & 特征向量5. 相似对角化 1. 线性空间
1. 数组空间 …
ArcGIS中实现土地利用转移矩阵
土地利用转移矩阵,就是根据同一地区不同时相的土地覆盖现状的变化关系,求得一个二维矩阵。通过对得到的转移矩阵进行分析,能够得到2个时相,不同的地类之间相互转化的情况,它描述了不同的土地利用的类型在不…
拉格朗日乘数法及KKT条件-通俗理解
拉格朗日乘子法及KKT条件数学理解
1.拉格朗日乘数法的基本思想
在数学最优问题中,拉格朗日乘数法(以数学家约瑟夫路易斯拉格朗日命名)是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件…
线性代数学习笔记(二十)——向量的定义
本篇笔记首先通过举例来说明向量在生活里都是对应着实实在在具体的东西,然后引出向量的定义以及相关概念,如向量、向量的分量、向量的维数、行向量、列向量、零向量、负向量、向量相等、向量加法、向量减法和向量数乘等,最后还总结了向量的运…
线性代数学习笔记(十九)——矩阵的秩(二)
本篇笔记首先介绍了矩阵行满秩、列满秩、满秩和降秩等概念,并讨论了矩阵秩与r阶子式值的关系;然后重点介绍了阶梯形矩阵和行简化阶梯形矩阵,该部分内容非常重要,后续章节和考试经常会用到;同时还讨论了阶梯形矩阵的用处…
线性代数中的正则化(regularization)(zz)
正则化(regularization)在线性代数理论中,不适定问题通常是由一组线性代数方程定义的,而且这组方程组通常来源于有着很大的条件数的不适定反问题。大条件数意味着舍入误差或其它误差会严重地影响问题的结果。反问题有两种形式。最普遍的形式是已知系统和…
求进制(终极解决办法)
假设在n进制下,下面的等式成立,567*456150216,n的值是(D)。
A.9 B.10 C.12 D.18 解法:
1、先凑个位数字
7 * 6 42 42 % ? 6 排除10
按权重展开 (5n2 6n 7) * (4n2 5n 6) 20n…
【排序27:有序矩阵中第 K 小的元素】
【解题思路】 这道题中matrix是n*n的矩阵,求第k小的元素,如果将n*n个数按照大小排序,放在ans[n*n]的一维数组中,那么ans[k-1]即为所求值。
matrix矩阵每行每列都是递增的,那么每行中的第一个数字,都是该行…
SVD求解旋转矩阵(Least-Squares Fitting of Two 3-D Point Sets论文)
引言
本文主要是针对《Least-Squares Fitting of Two 3-D Point Sets》论文SVD求解旋转矩阵中推导过程中使用到的一些线性代数相关的内容做一些说明,具体算法实现不是很复杂,也有很多其他博客可以参考,比如参考中第2条SVD分解求变换矩阵(C版…
【力扣面试】面试题 01.07. 旋转矩阵
【力扣面试】面试题 01.07. 旋转矩阵 文章目录题目解题思路题目 给你一幅由 N N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。 不占用额外内存空间能否做到? 示例 1: 给定 matrix [ [1,2,3], [4,5,6]…
数学杂谈:高维空间向量夹角小记
数学杂谈:高维空间向量夹角小记 1. 问题描述2. n维空间中的均匀向量 1. 2维以及3维空间中的特殊情况 1. 2维空间中的均匀分布向量3. 3维空间中的均匀分布向量 2. n维坐标系中的均匀向量3. 正态分布的巧妙应用 3. n维空间中两向量夹角考察4. 总结 & 思考 1. 问题…
2022MATLAB学习笔记01(中南大学科学计算与MATLAB语言)
2022MATLAB学习笔记01内容预览笔记笔记内容为日常上课记录与整理,为图片格式,仅供学习。内容预览
1.1 MATLAB 系统环境 1.2 MATLAB 数组数据 1.3 变量及其操作 1.4 MATLAB 矩阵的表示 1.5 矩阵元素的引用 1.6 MATLAB 基本运算 1.7 字符串处理
笔记 ——…
向量空间 vector space
向量空间表示为 R1,R2,R3,R4,...,Rn\bf{R}^1, \bf{R}^2, \bf{R}^3, \bf{R}^4, ..., \bf{R}^nR1,R2,R3,R4,...,Rn 。 Rn\bf{R}^nRn 表示 nnn 维向量集合所组成的空间,称为二维向量空间。但是,并不是所有集合组成的空间都能称作向量空间,必须满…
《线性代数》 李炯生\查建国\王新茂 中国科学技术大学 第2版 部分习题答案
百度了一圈没有靠谱点的答案,于是便有了这篇博客。 只写了一些自己觉得有价值的习题。 文章目录第一章 多项式1.3 整除性与最大公因式习题3习题101.5 实系数与复系数多项式习题1习题2.(4)习题101.6 整系数与有理系数多项式例1例2习题2习题6习题7习题81.8 对称多项式…
MIT 线性代数(34—35)读书笔记
第三十四讲:左右逆和伪逆 前面我们涉及到的逆(inverse)都是指左、右乘均成立的逆矩阵,即A−1AIAA−1。在这种情况下,mn矩阵A满足m=n=rank(A),也就是满秩方阵。
左逆(left inserve) …
两个状态的马尔可夫链
手动推导如下公式。
证明:
首先将如下矩阵对角化: { 1 − a a b 1 − b } \begin {Bmatrix} 1-a & a \\ b & 1-b \end {Bmatrix} {1−aba1−b}
(1)求如下矩阵的特征值: { 1 − a a b 1 − b } { x 1 x 2 } λ { x 1 x 2 }…
回到未来:使用马尔可夫转移矩阵分析时间序列数据
一、说明 在本文中,我们将研究使用马尔可夫转移矩阵重构时间序列数据如何产生有趣的描述性见解以及用于预测、回溯和收敛分析的优雅方法。在时间上来回走动——就像科幻经典《回到未来》中 Doc 改装的 DeLorean 时间机器一样。 注意:以下各节中的所有方程…
CS231n——机器学习:线性分类器、Nearest Neighbor分类器、SVM分类器、Triplet loss(三元损失函数)
1.线性分类器
线性映射:f(xi,W,b)Wxib
以CIFAR-10为例,xi就是第i个图像的像素信息,每个图像数据都被拉长为一个长度为D 的列向量,大小为[D x 1]。其中大小为[K x D]的矩阵W 和大小为[K x 1]列向量b 为该函数的参数。参数W…
斐波那契1(矩阵快速幂加速递推,斐波那契前n项平方和)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网
Keven 特别喜欢斐波那契数列,已知 fib11fib_11fib11,fib21fib_21fib21,对于 n>3n>3n>3,fibnfibn−2fibn−1fib_{n}fib_{n-2}fib_{n…
矩阵乘法和矩阵快速幂
文章目录摘要矩阵矩阵乘法矩阵快速幂矩阵乘法的应用摘要
本文主要讲解矩阵乘法和矩阵快速幂。内容不难,都是定理,重点是矩阵乘法的应用。
蓝桥杯知识点汇总: https://blog.csdn.net/GD_ONE/article/details/104061907
矩阵 数学上…
线性代数的学习和整理5: 矩阵的加减乘除及其几何意义(未完成,建设ing)
目录
1 矩阵加法
1.1 矩阵加法的定义
1.2 加法的属性
1.2.1 只有同类型,相同n*m的矩阵才可以相加
1.2.1 矩阵加法的可交换律:
1.2.2 矩阵加法的可结合律:
1.3矩阵加法的几何意义
2 矩阵的减法
2.1 矩阵减法定义和原理基本同 矩阵的…
《Graph Representation Learning》笔记 Chapter5
系列文章 《Graph Representation Learning》笔记 Chapter2 《Graph Representation Learning》笔记 Chapter3 《Graph Representation Learning》笔记 Chapter4 目录Permutation invariance and equivarianceNeural Message PassingOverview of the Message Passing Framework…
线性代数的学习和整理4: 求逆矩阵的多种方法汇总
目录 原始问题:如何求逆矩阵?
1 EXCEL里,直接可以用黑盒表内公式 minverse() 数组公式求A-
2 非线性代数方法:解方程组的方法
3 增广矩阵的方法
4 用行列式的方法计算(未验证)
5 A-1/|A|*A* &…
线性代数的学习和整理7:各种特殊效果矩阵特例(草稿-----未完成)
目录
1 矩阵
1.1 1维的矩阵
1.2 2维的矩阵
1.3 没有3维的矩阵---3维的是3阶张量
2 方阵
3 单位矩阵
3.1 单位矩阵的定义
3.2 单位矩阵的特性
3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]
3.4 零矩阵
3.4 看下这个矩阵 [0,1;1,0]
3.5 看下这个矩阵…
leetcode304. 二维区域和检索 - 矩阵不可变(java)
前缀和数组 二维区域和检索 - 矩阵不可变题目描述前缀和代码演示 一维数组前缀和 二维区域和检索 - 矩阵不可变 难度 - 中等 原题链接 - 二维区域和检索 - 矩阵不可变 题目描述 给定一个二维矩阵 matrix,以下类型的多个请求: 计算其子矩形范围内元素的总…
creator中关于旋转所使用的欧拉角和四元数
概念
四元数,欧拉角,变换矩阵,这三者是可以相互转化的,但并不是说变换矩阵等于欧拉角或者变换矩阵等于四元数,欧拉角或者说四元数他们只是旋转数据,而一个矩阵是一个空间坐标系,旋转的数据只是…
抖音短视频seo矩阵系统源代码技术开发方案分享
一、 功能结构设计
1. 视频管理:对于不同平台,不同账号,不同格式,不同内容短视频进行管理,素材分组等,实现多资源数据汇和统一管理
2. 数据挖掘分析:通过数据挖掘和数据分析,提供数…
【考研数学】线性代数第四章 —— 线性方程组(1,基本概念 | 基本定理 | 解的结构)
文章目录 引言一、线性方程组的基本概念与表达形式二、线性方程组解的基本定理三、线性方程组解的结构写在最后 引言
继向量的学习后,一鼓作气,把线性方程组也解决了去。O.O 一、线性方程组的基本概念与表达形式
方程组 称为 n n n 元齐次线性方程组…
VS2019配置Cplex12100
前言
Cplex是IBM公司的一款高性能求解器,它在线性规划、整数规划等多个领域都具有不俗表现,对于运筹专业的学生来说,Cplex是不得不学的“神器”。从本文开始,博主将在此记录Cplex的学习之旅,目测内容有基于Cplex的简单…
[JavaScript]螺旋矩阵
螺旋矩阵描述示例1代码解法一:解法二:描述
给定一个m x n大小的矩阵(m行,n列),按螺旋的顺序返回矩阵中的所有元素。
示例1
输入:
[[1,2,3],[4,5,6],[7,8,9]]
返回值:
[1,2,3,6,9,…
【剑指 Offer 12. 矩阵中的路径】(回溯)
【解题思路】
用回溯的方法,查询board[ ][ ]这个二维数组。
class Solution {public boolean exist(char[][] board, String word) {int m board.length;int n board[0].length;boolean[][] visited new boolean[m][n];for(int i 0; i < m; i){for(int j …
14-矩阵相乘及其运算法则
矩阵与向量的乘法
在这一篇文章中我们就将基于上一篇重新审视矩阵的这个视点来理解矩阵的乘法,那么在这一篇,我们主要来看一下矩阵和向量的乘法。这里这个线性方程组是上一小节给大家举的模拟的一个非常简单的小型经济系统的例子,我们可以把…
线性代数的学习和整理---番外1:EXCEL里角度,弧度,三角函数
目录
1 角的度量:角度和弧度
1.1 角度 angle
1.1.1 定义
1.1.2 公式
1.1.2 角度取值范围
1.2 弧长和弦长
1.3 弧度 rad
1.3.1 弧长和弧度定义的原理
1.3.2 定义
1.3.3 取值范围
1.3.4 取值范围
1.4 角度,弧度的换算
1.5 EXCEL里进行角度和…
高等数学:线性代数-第一章
文章目录 第1章 行列式1.1 全排列和对换1.2 n阶行列式1.3 行列式的性质1.4 行列式按行(列)展开 第1章 行列式
1.1 全排列和对换
全排列 把 n 个不同的元素排成一列,叫做这 n 个元素的全排列,简称排列。
例如, { 5 , 3 , 4 , 2…
深度学习基础知识(三)-线性代数的实现
1.标量使用
标量由只有一个元素的张量表示,标量可以做最简单的计算。
import torch
xtorch.tensor([3.0])
ytorch.tensor([2.0])print(xy)
print(x*y)
print(x/y)
print(x**y)
结果:
tensor([5.])
tensor([6.])
tensor([1.5000])
tensor([9.])
2.向量使用
向…
如何将GPS坐标点如何网格化?
目录
题主问题:
解答:
高效判断点是否在正六边形蜂窝内的方法
代码实现:ArcGIS中实现指定面积蜂窝(正六边形)方法 碰巧自己前段时间处理过类似的数据,讲一下自己的解决思路。
题主问题: 解…
一道关于幂次方矩阵题目的精彩解法
这道题源自23版李林880的矩阵章节,题目如下:
设矩阵 A [ 1 − 1 − 1 − 1 − 1 1 − 1 − 1 − 1 − 1 1 − 1 − 1 − 1 − 1 1 ] A\left[ \begin{matrix} 1 & -1 & -1 & -1 \\ -1 & 1 & -1 & -1 \\ -1 & -1 & 1 &…
lc2536.子矩阵元素加1
暴力解法:直接按照题目所示在矩阵的相应位置加一
时间复杂度:O(n2 * queries.length)
空间复杂度:O(1)
二维差分:创建二维差分数组,通过对差分数组的修改来影响原来的数组,最后还原
时间复杂度&#x…
Leecode螺旋矩阵 II59
59.螺旋矩阵II
题目建议: 本题关键还是在转圈的逻辑,在二分搜索中提到的区间定义,在这里又用上了。
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
文章讲解:代码随想录
视频…
01-向量究竟是什么?
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan 向量究竟是什么 引入一些数作为坐标是一种鲁莽的行为 ——赫尔曼外尔 The introduction of numbers as coordinates is an act of violence - Hermann Weyl 向量的定义 向量࿰…
线性代数复习公式整理(自用/持续更新)
第一章 行列式
设A、B为n阶矩阵 ∣ A T ∣ ∣ A ∣ \left | A^T \right | \left | A \right | AT ∣A∣ ∣ A m ∣ ∣ A ∣ m \left | A^m \right | \left | A \right | ^m ∣Am∣∣A∣m ∣ k A ∣ k n ∣ A ∣ \left | kA \right | k^n\left | A \right | ∣kA∣kn∣A…
Co-Occurrence Matrix——共现矩阵原理介绍
文章目录 共现和上下文窗口共现矩阵的生成共现矩阵存在的问题及解决方法主成分分析 PCA奇异值分解 SVD 共现和上下文窗口
共现(Co-occurrence)——对于给定的语料库,一对单词(如w1和w2)的共现是指它们在上、下文窗口中…
第三章,矩阵,07-用初等变换求逆矩阵、矩阵的LU分解
第三章,矩阵,07-用初等变换求逆矩阵、矩阵的LU分解 一个基本的方法求 A − 1 B A^{-1}B A−1BLU分解例1,求矩阵A的LU分解:例12,LU分解解线性方程组: 玩转线性代数(19)初等矩阵与初等变换的相关应用的笔记&a…
TEC2083BS-PD码转换器(解决博世矩阵控制PELCO派尔高球机的问题)
TEC2083BS-PD码转换器 使用说明
1.设备概述 控制码转换器在安防工程中起着非常重要的角色,随着高速球型摄像机在安防工程中大范围的使用,而高速球厂家都因为某些原因很少使用博世、飞利浦的协议。为此,工程商经常会遇到博世协议和PELCO协议之…
8.利用matlab完成 符号微积分和极限 (matlab程序)
1.简述 一、符号微积分
微积分的数值计算方法只能求出以数值表示的近似解,而无法得到以函数形式表示的解析解。在 MATLAB 中,可以通过符号运算获得微积分的解析解。
1. 符号极限
MATLAB 中求函数极限的函数是 limit,可用来求函数在指定点的…
第三章,矩阵,08-矩阵的秩及相关性质
第三章,矩阵,08-矩阵的秩及相关性质 秩的定义1最高阶非零子式定理秩的定义2秩的性质性质1性质2性质3性质4性质5性质6性质7性质8性质9性质10性质11性质12性质12的推论 玩转线性代数(20)矩阵的秩的笔记,相关证明以及例子见原文 秩的定义1
设矩…
数学分析:曲线曲面积分
这一章还是很重要的,可以看到为什么dt1^dt2和dt1dt2是一样的。 可以看到,核心还是黎曼和,我们把两种微分的黎曼和都列出来,并且证明两个相等,即可。
这里要注意,微分形式的积分,在黎曼和的情况…
pytorch的数值比较运算
目录:1. 大于、大于等于、小于、小于等于、不相等2. 最大值,最小值3. 排序4. topk1. 大于、大于等于、小于、小于等于、不相等
# 元素相等返回1,不相等返回0.
x torch.Tensor([[2,3,5],[4,7,9]])
y torch.Tensor([[2,4,5],[4,8,9]])
z to…
微信记录---推荐系统---23/8/14 小总结
推荐系统---23/8/14 小总结 1. ACM推荐系统专题研讨会2.图神经网络推荐系统3.表1 模型效果对标:MovieLens 1M4.爬虫技术5.TF-IDF算法6.图 2 海量学术大数据推荐系统技术架构7.图 4 CADAL 平台推荐系统框架设计8.企业推荐系统发展概述MLR(Mixed Logistic Regression)DIEN(Deep…
open------mv----四象限--line interpolation
MoveLine.py
#直线插补代码
#MoveLine.Move_Line_Interpolation(0,0,5,8,1)
#x00,y00,xe5,ye8,quadrant1
#cnt 0,x01,y00
#cnt 1,x01,y01
#cnt 2,x01,y02
#cnt 3,x02,y02
#cnt 4,x02,y03
#cnt 5,x02,y04
#cnt 6,x03,y04
#cnt 7,x03,y05
#cnt 8,x04,y05
#cnt 9,x04,y06
#cnt 10…
【JS 线性代数算法之向量与矩阵】
线性代数算法 一、向量的加减乘除1. 向量加法2. 向量减法3. 向量数乘4. 向量点积5. 向量叉积 二、矩阵的加减乘除1. 矩阵加法2. 矩阵减法3. 矩阵数乘4. 矩阵乘法 常用数学库 线性代数是数学的一个分支,用于研究线性方程组及其解的性质、向量空间及其变换的性质等。在…
二次型化为标准型——给我一个毁灭世界的”配方法“
化标准型的目的:
1、求正负惯性指数
可用于判断A,B是否合同?
2、特征值与特征向量:
标准型的系数就是矩阵的特征值,若为A实对称矩阵则标准型的系数就是行列式A的值
正交变换矩阵就是经过单位化的特征向量 一、配方…
如何理解“对矩阵进行初等行变换不改变其列向量的线性关系”?
对矩阵A进行初等行变换相当于左乘一个可逆矩阵P。
把A看作是列向量组,若有Ax0,则其中的x就说明了列向量的线性关系: [ α 1 , α 2 , α 3 ] [ x 1 x 2 x 3 ] [ 0 ] \left[ \alpha_1 ,\alpha_2, \alpha_3 \right] \begin{bmatrix} x_1\\ x…
【数理知识】三维空间旋转矩阵的欧拉角表示法,四元数表示法,两者之间的转换,Matlab 代码实现
序号内容1【数理知识】自由度 degree of freedom 及自由度的计算方法2【数理知识】刚体 rigid body 及刚体的运动3【数理知识】刚体基本运动,平动,转动4【数理知识】向量数乘,内积,外积,matlab代码实现5【数理知识】最…
LA@向量组线性相关性
文章目录 向量组线性相关性线性相关线性无关多向量向量组线性相关单向量向量组的线性相关性单位向量向量组线性相关性双向量向量组的线性相关性双向量线性相关的几何意义三向量线性相关的几何意义包含零向量的向量组线性相关概念迁移:线性方程组和线性相关齐次线性方程组和向量…
【ArcGIS微课1000例】0072:如何生成空间权重矩阵
严重声明:本文来自专栏《ArcGIS微课1000例:从点滴到精通》,为CSDN博客专家刘一哥GIS原创,原文及专栏地址为:(https://blog.csdn.net/lucky51222/category_11121281.html),谢绝转载或爬取!!! 文章目录 一、空间权重矩阵工具介绍二、ArcGIS生成空间权重矩阵三、注意事项…
算法- 数学(Java实现)
文章目录剑指 Offer 66. 构建乘积数组剑指 Offer 44. 数字序列中某一位的数字思路:剑指 Offer 66. 构建乘积数组
https://leetcode-cn.com/problems/gou-jian-cheng-ji-shu-zu-lcof/
static class Solution {public int[] constructArr(int[] a) {if (a null || …
线性代数的学习和整理13: 定义域,值域,到达域 和单射,满射,双射,反函数,逆矩阵
目录
1 函数与 向量/矩阵
2 初等数学的函数
2.1 函数
2.2 函数的定义:定义域 →映射→ 值域
3 高等数学里的函数:定义域和陪域/到达域(非值域)的映射关系
3.1 函数
3.2 单射,满射,双射等都是针对…
线性代数的学习和整理16:什么是向量空间?什么是空间?什么是距离?(草稿)
什么是向量空间,向量的张成空间?
说空间,先需要从更复杂的概念入手
2.1 转:插播一个数学里其他概念的辨析:群,环,域,集合,空间的定义(表示不懂,…
一道算法题-搜索二维矩阵
这道题记得在《剑指offer》上有,当时急急忙忙的刷过一次,这次静下心来做,还是有一些新的领悟。
搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到…
五分钟看懂前缀和与差分
一、前言
本文主要简单介绍一下前缀和与差分两个内容,主要讲解前缀和与差分的定义,作用和求法三个方面。
因为我们一般认为差分是前缀和的逆运算,所以往往将此两个内容放在一起学习,固此文也按照该模式讲解。
二、前缀和
定义…
LA@特征值和特征向量的性质
文章目录 方阵特征值和特征向量的性质👺特征值之和特征值之积推论:特征值判定方阵的可逆性 证明小结 导出性质可逆矩阵的特征值性质转置矩阵和特征值矩阵多项式的特征值不同特征值的特征向量线性无关定理推论推广 特征向量线性组合特征值的重数性质 方阵特征值和特征…
【线性代数/机器学习】矩阵的奇异值与奇异值分解(SVD)
文章目录 一、引言二、奇异值三、奇异值分解的定义四、如何进行奇异值分解参考资料 一、引言
我们知道,对于一个 n n n\times n nn的矩阵 A A A,如果 A A A有 n n n个线性无关的特征向量,则 A A A可以相似对角化,即存在可逆矩阵…
【线性代数】矩阵求导的本质与分子布局、分母布局的本质(矩阵求导——本质篇)
矩阵求导的本质与分子布局、分母布局的本质(矩阵求导——本质篇) 说在前面一. 函数与标量、向量、矩阵二. 矩阵求导的本质三. 矩阵求导结果的布局四. 分子布局、分母布局的本质五. 向量变元的实值标量函数 说在前面 我将严谨地说明矩阵求导的本质与分子布…
PTA:三元组顺序表表示的稀疏矩阵转置Ⅱ
三元组顺序表表示的稀疏矩阵转置Ⅱ 题目输入格式输出格式输入样例输出样例 代码 题目
三元组顺序表表示的稀疏矩阵转置Ⅱ。设a和b为三元组顺序表变量,分别表示矩阵M和T。要求按照a中三元组的次序进行转置,并将转置后的三元组置入b中恰当的位置。
输入…
线性代数的学习和整理8:行列式相关
目录
1 从2元一次方程组求解说起
1.1 直接用方程组消元法求解
1.2 有没有其他方法呢?有:比如2阶行列式方法
1.3 3阶行列式
2 行列式的定义
2.1 矩阵里的方阵
2.2 行列式定义:返回值为标量的一个函数
2.3 行列式的计算公式
2.4 克拉…
JWFD开源工作流-矩阵引擎-遍历伪代码算法
JWFD开源工作流-矩阵引擎-遍历伪代码算法 XPDL009.MTX 矩阵表
0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 …
判断sparse matrix是否是对称矩阵
参考: https://stackoverflow.com/questions/48798893/error-in-checking-symmetric-sparse-matrix
import scipy.sparse as sp
import numpy as np
np.random.seed(1)a sp.random(5, 5, density0.5)a结果如下
sym_err a - a.T
sym_check_res np.all(np.abs(s…
线性代数的学习和整理21,向量的模,矩阵的模,矩阵的模和行列式比较(未完成)
目录
1 模的定义
2 向量的模是距离
2.1 向量的模的定义
2.2 向量的模的计算公式
3 矩阵的模
3.1 矩阵/向量组的模的定义
3.2 矩阵的模的公式
4 矩阵的模和行列式的关系? 1 模的定义
模,又称为范数。范数,是具有“长度”概念的函数。…
线性代数的学习和整理20,关于向量/矩阵和正交相关,相似矩阵等
目录
1 什么是正交
1.1 正交相关名词
1.2 正交的定义
1.3 正交向量
1.4 正交基
1.5 正交矩阵的特点
1.6 正交矩阵的用处 1 什么是正交
1.1 正交相关名词
orthogonal set 正交向量组正交变换orthogonal matrix 正交矩阵orthogonal basis 正交基orthogonal decompositio…
线性代数的本质(四)——行列式
文章目录 行列式二阶行列式 n n n 阶行列式行列式的性质克拉默法则行列式的几何理解 行列式
二阶行列式
行列式引自对线性方程组的求解。考虑两个方程的二元线性方程组 { a 11 x 1 a 12 x 2 b 1 a 21 x 1 a 22 x 2 b 2 \begin{cases} a_{11}x_1a_{12}x_2b_1 \\ a_{21}x_…
线性代数的本质(一)——向量空间
文章目录 向量空间向量及其性质基与维数向量的坐标运算 《线性代数的本质》 - 3blue1brown 高中数学A版选修4-2 矩阵与变换 《线性代数及其应用》(第五版) 《高等代数简明教程》- 蓝以中 向量空间 In the beginning Grant created the space. And Grant said, Let there be vec…
《Data Cleansing for Models Trained with SGD》笔记
[1] 在其 appendix B 中证 Lemma 7 时说由于 ( 1 − η s Λ ) I ≺ Z s ≺ ( 1 − η s λ ) I \left(1-\eta_s \Lambda\right) I \prec Z_s \prec\left(1-\eta_s \lambda\right) I (1−ηsΛ)I≺Zs≺(1−ηsλ)I,直接可得 (7) 式,这里对 lemma …
线性代数与编程语言结合 基础
什么是线性代数
线性代数是数学的一个分支,研究向量空间和线性变换的理论与方法。它涉及了向量、矩阵、线性方程组、线性映射等概念与运算规则。线性代数在科学和工程领域中被广泛应用,如物理学、计算机图形学、统计学、电子工程等。它提供了一种强大的…
抖音seo短视频矩阵SaaS源码部署--开源搭建(一)
抖音seo短视频矩阵源码是一种基于短视频平台的软件程序,它可以帮助用户在多个短视频平台上进行短视频营销。短视频矩阵源码包含了多种功能,例如短视频上传、短视频批量管理、短视频数据分析等等。用户可以根据自己的需求,选择不同的功能来实现…
Jordan标准形知识梳理
文章目录 λ-矩阵Smith标准形Jordan标准形零化多项式与最小多项式 λ-矩阵
若矩阵 A ∈ C m , n \mathbf{A} \in \mathbb{C}^{m,n} A∈Cm,n 的元素为 a i , j a_{i,j} ai,j 为关于λ的多项式 a i , j ( λ ) a_{i,j}(λ) ai,j(λ),则称 A \mathbf{A} A为λ-…
[矩阵的乘法运算] m*M = c
另人给的一道题,一时没弄出来,后来看WP,复现一下。
对于矩阵运算 m*M c 求m 的情况。
满秩差1半秩
import os
import secret
import hashlib
from Crypto.Util.number import getPrime
from Crypto.Util.Padding import padLEN 32def xo…
【线性代数】为什么 AA* = |A|E
A A ∗ 矩阵相乘,刚好是行列式展开的定义 AA*矩阵相乘,刚好是行列式展开的定义 AA∗矩阵相乘,刚好是行列式展开的定义 矩阵提取一个因子 ∣ A ∣ ,所有元素需要除 ∣ A ∣ 矩阵提取一个因子 |A|,所有元素需要除 |A| 矩…
线性代数+分治:446E
https://codeforces.com/problemset/problem/446/E
把官方题解翻译了一遍
考虑暴力,肯定想到dp,然后变成矩阵。设用代替 (这样子数之间的差值不会变化,但对于问题的处理能方便很多)
我们先令(也就是初始…
贪心找性质+dp表示+矩阵表示+线段树维护:CF573D
比较套路的题目
首先肯定贪心一波,两个都排序后尽量相连。我一开始猜最多跨1,但其实最多跨2,考虑3个人的情况: 我们发现第3个人没了,所以可以出现跨2的情况
然后直接上dp,由 i − 1 , i − 2 , i − 3 i…
【线性代数】齐次与非齐次线性方程组有解的条件
齐次线性方程组 AX 0 的解 A \bm{A} A 是 m n m \times n mn 矩阵,对其按列分块为 A [ a 1 , a 2 , . . . , a n ] A [\bm{a}_1, \bm{a}_2, ..., \bm{a}_n] A[a1,a2,...,an],则齐次线性方程组 A X 0 \bm{AX} \bm{0} AX0 的向量表达式为&a…
如何实现矩阵的重采样问题
文章目录 前言一、问题描述二、回答 前言
记录知乎的自问自答。
一、问题描述
我的问题是这样的,有两个列向量E和F,需要注意的是,E和F是连续的,可任意插值,得到包含其中的子向量。E和F通过一个mn的矩阵联系起来&…
连续类功放通解2:连续类单管功率放大器底层实现原理
连续类功放通解2:连续类单管功率放大器底层实现原理
本次内容理论性较强,适合对功率放大器理论研究比较感兴趣以及想发论文的小朋友,着重探讨现有的一些带宽拓展模式(也就是连续类)的基本实现原理,并给出其…
关于SSA算法中矩阵的3种运算:转置、求逆、相乘
1、矩阵转置 // 矩阵转置(二维矩阵)public static double[][] transposeTwo(double[][] matrix) {int rows matrix.length;int cols matrix[0].length;double[][] transposedMatrix new double[cols][rows];for (int i 0; i < rows; i) {for (int j 0; j < cols; j)…
矩阵中幸运数(Python)
给你一个 m * n 的矩阵,矩阵中的数字 各不相同 。请你按 任意 顺序返回矩阵中的所有幸运数。幸运数 是指矩阵中满足同时下列两个条件的元素:在同一行的所有元素中最小 在同一列的所有元素中最大 示例 1:输入:matrix [[3,7,8],[9,…
PyTorch 深度学习之处理多维特征的输入Multiple Dimension Input(六)
1.Multiple Dimension Logistic Regression Model 1.1 Mini-Batch (N samples) 8D->1D 8D->2D 8D->6D 1.2 Neural Network 学习能力太好也不行(学习到的是数据集中的噪声),最好的是要泛化能力,超参数尝试
Example, Arti…
计算机保研推免面试复习大纲(数学+408)
目录 线性代数概率论高等数学信号与系统离散数学操作系统计算机网络计算机组成数据结构算法编译原理C杂项 线性代数 怎么求逆矩阵 逆矩阵: A A − 1 E AA^{-1}E AA−1E,伴随矩阵: A A ∗ A ∗ A ∣ A ∣ E AA^{*}A^{*}A|A|E AA∗A∗A∣A∣…
04 MIT线性代数-矩阵的LU分解 Factorization into A=LU
目的: 从矩阵的角度理解高斯消元法, 完成LU分解得到ALU
1.矩阵乘积的逆矩阵 Inverse of a product 2.矩阵乘积的转置 Transpose of a product 3.转置矩阵的逆矩阵 Inverse of a transpose 4.矩阵的LU分解 U为上三角阵(Upper triangular matrix), L为下三角阵(Lower triangular…
SEAL:RLWE-BFV 开源算法库
参考文献:
GitHub - microsoft/SEAL: Microsoft SEAL is an easy-to-use and powerful homomorphic encryption library.[HS13] Halevi S, Shoup V. Design and implementation of a homomorphic-encryption library[J]. IBM Research (Manuscript), 2013, 6(12-15…
webGL编程指南 第三章 矩阵平移三角形.translatedTriangle_Matrix
我会持续更新关于wegl的编程指南中的代码。
当前的代码不会使用书中的缩写,每一步都是会展开写。希望能给后来学习的一些帮助
git代码地址 :git 接着 上一节 中 我们使用矩阵进行旋转,这次我们使用矩阵实现位移
<!DOCTYPE html>
<…
线性代数3:矢量方程
一、前言 欢迎回到系列文章的第三篇文章,内容是线性代数的基础知识,线性代数是机器学习背后的基础数学。在我之前的文章中,我介绍了梯队矩阵形式。本文将介绍向量、跨度和线性组合,并将这些新想法与我们已经学到的内容联系起来。本…
向量形式四阶龙格库塔法的仿真细节
摘要 给出了四阶龙格库塔法(ODE4)的向量形式,推导了二阶积分器串联型系统的ODE4更新公式,解释了在使用ODE4仿真高阶系统和带外部输入系统时的各种注意事项,最后给出四阶龙格库塔法只能使用一次的重要结论。
标量和向量…
短视频矩阵系统源码/源头搭建技术交付
一、短视频矩阵系统,短视频矩阵源码技术
1、抖音开放平台申请账号,快手平台申请账号;阿里云混剪接口。
2、系统总台支持OEM代理,可以按点数管理。
3、代理功能。包括是否允许再次开二级代理、是否允许OEM等。
4、可支持一条龙…
【数据结构】数组和字符串(三):特殊矩阵的压缩存储:三角矩阵、对称矩阵——一维数组
文章目录 4.2.1 矩阵的数组表示4.2.2 特殊矩阵的压缩存储a. 对角矩阵的压缩存储b. 三角矩阵的压缩存储结构体初始化元素设置元素获取打印矩阵主函数输出结果代码整合 c. 对称矩阵的压缩存储元素设置元素获取主函数输出结果代码整合 4.2.1 矩阵的数组表示
【数据结构】数组和字…
第四章,向量组,2-矩阵等价与向量组等价的关系
第四章,向量组,2-矩阵等价与向量组等价的关系 矩阵乘法与线性表示矩阵等价与向量组等价 玩转线性代数(23)线性组合与线性表示的应用的笔记,相关证明以及例子见原文 矩阵乘法与线性表示
设有 A m ∗ n B n ∗ l C m ∗ l A_{m*n}B_{n*l}C_{m…
数字信号采集保存与处理通用过程
数字信号处理是把信号用数字或符号表示成序列,通过计算机或通用(专用)信号处理设备,用数值计算方法进行各种处理,达到提取有用信息便于应用的目的。例如:滤波、检测、变换、增强、估计、识别、参数提取、频…
2024线性代数复习——矩阵代数
相似矩阵:存在可逆矩阵 P P P,使得 P − 1 A P B P^{-1} A PB P−1APB,则称矩阵 A A A, B B B 相似,特征值相等。注意只有相似矩阵 B B B 是对角阵,我们才说它是可以相似对角化的。 A A A 可以相似对角…
25期代码随想录算法训练营第二天 | 977.有序数组的平方 ,209.长度最小的子数组 ,59.螺旋矩阵II
目录 977.有序数组的平方思路代码 209.长度最小的子数组代码 59.螺旋矩阵II代码 977.有序数组的平方
链接
思路
双指针。
数组平方的最大值就在数组的两端,不是最左边就是最右边。所以我们可以用一左一右两个指针,来获取最大值,再放入到我…
基于ALS算法的推荐系统研究_徐雪东
RMSE计算公式 ALS存在的问题,以及对应的 解决方案 存在的缺点问题:
1.用户兴趣偏移问题:
即用户的兴趣没有考虑到随着时间的变化,而是说不管是什么时间的用户兴趣,权重占比都是一样的,并没有说用户兴趣会…
07 MIT线性代数-求解Ax=0:主变量,特解 pivot variables, special solutions
前面定义了矩阵的列空间和零空间,那么如何求得这些子空间呢?
1. 计算零空间 Nullspace
A的零空间即满足Ax0的所有x构成的向量空间 对于矩阵A进行“行操作”并不会改变Axb的解,因此也不会改变零空间 unchanged
第一步消元: echelon 阶梯型 …
旋转矩阵的一些特性(左乘右乘)的理解记忆方法。
前言——因为之前总是记混旋转的左乘和右乘和其中的一些规则,所以这篇文章的目的是为了更容易地记住旋转的一些特性,所以并没有太多的基础知识介绍。 在看这篇博客之前,你应该已经知道了一件事情就是旋转矩阵的列向量就是旋转后的坐标系的基向…
线性代数 第六章 二次型
一、矩阵表示 称为二次型的秩。只含有变量的平方项,所有混合项系数全是零,称为标准形;平方项的系数为1、-1或0,称为规范形。
二次型的标准形不唯一,可以用不用的坐标变换化二次型为标准形;二次型的规范形唯…
matlab矩阵的输入
一段时间不操作感觉有些模糊;下面复习一下;
矩阵的数字之间用空格分开,每一行以分号结尾;
空格多几个也是可以识别的;
数字也可以用逗号隔开,只要一行的结尾是分号即可;
空格多输入几个是可…
06 逆矩阵、列空间与零空间
逆矩阵、列空间与零空间 多元一次方程组的矩阵形式线性变换(矩阵)的逆线性变换(矩阵)的秩矩阵的列空间矩阵的零空间 这是关于3Blue1Brown
"线性代数的本质"的学习笔记。 多元一次方程组的矩阵形式
对于多元一次方程组…
10 特征向量与特征值
特征向量与特征值 什么是特征向量三维空间的旋转矩阵和线性变换特征向量二维线性变换不一定有特征向量一个特征值可能不止一个特征向量特征基 这是关于3Blue1Brown
"线性代数的本质"的学习笔记。 图1 预备知识 什么是特征向量 图1 特征向量 线性变换过程中ÿ…
线性代数(四)| 解方程 齐次性 非齐次性 扩充问题
文章目录 1 方程解的个数2 解方程步骤2.1 齐次性方程组2.2 非齐次方程组 3 一些扩充问题 系数矩阵 增广矩阵 A m n X B A_{mn}XB AmnXB
1 方程解的个数
m 代表有m个方程 n代表有n个未知数
系数矩阵的秩与增广矩阵的秩不同 无解
若相同 ,如系数矩阵的秩和未知…
机器学习线性代数知识补充
线性代数知识补充 正交矩阵与正交变换方阵特征值与特征向量相似矩阵对角化二次型正定二次型 正交矩阵与正交变换 方阵特征值与特征向量 相似矩阵 对角化 二次型 正定二次型
【已解决】将一个2708行64列的在GPU上的张量z0矩阵保存下来,格式为csv
问题描述 将一个2708行64列的在GPU上的张量z0矩阵保存下来,格式为csv
初步操作
如果 z0 是一个 PyTorch Tensor,你可以使用以下代码将其保存为 CSV 文件:
import torch import pandas as pd# 假设 z0 是一个 PyTorch Tensor,大…
【深度学习】S2 数学基础 P1 线性代数(上)
目录 基本数学对象标量与变量向量矩阵张量降维求和非降维求和累计求和 点积与向量积点积矩阵-向量积矩阵-矩阵乘法 深度学习的三大数学基础 —— 线性代数、微积分、概率论; 自本篇博文以下几遍博文,将对这三大数学基础进行重点提炼。
本节博文将介绍线…
计算机视觉基础:矩阵运算
矩阵及其表示方式
一个矩阵是由行(row)和列(column)组成的一个矩形数组,通常包含数字。我们可以用大写字母(如 A、B)来表示一个矩阵。例如,矩阵 A 可能看起来像这样:
A [ a11 a12 a13 ][ a21 a22 a23 ][ a31 a32 a3…
短视频(批量剪辑+矩阵发布+爆款文案+无人直播)一体化营销工具
每个主题的视频都是有结构的,我们使用超级编导批量剪辑,软件会将脚本结构化,拆分成一个个分镜,我们只需要准备大量的素材就可以了。 比如口播,用超级编导的AI脚本创作功能,很快就能获得大量的脚本文案&…
线性代数的学习和整理23:用EXCEL和python 计算向量/矩阵的:内积/点积,外积/叉积
目录
1 乘法
1.1 标量乘法(中小学乘法)
1.1.1 乘法的定义
1.1.2 乘法符合的规律
1.2 向量乘法
1.2.1 向量:有方向和大小的对象
1.2.2 向量的标量乘法
1.2.3 常见的向量乘法及结果
1.2.4 向量的其他乘法及结果
1.2.5 向量的模长(长度࿰…
原神启动(递推,矩阵)
Part 1. 引子
求有多少 1 ∼ n 1\sim n 1∼n的排列,满足:
进行 k k k轮原神排序后变为升序
具体的,一轮原神排序的定义为:
指针 i i i按 [ 1 , n ) [1,n) [1,n)的顺序正序遍历,如果 a i > a i 1 a_i>a_{i1}…
MIT_线性代数笔记:线性代数常用计算公式
目录 1.矩阵的加法和数乘2.矩阵的乘法3.转置 Transposes 相关运算 1.矩阵的加法和数乘 2.矩阵的乘法
1)标准方法(行乘以列) 矩阵乘法的标准计算方法是通过矩阵 A 第 i 行的行向量和矩阵 B 第 j 列的列向量点积得到 cij。即我们常说的点积,也…
【代码随想录-数组】螺旋矩阵 II
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学习,不断总结,共同进步,活到老学到老导航 檀越剑指大厂系列:全面总结 jav…
151. 反转字符串中的单词
151. 反转字符串中的单词 原题链接:完成情况:解题思路:参考代码:错误经验吸取 原题链接:
151. 反转字符串中的单词
https://leetcode.cn/problems/reverse-words-in-a-string/description/
完成情况: 解…
使用matplotlib 演示矩阵乘法
使用matplotlib 演示矩阵乘法 代码代码解释代码
import numpy as np
import matplotlib.pyplot as pltplt.ion()# 第一个矩阵
w = 50
h = 30
# 第二个矩阵
w1 = 30
h1 = 50colors0
rotation matrix reflection matrix
文章目录 1. rotation matrix1.1 结论 2. reflection matrix2.1 结论 1. rotation matrix
图像逆时针旋转 θ \theta θ的矩阵 Q r o t a t e [ cos θ − sin θ sin θ cos θ ] (1) Q_{rotate}\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\c…
【考研数学】正交变换后如果不是标准型怎么办?| 关于二次型标准化的一些思考
文章目录 引言一、回顾二次型的定义是什么?什么叫标准二次型?怎么化为标准型? 二、思考写在最后 引言
前阵子做了下 20 年真题,问题大大的,现在订正到矩阵的第一个大题,是关于二次型正交变换的。和常规不同…
如何证明特征值的几何重数不超过代数重数
设 λ 0 \lambda_0 λ0 是 A A A 的特征值,则 λ 0 \lambda_0 λ0 的代数重数 ≥ \geq ≥ 几何重数
证明
假设 A A A 的特征值 λ 0 \lambda_0 λ0 对应的特征向量有 q 维,记为 α 1 , . . . , α q \alpha_1, ... , \alpha_q α1,...,…
MIT_线性代数笔记:列空间和零空间
目录 前言子空间综述列空间 Column space零空间(或化零空间)Nullspaceb 值的影响 Other values of b 前言
本节继续研究子空间,特别是矩阵的列空间(column space)和零空间(nullspace)。
子空间…
线性分组码的奇偶校验矩阵均匀性分析
回顾信道编解码知识,我们知道信道编码要求编码具有检纠错能力,作为FEC(forward error correction)前向纠错编码的一类,线性分组码表示校验位与信息位的关系能够线性表示。 在这篇文章中,并不是要讨论信道编…
【MVP矩阵】裁剪空间、NDC空间、屏幕空间
裁剪空间概述
裁剪空间是一个顶点乘以MVP矩阵之后所在的空间,Vertex Shader的输出就是在裁剪空间上(划重点)
NDC空间概述
接上面,由GPU自己做透视除法将顶点转到NDC空间
两者的转换
透视除法将Clip Space顶点的4个分量都除以…
矩阵的条件数及病态方程组的处理
对 A x b Axb Axb,如果A或者b有轻微的变动,会使得求解出的 x x x发生巨变,这种矩阵就是病态的 A x b Axb Axb 真实情况 A ( Δ x x ) Δ b b A(\Delta xx)\Delta bb A(Δxx)Δbb 代入误差的扰动情况 Δ x A − 1 Δ b \Delta xA^{-1}\Delta b ΔxA−1Δb 取范数后有 ∣…
【矩阵论】Chapter 4—特征值和特征向量知识点总结复习
文章目录 1 特征值和特征向量2 对角化3 Schur定理和正规矩阵 1 特征值和特征向量 定义 设 σ \sigma σ为数域 F F F上线性空间 V V V上的一个线性变换,一个非零向量 v ∈ V v\in V v∈V,如果存在一个 λ ∈ F \lambda \in F λ∈F使得 σ ( v ) λ v \…
如何将四元数转换为旋转矩阵
什么是四元数? 四元数是表示物体在三维空间中的方向和旋转的几种数学方法之一。另一种方法是使用基于欧拉角的旋转矩阵,即滚动、俯仰和偏航,就像的封面图片。
通常使用四元数代替欧拉角旋转矩阵,因为“与 旋转矩阵相比 ÿ…
【矩阵】54.螺旋矩阵(顺时针打印矩形元素)
题目
class Solution {public List<Integer> spiralOrder(int[][] matrix) {int m matrix.length, n matrix[0].length;int leftUpM 0, leftUpN 0, rightDownM m - 1, rightDownN n - 1;List<Integer> res new ArrayList<>();while (leftUpM < ri…
矩阵处理—旋转正方形矩阵
与其明天开始,不如现在行动! 文章目录 旋转正方形矩阵1 题目描述2 解决思路3 代码实现 💎总结 旋转正方形矩阵
1 题目描述
有一个n*n的矩阵,现在把整个矩阵顺时针旋转90,如图: 2 解决思路
设置四个指针&…
【线性代数与矩阵论】Jordan型矩阵
Jordan型矩阵
2023年11月3日 #algebra 文章目录 Jordan型矩阵1. 代数重数与几何重数2. Jordan块与Jordan标准型2.1 最小多项式与Jordan标准型2.2 两类重要矩阵 3. 矩阵的Jordan分解3.1 Jordan分解的应用 下链 1. 代数重数与几何重数
在对向量做线性变换时,向量空间…
用相似对角矩阵加速矩阵的幂,以斐波那契数列为例
《用相似对角矩阵加速矩阵的幂,以斐波那契数列为例》
在计算机科学和线性代数领域,矩阵的幂是一个常见而重要的问题。特别是对于大型矩阵,直接计算幂可能会变得十分耗时。然而,通过相似对角矩阵的方法,我们能够以更为…
向量、矩阵、数组、向量空间
在学习机器学习的过程中,会经常遇到向量、矩阵和数组这些概念,并涉及到多维度,造成许多困惑,因此进行一个总结,主要参考了:https://blog.csdn.net/qq_33419476/article/details/105546442。 向量
概念&…
每日一题:Leetcode1314.矩阵区域和
题目描述:
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
i - k < r < i k, j - k < c < j k 且(r, c) 在矩阵内。 示例…
Multi-value PBS
参考文献:
[CIM19] Carpov S, Izabachne M, Mollimard V. New techniques for multi-value input homomorphic evaluation and applications[C]//Topics in Cryptology–CT-RSA 2019: The Cryptographers’ Track at the RSA Conference 2019, San Francisco, CA, …
保研线性代数机器学习基础复习1
1.什么是代数(algebra)?
为了形式化一个概念,构建出有关这个概念的符号以及操作符号的公式。
2.什么是线性代数(linear algebra)?
一项关于向量以及操作向量的公式的研究。
3.举一些向量的例子&#x…
NCCL实现分布式矩阵乘法的CUDA代码
我们以矩阵乘法C=AB,其中A形状为[M,K],B形状为[K,N],C形状为[M,N]举例子,下面的分布式算法我们默认以MPI来切分数据,其中每个进程之前的数据都是私有,进程之间的数据交互使用通信来完成。 A = ( a 0 , 0
学习transformer模型-矩阵乘法;与点积dot product的关系;计算attention
矩阵乘法: 1、当矩阵A的列数(column)等于矩阵B的行数(row)时,A与B可以相乘。 Ankie的评论:一个人是站着的,一个人是躺着的,站着的高度躺着的长度。 在计算attention的时候…
1.5-数组-059. 螺旋矩阵 II★★
59. 螺旋矩阵II ★★ 力扣题目链接,给你一个正整数 n ,生成一个包含 1 到 n 2 n^2 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。1 < n < 20
示例 1: 输入:n 3
输出:[[1,…
OpenGL的MVP矩阵理解
OpenGL的MVP矩阵理解
右手坐标系
右手坐标系与左手坐标系都是三维笛卡尔坐标系,他们唯一的不同在于z轴的方向,如下图,左边是左手坐标系,右边是右手坐标系 OpenGL中一般用的是右手坐标系
1.模型坐标系(Local Space&…
0202矩阵的运算-矩阵及其运算-线性代数
文章目录 一、矩阵的加法二、数与矩阵相乘三、矩阵与矩阵相乘四、矩阵的转置五、方阵的行列式结语 一、矩阵的加法 定义2 设有两个 m n m\times n mn橘子 A ( a i j ) 和 B ( b i j ) A(a_{ij})和B(b_{ij}) A(aij)和B(bij),那么矩阵A与B的和记为AB,规定为 A B ( a 11…
线性代数笔记25--复数矩阵、快速傅里叶变换
1. 复数矩阵
复向量 Z [ z 1 z 2 z 3 z 4 ⋯ ] Z\begin{bmatrix} z_1\\z_2\\z_3\\z_4\\ \cdots \end{bmatrix} Z z1z2z3z4⋯ 复向量的模长 ∣ z ∣ z ‾ ⊤ z [ z ‾ 1 z ‾ 2 z ‾ 3 ] [ z 1 z 2 z 3 ] \lvert z\rvert\overline z^{\top}z \begin{bmatrix…
【线性代数】决定张成空间的最少向量线性无关吗?
答1:
是的,张成空间的最少向量是线性无关的。
在数学中,张成空间(span space)是一个向量空间,它由一组向量通过线性组合(即每个向量乘以一个标量)生成。如果这组向量是线性无关的&…
【leetcode100-020】【矩阵】旋转图像
【题干】
给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
【思路】
怎么还整上小学奥数题了(不是对角翻转水平/垂…
【数值分析】乘幂法,matlab实现
乘幂法
一种求实矩阵 A {A} A 的按模最大的特征值,及其对应的特征向量 x i {x_i} xi 的方法,只能求一个。特别适合于大型稀疏矩阵。 一个矩阵的特征值和特征向量可以通过矩阵不断乘以一个初始向量得到。 每次乘完之后要规范化,防止上溢或…
线性代数 --- 为什么LU分解中L矩阵的行列式一定等于(+-)1?
以下是关于下三角矩阵L的行列式一定等于-1的一些说明 证明:在LU分解中,下三角矩阵L的行列式一定是. 在证明之前,我这里先补充几条关于行列式的性质:
性质1:对于三角矩阵而言,不论是上三角矩阵还是下三角矩…
SVD如何分解矩阵?
奇异值分解(Singular Value Decomposition,简称SVD)是一种将矩阵分解为三个矩阵乘积的方法,其用途广泛,包括矩阵压缩、降维、最小二乘问题等。下面我将详细解释SVD分解矩阵 A的过程,并提供一个简单的例子。…
短视频矩阵系统+无人直播源码+视频批量分发----开发实践
核心技术
1. AI自动直播:
智能系统通过丰富可定制的文案库, 拥有有料有趣的灵魂。不仅能自动语音讲解内容,还可以在直播中和用户灵活互动。直播中可将团购商品同话术自动上下架。 2. AI剪辑
可一键智能批量成片,也可跟着模板剪…
Android Matrix (三)矩阵组合和应用变换
在 Android 开发中,Matrix 类不仅提供了 mapPoints 方法来变换点坐标,还提供了多种其他用法,使其成为处理图像和视图变换的强大工具。以下是 Matrix 类的一些关键用法:
1. 变换方法
setTranslate(float dx, float dy): 设置矩阵…
邻接矩阵、可达性矩阵、完全关联矩阵、可达性矩阵的计算
邻接矩阵:很简单,就是两个点有关系就是1,没有关系就是0 可达性矩阵:非常简单,两点之间有路为1,没有路为0 可发行矩阵的计算:有n个元素,初始可达性矩阵为A,那么最终的矩阵…
Halcon计算共生矩阵并导出其灰度值特征cooc_feature_image
Halcon计算共生矩阵并导出其灰度值特征
cooc_feature_image 算子的作用与前面介绍的两个算子相似,不同的是输出形式。使用该算子类似于连续执行gen_cooc_matrix算子和cooc_feature_matrix算子。简言之,该算子用一步操作代替了上文中生成矩阵和输出矩阵这…
线性代数——行列式相关性质
目录 一、行列式与它的转置列行列式相等
二、对换行列式的两行(列),行列式变号 三、行列式某行(列)有公因子k,则k可以提到行列式外
四、行列式中若两行成比例,则行列式为0
五、行列式的某一行…
线性代数的学习和整理23:用EXCEL计算 向量/向量组的点乘 (内积) (建设ing)
目录
前言:EXCEL里的的向量相关计算公式
0.1 EXCEL里相关公式
0.2 先说结论:向量组的点乘公式和 向量组的点乘公式不一样
1 向量的点乘 (内积)
1.1 向量的点乘公式
1.2 EXCEL里向量点乘的计算
编辑
1.3 向量点乘的性质
1.3.1 内积的公式…
线性代数基础【5】特征值和特征向量
第五章 特征值和特征向量
第一节、特征值和特征向量的基本概念
一、特征值和特征向量的理论背景
在一个多项式中,未知数的个数为任意多个,且每一项次数都是2的多项式称为二次型,二次型分为两种类型:即非标准二次型及标准二次型 注意:
①二次型X^T AX为非标准二次型的充分必…
矩阵和矩阵如何相乘?
矩阵与矩阵相乘遵循特定的数学规则。为了相乘,第一个矩阵的列数必须等于第二个矩阵的行数。矩阵乘法的结果是一个新矩阵,其行数等于第一个矩阵的行数,列数等于第二个矩阵的列数。矩阵乘法不满足交换律,即 AB≠BA。
例子ÿ…
矩阵的导数运算(理解分子布局、分母布局)
矩阵的导数运算(理解分子布局、分母布局)
1、分子布局和分母布局
请思考这样一个问题,一个维度为m的向量y对一个标量x的求导,那么结果也是一个m维的向量,那么这个结果向量是行向量,还是列向量呢?
答案是:…
Pdf文件格式解析:stream中的变换矩阵指令 1 0 0 -1 0 841.9 cm
解释1 0 0 -1 0 841.9 cm
在PDF文件中的变换矩阵指令 1 0 0 -1 0 841.9 cm 中,前四个数值 1 0 0 -1 组成了一个2x2的线性变换部分,用于描述旋转和缩放操作,而不涉及平移。这里,1 0 0 -1 的每一个数字都有特定的意义: …
数学矩阵GCD和lCM(详解)
矩阵乘法
知阵乘法是《线性代数》中的基础内容,但在考察数学的算法题中也会出现。 本节我们学习基础的矩阵乘法规则。 每个矩阵会有一个行数和一个列数,只有当相乘的两个矩阵的左矩阵的列数等于右矩阵的行数 时,才能相乘,否则不允…
Python---Numpy线性代数
1.数组和矩阵操作: 创建数组和矩阵:np.array, np.matrix 基本的数组操作:形状修改、大小调整、转置等
import numpy as np# 创建一个 2x3 的数组
A np.array([[1, 2, 3], [4, 5, 6]])
print("数组 A:\n", A)# 将数组 A 转换为矩阵…
0205矩阵分块法-矩阵及其运算-线性代数
文章目录 1 分块矩阵的定义2 分块矩阵的运算(性质)3 按列分块与按行分块 结语 1 分块矩阵的定义 将矩阵A用若干条纵线和横线分成许多个小矩阵,每一个小矩阵称为A的子快,以子块为元素的形式上的矩阵称为分块矩阵。 2 分块矩阵的运算…
搜索二维矩阵2 合并两个有序链表
240. 搜索二维矩阵 II - 力扣(LeetCode) class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int i matrix.size() - 1, j 0;while(i > 0 && j < matrix[0].size()){if(matrix[i][j…
面试算法-151-矩阵置零
题目
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1:
输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
解
class Solutio…
矩阵A的转置乘A是否一定正定?矩阵A的转置乘A是正定矩阵的充分必要条件
先上结论: 若矩阵 A ∈ R m n A\in \mathbb{R}^{m\times n} A∈Rmn(可以不要求 A A A是方阵),则对于任意非零向量 x ∈ R n x\in \mathbb{R}^{n} x∈Rn,始终有 x T A T A ≥ 0. x^{\mathsf{T}}A^{\mathsf{T}}A\ge0. …
完全平方数(蓝桥杯,acwing,数论)
题目描述:
一个整数 a 是一个完全平方数,是指它是某一个整数的平方,即存在一个整数 b,使得 ab^2。
给定一个正整数 n,请找到最小的正整数 x,使得它们的乘积是一个完全平方数。
输入格式:
输…
【数据结构】稀疏矩阵的快速转置
【数据结构】稀疏矩阵的转置(普通转置 和 快速转置) 目录 【数据结构】稀疏矩阵的转置(普通转置 和 快速转置)三元表稀疏矩阵的转置方法一(普通转置)复杂度为O(T.muT.nu)方法二:快速转置 复杂度…
切换不会黑屏的矩阵解决方案:旭东泰eKL HDMI KVM矩阵无缝切换器WF404H
随着工作场所的数字化转型和统一集中管理需求的增加,极度需要一种高效而便捷的办公解决方案。4进4出HDMI KVM矩阵无缝切换器是一种功能强大的切换设备,可以让用户通过1套键鼠、4台显示器轻松管理4台电脑主机,并在它们之间进行无缝切换、拼接显…
Armadillo库:用于线性代数和科学计算的快速C/C++库下载及vs环境下的使用方法
armadillo库的下载及使用 一. armadillo库的下载二. vs2022环境下armadillo库的基本使用方法 一. armadillo库的下载
armadillo库的官方下载连接: https://arma.sourceforge.net/download.html
选择网页中最新版本的armadillo库压缩包文件进行下载。 解压armadillo-12.8.2.ta…
<Halcon> 变换矩阵求解
变换矩阵求解
hom_mat2d_translate( : : HomMat2D, Tx, Ty : HomMat2DTranslate) hom_mat2d_translate通过向量t (Tx,Ty)向齐次二维变换矩阵HomMat2D添加平移,得到平移矩阵;vector_to_rigid( : : Px, Py, Qx, Qy : HomMat2D) vector_to_rigid近似于刚性…
18、矩阵-矩阵置零
题解:这道题不能直接双层遍历遇到0就开始行列置零,会影响下次循环遍历。所以可以通过两个集合来记录0所在的行和列,然后再双层遍历遇到标记置0,代码如下:
class Solution {public void setZeroes(int[][] matrix) {if…
【线性代数与矩阵论】矩阵的谱半径与条件数
矩阵的谱半径与条件数
2023年11月18日 文章目录 矩阵的谱半径与条件数1. 矩阵的谱半径2. 谱半径与范数的关系3. 矩阵的条件数下链 1. 矩阵的谱半径
定义 设 A ∈ C n n {A\in \mathbb C^{n \times n} } A∈Cnn , λ 1 , λ 2 , ⋯ , λ n { \lambda_1,\lambda_2…
PyTorch张量运算
诸神缄默不语-个人CSDN博文目录
在深度学习领域,张量是一种非常核心的数据结构,它是标量、向量和矩阵等数学概念的高维扩展。PyTorch作为一款流行的深度学习框架,提供了丰富的张量操作API,帮助研究人员和开发者有效地实现复杂的数…
【DAY05 软考中级备考笔记】线性表,栈和队列,串数组矩阵和广义表
线性表,栈和队列,串数组矩阵和广义表 2月28日 – 天气:阴转晴 时隔好几天没有学习了,今天补上。明天发工资,开心😄 1. 线性表
1.1 线性表的结构
首先线性表的结构分为物理结构和逻辑结构
物理结构按照实…
MongoDB聚合运算符:$covariancePop
$covariancePop聚合运算符返回使用$setWindowFields阶段窗口中的文档计算的两个数值表达式的总体协方差。
$covariancePop运算符只能用于$setWindowFields阶段。
语法
{$covariancePop: {[<numeric expression 1>,<numeric expression 2>]}
}使用
$covariance…
线性代数---------学习总结
线性代数之行列式
行列式的几条重要的性质
1.某两行某两列交换位置之后,值变号
2.行列式转置,值不变
3.范德蒙德行列式,用不同行的公比做一系列的累乘运算
4.把某一行的行列式加到另一行上,利用他们之间的倍数关系࿰…
奠定基础:用于机器学习的微积分、数学和线性代数
一、说明 机器学习是一个引人入胜的领域,它使计算机能够从数据中学习并做出预测或决策,而无需明确编程。然而,在幕后,有一个坚实的数学和线性代数基础,构成了机器学习算法的支柱。在本文中,我们将探讨在深入…
机器人中的数值优化进阶|【一】三次样条曲线推导(上)
机器人中的数值优化进阶|【一】三次样条曲线推导(上)
三次样条曲线的定义
在三次样条曲线中,样条曲线通过一系列控制点 η = [ η 0 , η 1 , . . . η n ] \eta=[\eta_0, \eta_1,...\eta_n] η=[η0,η1,...ηn]来实现对样条曲线的生成。控制点意味着样条曲线必然要…
机器人中的数值优化进阶|【二】三次样条曲线推导(中)
机器人中的数值优化|【自用二】三次样条曲线推导
接之前,由于 c i = 3 ( η i + 1 − η i ) − 2 D i − D i + 1 c_i = 3(\eta_{i+1} - \eta_i) - 2D_i - D_{i+1} ci=3(ηi+1−ηi)−2Di−Di+1 因此有 c = 3 [ − 1 1 0 0 . . . 0 0 − 1 1 0 . . . 0 0 0 − 1…
Nicn的刷题日常之 有序序列判断
目录
1.题目描述
描述
输入描述:
输出描述:
示例1
示例2
示例3
2.解题 1.题目描述 描述 输入一个整数序列,判断是否是有序序列,有序,指序列中的整数从小到大排序或者从大到小排序(相同元素也视为有序)。 数据…
图形学:Transform矩阵(3维 2维) 平移,旋转,缩放
0. 简介
在图形学领域中,Transform矩阵(变换矩阵)是一种表示图形对象在二维或三维空间中的位置、方向和大小变化的数学工具。它们用于执行各种图形变换,如平移、旋转、缩放。Transform矩阵通常表示为一个二维或三维矩阵ÿ…
摆(行列式、杜教筛)
有一个 n n n\times n nn 的矩阵 A A A,满足: A i , j { 1 i j 0 i ̸ j ∧ i ∣ j C otherwise A_{i,j}\begin{cases} 1 &ij\\ 0 &i\notj\land i\mid j\\ C &\text{otherwise} \end{cases} Ai,j⎩ ⎨ ⎧10Cijij∧i∣jotherwi…
BC134 蛇形矩阵
一:题目 二:思路分析
2.1 蛇形矩阵含义
首先,这道题我们要根据这个示例,找到蛇形矩阵是怎么移动的 这是,我们可以标记一下每次移动到方向 我们根据上图可以看出,蛇形矩阵一共有两种方向,橙色…
Rust: 开源线性代数库 nalgebra
在 Rust 中使用 nalgebra 库来处理线性代数问题相对简单。以下是一个基本的示例,展示了如何安装 nalgebra 库、导入它,并使用它来进行一些基础的线性代数运算。
步骤 1: 安装 nalgebra
首先,你需要在你的 Rust 项目中添加 nalgebra 作为依赖…
矩阵乘法--Strassen算法
一、矩阵乘法 从中可以看出,计算两个矩阵的乘积,需要三个 for 循环,可以简单写出代码: for(int i1;i<m;i)for(int j1;j<p;j)for(int k1;k<n;k)c[i][j]a[i][k]*b[k][j];
时间复杂度的分析:很明显,…
线性代数 --- 特征值与特征向量(下)
特征值与特征向量
Eigen Values & Eigen Vectors Part III:如何求解特征向量与特征值
The Key Equation 对于一般矩阵A,如何找到他的特征值与特征向量?
Step I: Find λ first!
首先,我们有方程: 但这里有两个未知数&…
C#,数值计算,数据测试用的对称正定矩阵(Symmetric Positive Definite Matrix)的随机生成算法与源代码
C.Hermite
1、对称矩阵
对称矩阵(Symmetric Matrices)是指以主对角线为对称轴,各元素对应相等的矩阵。在线性代数中,对称矩阵是一个方形矩阵,其转置矩阵和自身相等。1855年,埃米特(C.Hermite,1822-1901年)证明了别的数学家发现的一些矩阵类的特征根的特殊性质,如称为埃…
MATLAB环境下基于可调Q因子小波变换的滚动轴承故障诊断(MATLAB R2021B)
小波变换是一种时频局域化方法,它的窗口面积固定但形状可以发生改变(时间窗与频率窗均可变化)。小波变换在时间域与频率域都能够表示信号的局部特征,并具有多分辨率分析的特点,是机械故障诊断中常用的方法。小波变换故…
C语言——对称矩阵的判定
题目描述:
输入矩阵的行数,再依次输入矩阵的每行元素,判断该矩阵是否为对称矩阵,若矩阵对称输出 yes,不对称输出 no。
输入:
第一行输入一个正整数 N(N≤20),表示矩阵的行数。
下面依次输入…
LC 热题 100:数组与矩阵的探索之旅
LC 热题 100:数组与矩阵的探索之旅
在 LeetCode(力扣)这个编程挑战的宝库中,数组和矩阵是两个经久不衰的主题。它们不仅是数据结构的基础,也是算法问题中常见的元素。今天,我们就来深入探讨一下 LeetCode …
学习AI为啥要掌握高等数学中的线性代数
人工智能为啥要掌握高等数学中的线性代数,这是因为线性代数在人工智能领域扮演着至关重要的角色,其作用体现在以下几个方面:
数据表示: •线性代数中的向量和矩阵是描述和组织数据的重要工具,尤其在机器学习和深度学习…
从相机空间到像素空间的投影和反投影原理和代码
目录
从相机空间到像素空间的投影 效果
编辑 公式
编辑 代码 像素空间到相机空间的反投影 记录一下从相机空间到像素空间的投影(3D-->2D)和像素空间到相机空间的反投影(2D-->3D)。
推荐blog:SLAM入门之视…
灵境矩阵:开启无代码写作新时代,AI智能平台引领创作潮流
灵境矩阵
“灵境杯”智能体创意大赛,瓜分百万超级奖励 在当今数字化快速发展的时代,人工智能(AI)技术正逐渐渗透到我们生活的方方面面。从智能家居到自动驾驶,AI的应用领域不断扩大,而今天,我们…
抖去推无人直播+矩阵托管+AI文案撰写一体化工具如何开发搭建
一、 开发和搭建抖去推无人直播矩阵托管AI文案撰写一体化工具需要以下步骤: 确定功能需求:确定抖去推无人直播、矩阵托管和AI文案撰写的具体功能需求,如直播推流、直播管理、托管服务、AI文案生成等。 技术选型:选择适合开发该工…
短视频矩阵系统源头技术开发--每一次技术迭代
短视频矩阵系统源头开发3年的我们,肯定是需求不断的迭代更新的,目前我们已经迭代了3年之久,写技术文章已经写了短视频矩阵系统,写了3年了,开发了3年了 短视频矩阵获客系统是一种基于短视频平台的获客游戏。短视频矩阵系…
线性代数 - 应该学啥 以及哪些可以交给计算机
AI很热,所以小伙伴们不免要温故知新旧时噩梦 - 线代。 (十几年前,还有一个逼着大家梦回课堂的风口,图形学。) 这个真的不是什么美好的回忆,且不说老师的口音,也不说教材的云山雾绕,单…
2536. 子矩阵元素加 1
跳转题目 本题暴力可以做,猜到用差分,但是不熟,不知道二维差分怎么用,碰到用差分的题目太少了。
暴力算法:
class Solution {
public:vector<vector<int>> rangeAddQueries(int n, vector<vector<…
二维矩阵子集的最大值
登录—专业IT笔试面试备考平台_牛客网
正好遇到了
对于一维,我们只需要贪一次
int ans -1E9;
int suf -1E9;
for (int i 0; i < n; i) {if (i && (a[i] - a[i - 1]) % 2 0) {suf 0;}suf std::max(suf, 0) a[i];ans std::max(ans, suf);
}
ans就是最大值…
【408直通车】(考研数一、二、三合集)线性代数公式全覆盖
线性代数
行列式: ∣ A B ∣ ∣ A ∣ ∣ B ∣ ∣ B ∣ ∣ A ∣ ∣ B A ∣ |AB| |A||B| |B||A| |BA| ∣AB∣∣A∣∣B∣∣B∣∣A∣∣BA∣ ∣ k A ∣ k n ∣ A ∣ |kA| k^n |A| ∣kA∣kn∣A∣ ∣ A T ∣ ∣ A ∣ |A^T| |A| ∣AT∣∣A∣ ∣ A − 1 ∣ ∣ A ∣ −…
小美的平衡矩阵(前缀和例题)
2024美团春招,被这一题给难住了 美团校招笔试真题_Java工程师、C工程师_牛客网
题目: 解答: 这道题的关键点就是要计算出以某一点为矩阵右下角时,1的个数 我一开始是想着遍历,以某一点为起点(矩阵左上角&a…
【蓝桥杯】矩阵快速幂
一.快速幂概述
1.引例
1)题目描述: 求A^B的最后三位数表示的整数,A^B表示:A的B次方。 2)思路:
一般的思路是:求出A的B次幂,再取结果的最后三位数。但是由于计算机能够表示的数字…
【前缀和+双指针】蓝桥杯2022第十三届统计子矩阵
给定一个 N M 的矩阵 A,请你统计有多少个子矩阵 (最小 1 1,最大 N M) 满足子矩阵中所有数的和不超过给定的整数 K?
输入格式:
第一行包含三个整数 N, M 和 K.
之后 N 行每行包含 M 个整数,代表矩阵 A.
输出格式
一个整…
每日一题 第五十七期 洛谷 统计子矩阵
[蓝桥杯 2022 省 B] 统计子矩阵
题目描述
给定一个 N M N \times M NM 的矩阵 A A A,请你统计有多少个子矩阵 (最小 1 1 1 \times 1 11, 最大 N M ) N \times M) NM) 满足子矩阵中所有数的和不超过给定的整数 K K K。
输入格式
第一行包含三个整数 N ,…
保研线性代数机器学习基础复习2
1.什么是群(Group)?
对于一个集合 G 以及集合上的操作 ,如果G G-> G,那么称(G,)为一个群,并且满足如下性质:
封闭性:结合性:中性…
数论与线性代数——整除分块【数论分块】的【运用】【思考】【讲解】【证明(作者自己证的QWQ)】
文章目录 整除分块的思考与运用整除分块的时间复杂度证明 & 分块数量整除分块的公式 & 公式证明公式证明 代码code↓ 整除分块的思考与运用
整除分块是为了解决一个整数求和问题 题目的问题为: ∑ i 1 n ⌊ n i ⌋ \sum_{i1}^{n} \left \lfloor \frac{n}{…
矩阵空间秩1矩阵小世界图
文章目录 1. 矩阵空间2. 微分方程3. 秩为1的矩阵4. 图 1. 矩阵空间
我们以3X3的矩阵空间 M 为例来说明相关情况。目前矩阵空间M中只关心两类计算,矩阵加法和矩阵数乘。
对称矩阵-子空间-有6个3X3的对称矩阵,所以为6维矩阵空间上三角矩阵-子空间-有6个3…
线性代数笔记23--马尔可夫矩阵、傅里叶级数
1. 马尔可夫矩阵
例子 A [ . 1 . 001 . 3 . 2 . 099 . 3 . 7 0 . 4 ] A \begin{bmatrix} .1 & .001 & .3\\ .2 & .099 & .3\\ .7 & 0 & .4 \end{bmatrix} A .1.2.7.001.0990.3.3.4
马尔可夫矩阵满足条件 λ 1 为特征值 \lambda1为特征…
为什么在计算查询Q和键K的矩阵乘法时需要转置键矩阵K。示例说明q11,k11代表什么。线性变换矩阵 W_q 用于生成查询,W_k 用于生成键怎么获取的。
目录
为什么在计算查询Q和键K的矩阵乘法时需要转置键矩阵K。
示例说明q11,k11代表什么。







![[工程数学]1_特征值与特征向量](https://img-blog.csdnimg.cn/51252d63660c480a9a7daa4579f4304e.bmp?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA546L5bSH5Y2r,size_20,color_FFFFFF,t_70,g_se,x_16)
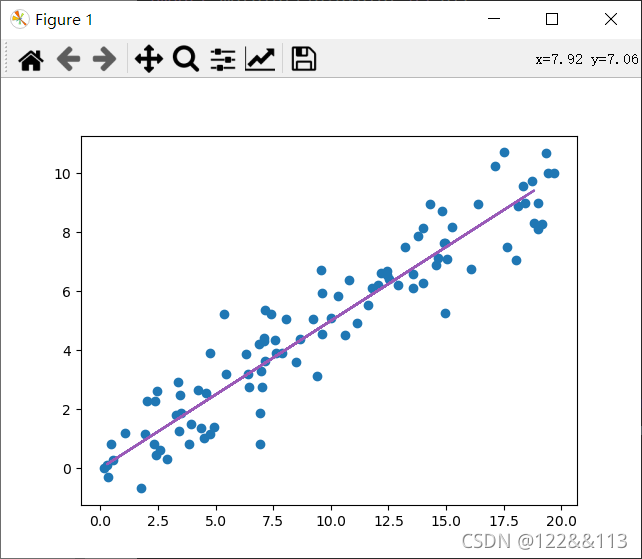
![[解题报告]【第33题】给定一个 n X n 的矩阵,求它的转置矩阵](https://img-blog.csdnimg.cn/d979b132c4614f59b32fe3ed7306965d.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAWGluZ2xlaUdhbw==,size_20,color_FFFFFF,t_70,g_se,x_16)
![[解题报告]【第34题】给定一个 n X n 的矩阵 和 R,求旋转 90R 度以后的矩阵](https://img-blog.csdnimg.cn/661deed7bd2e4026937d92ab6bd2ddb6.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAWGluZ2xlaUdhbw==,size_20,color_FFFFFF,t_70,g_se,x_16)
![[解题报告]《算法零基础100讲》(第1讲) 幂和对数](https://img-blog.csdnimg.cn/822e7a8a5ba24a148fb2c300dc6a6d1b.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAWGluZ2xlaUdhbw==,size_20,color_FFFFFF,t_70,g_se,x_16)









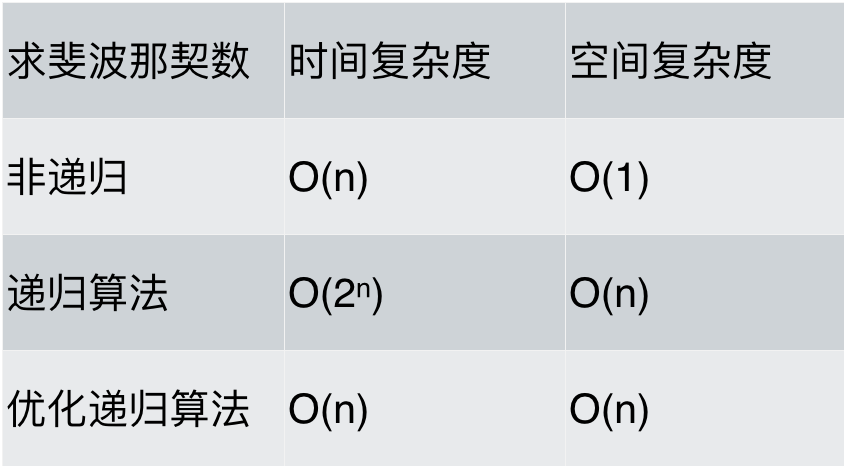



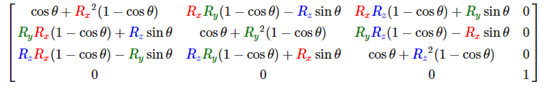


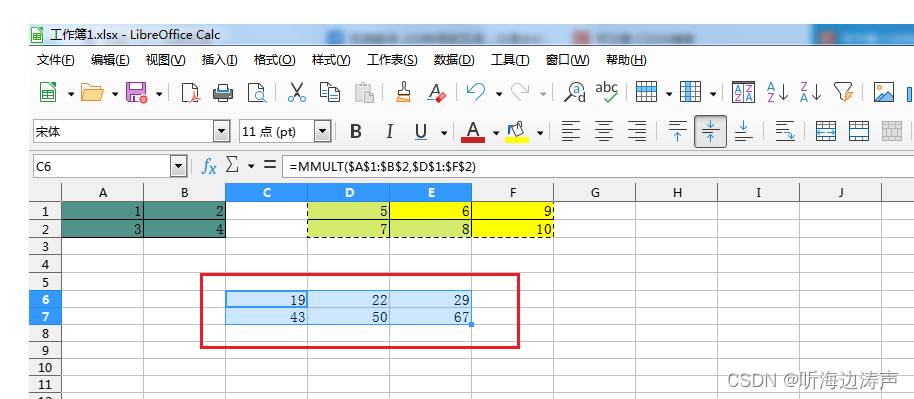
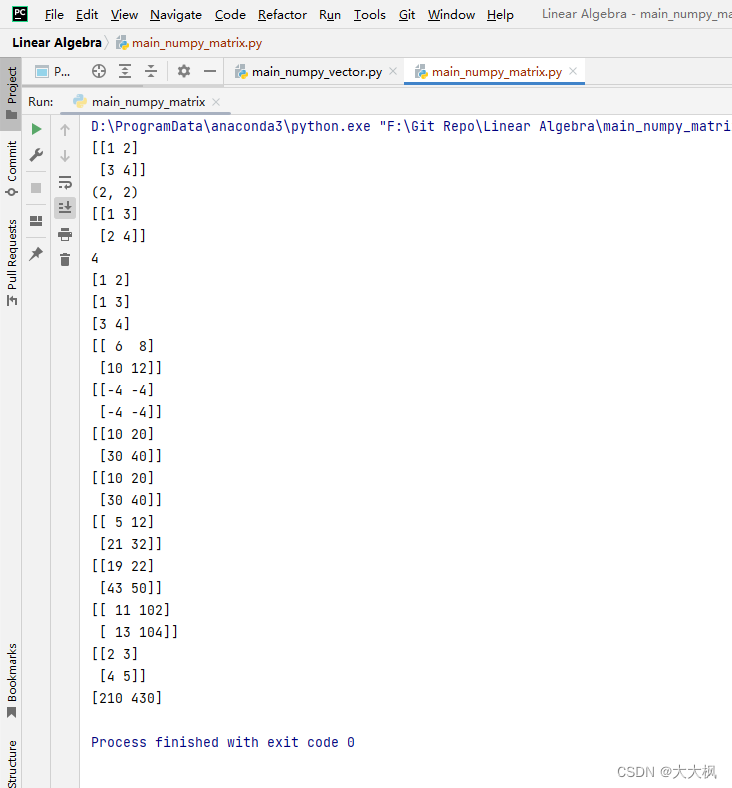
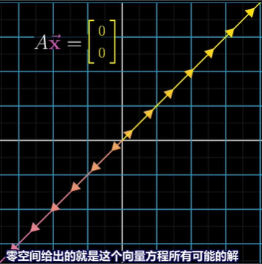


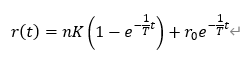

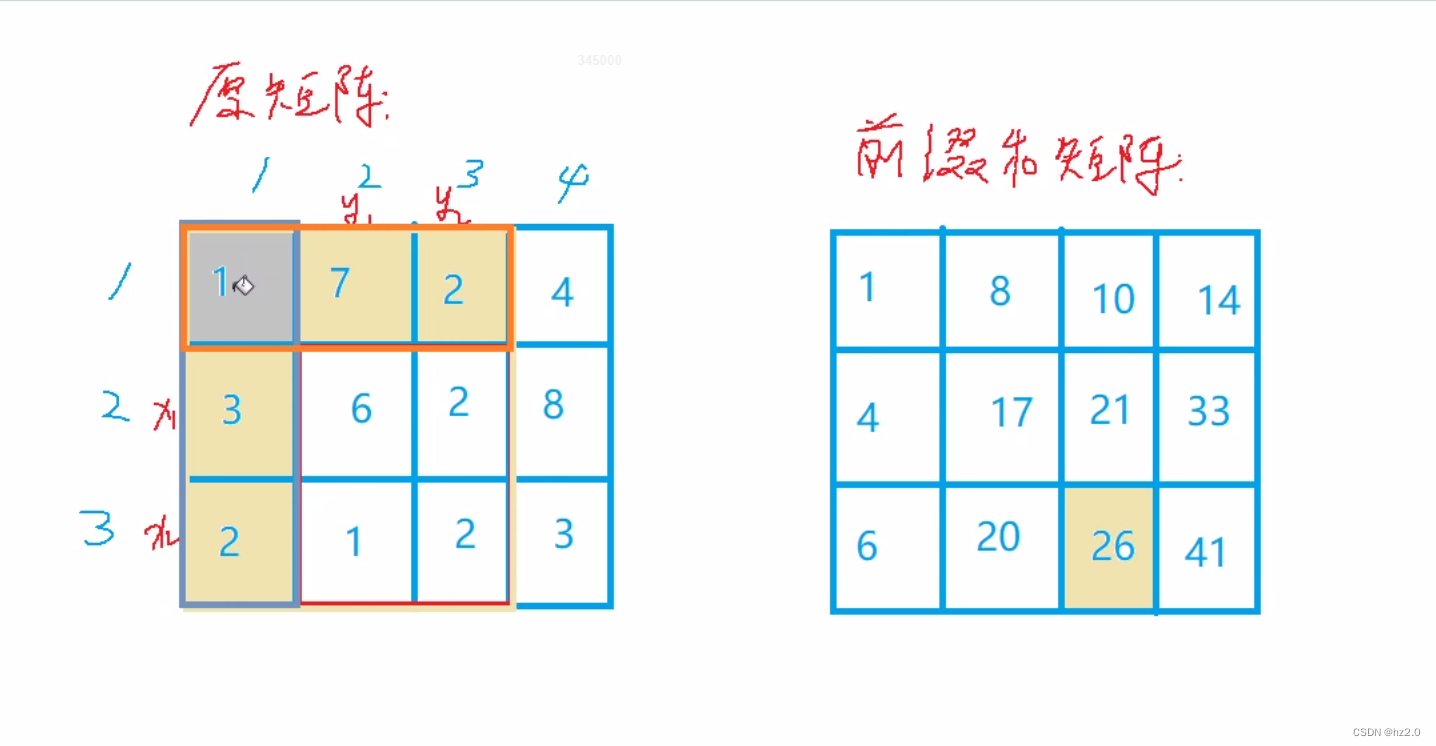

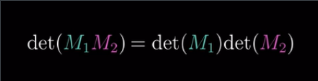
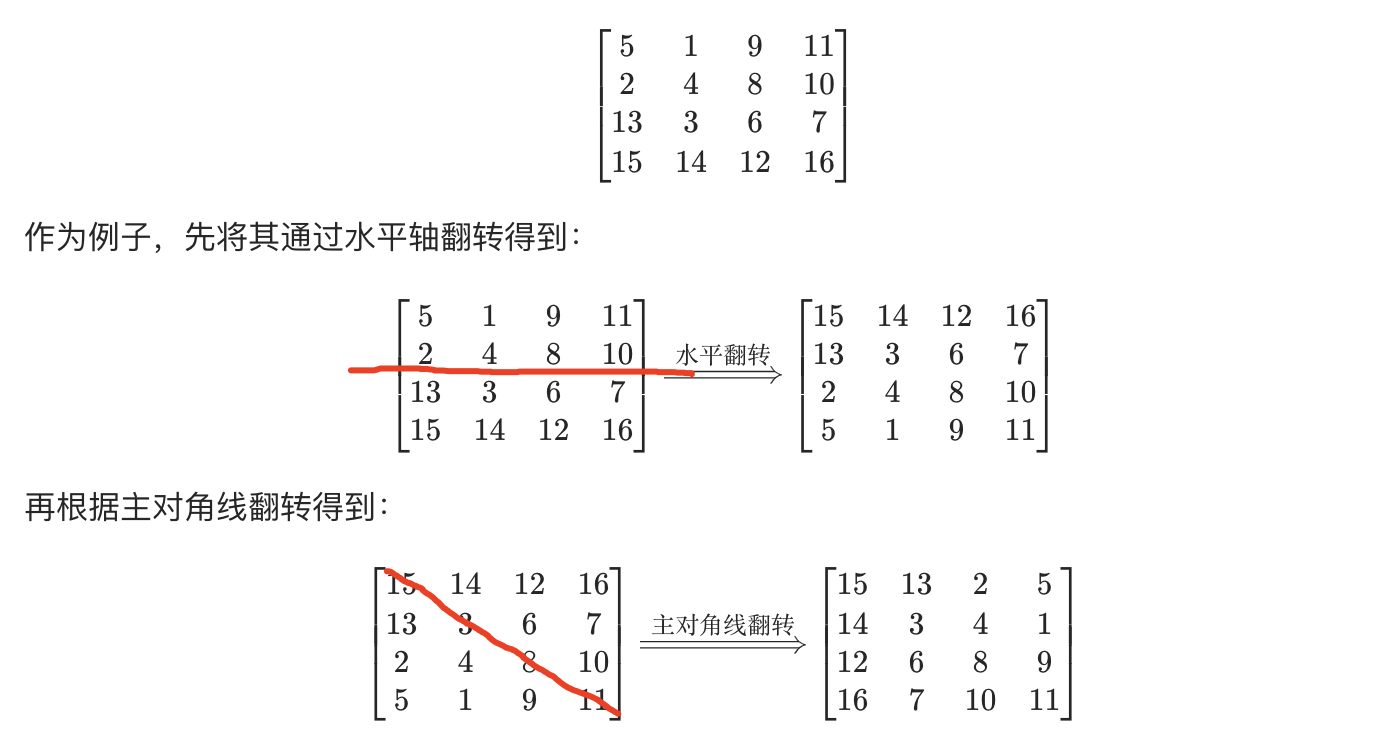

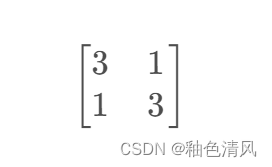
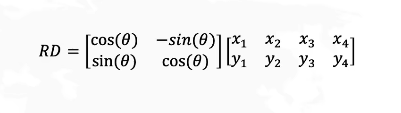
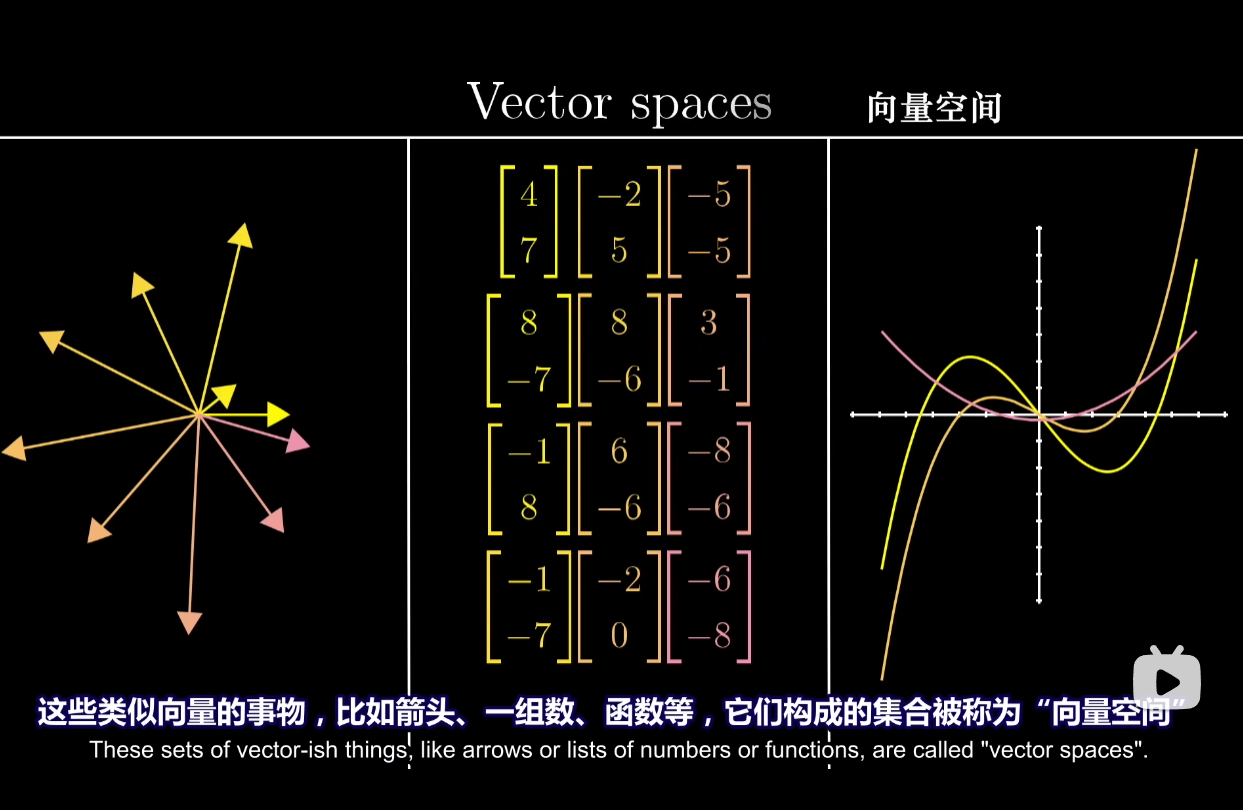
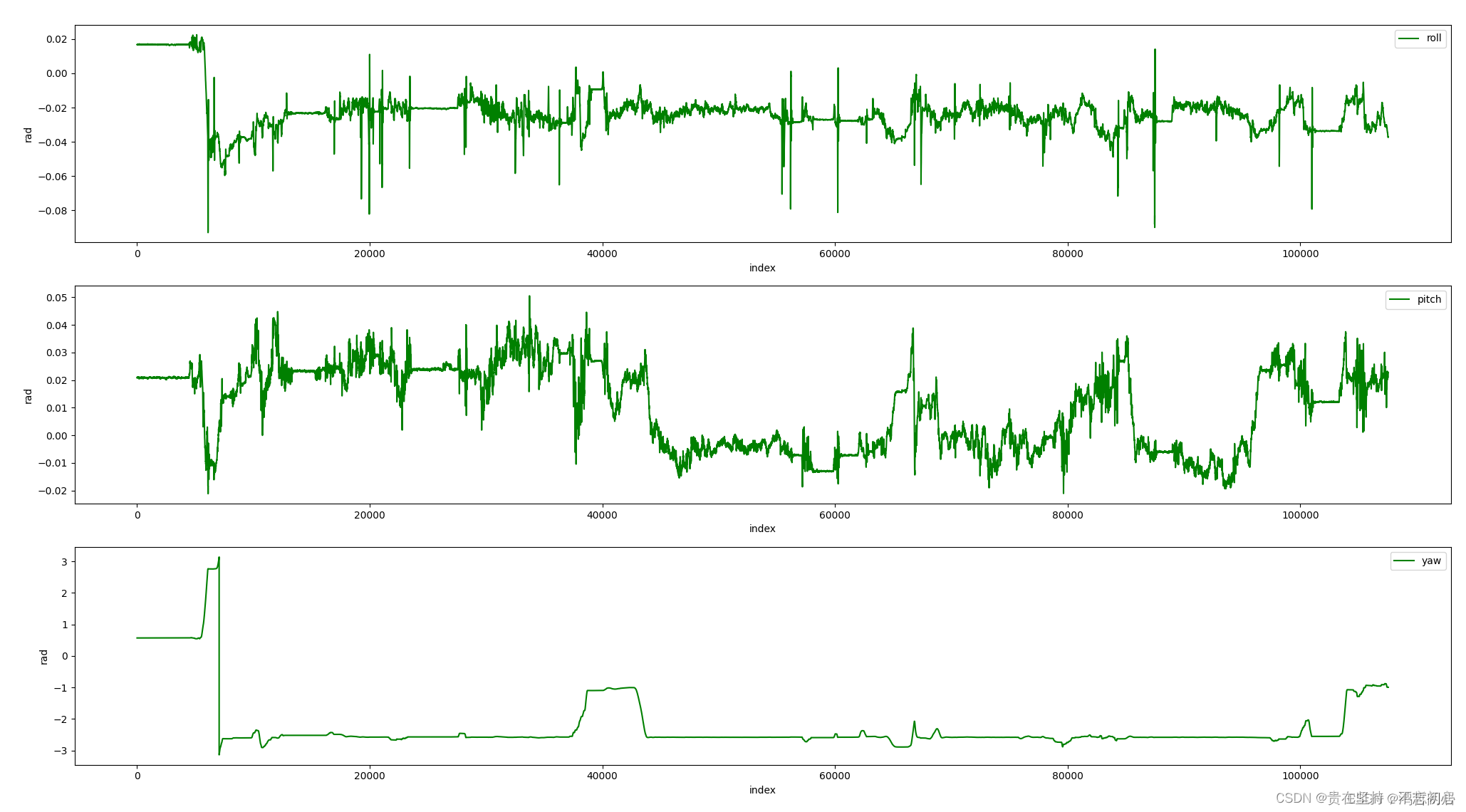
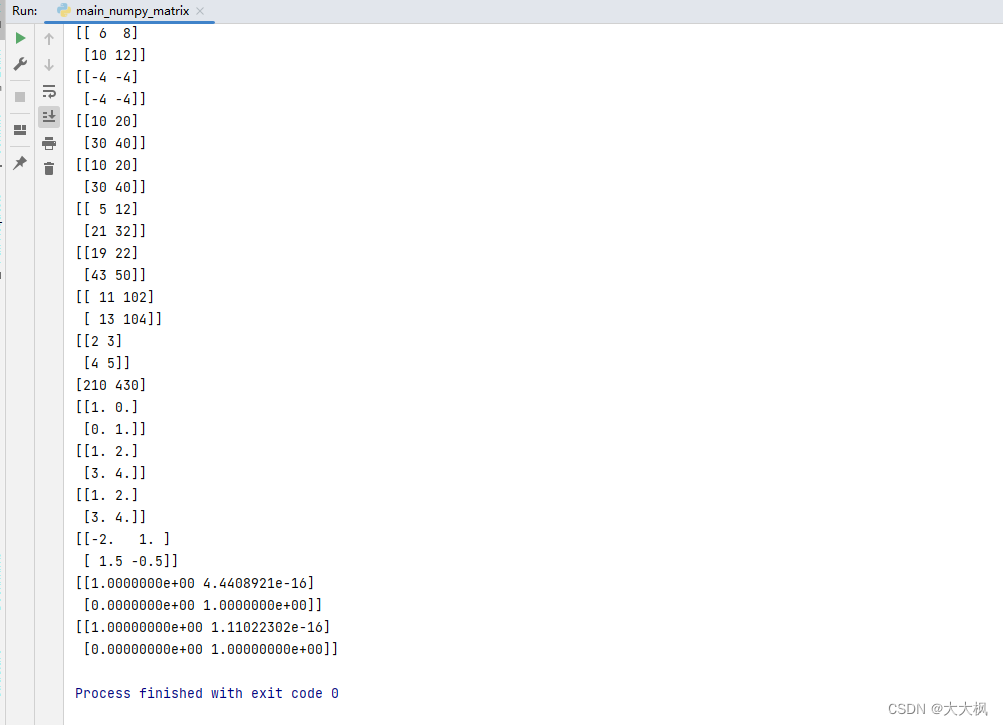

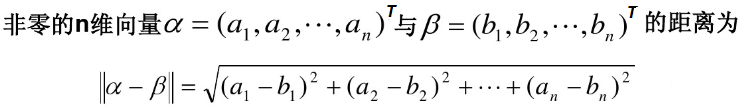
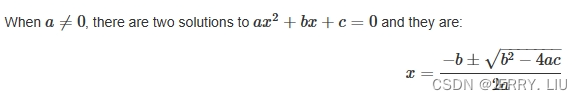








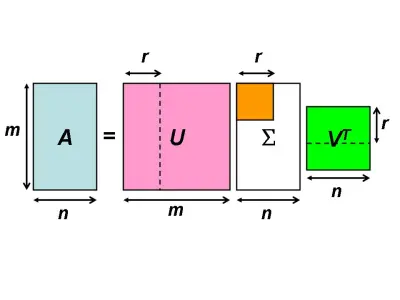
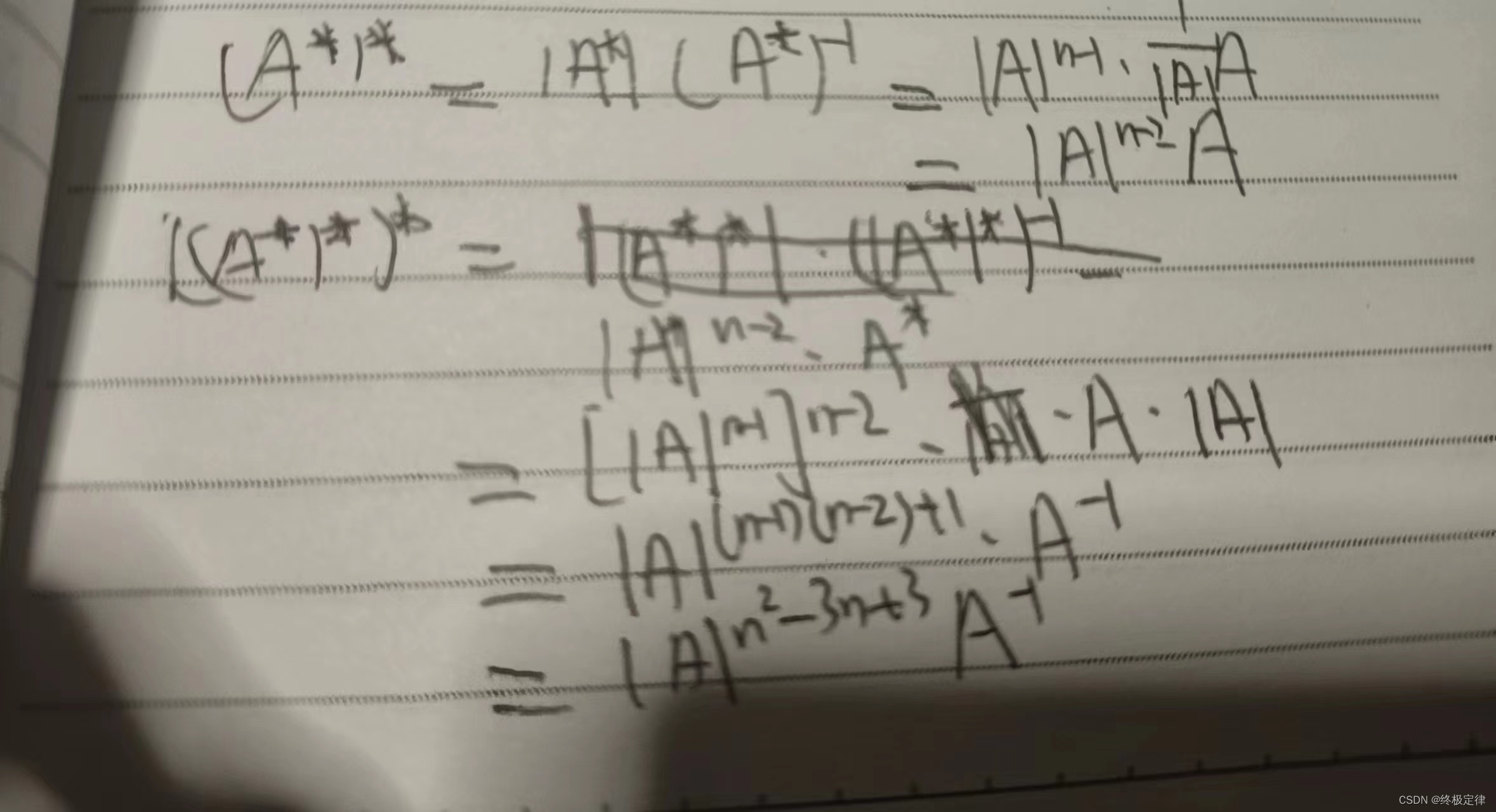
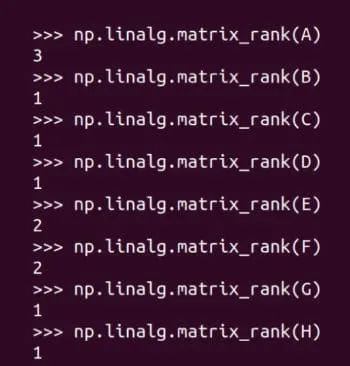
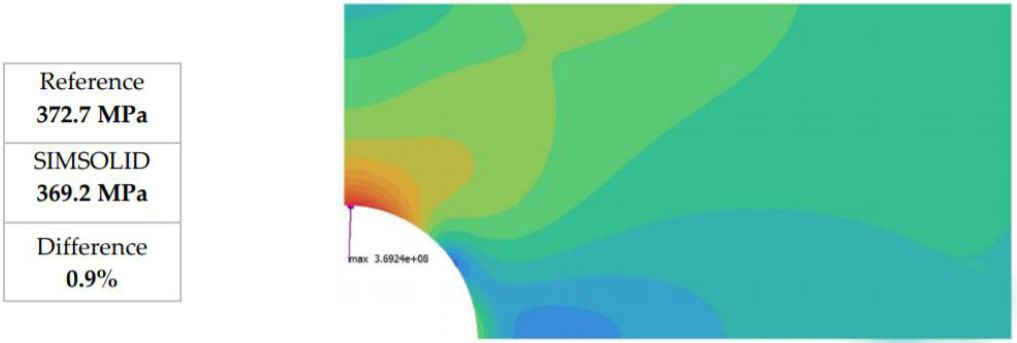


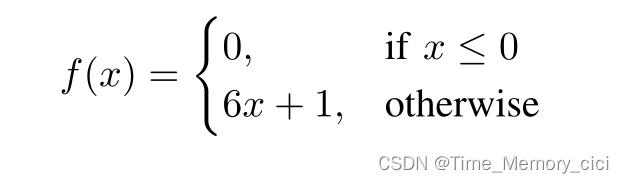













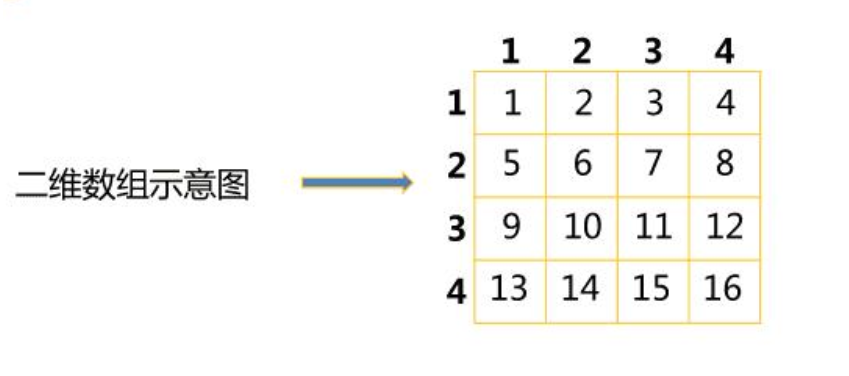

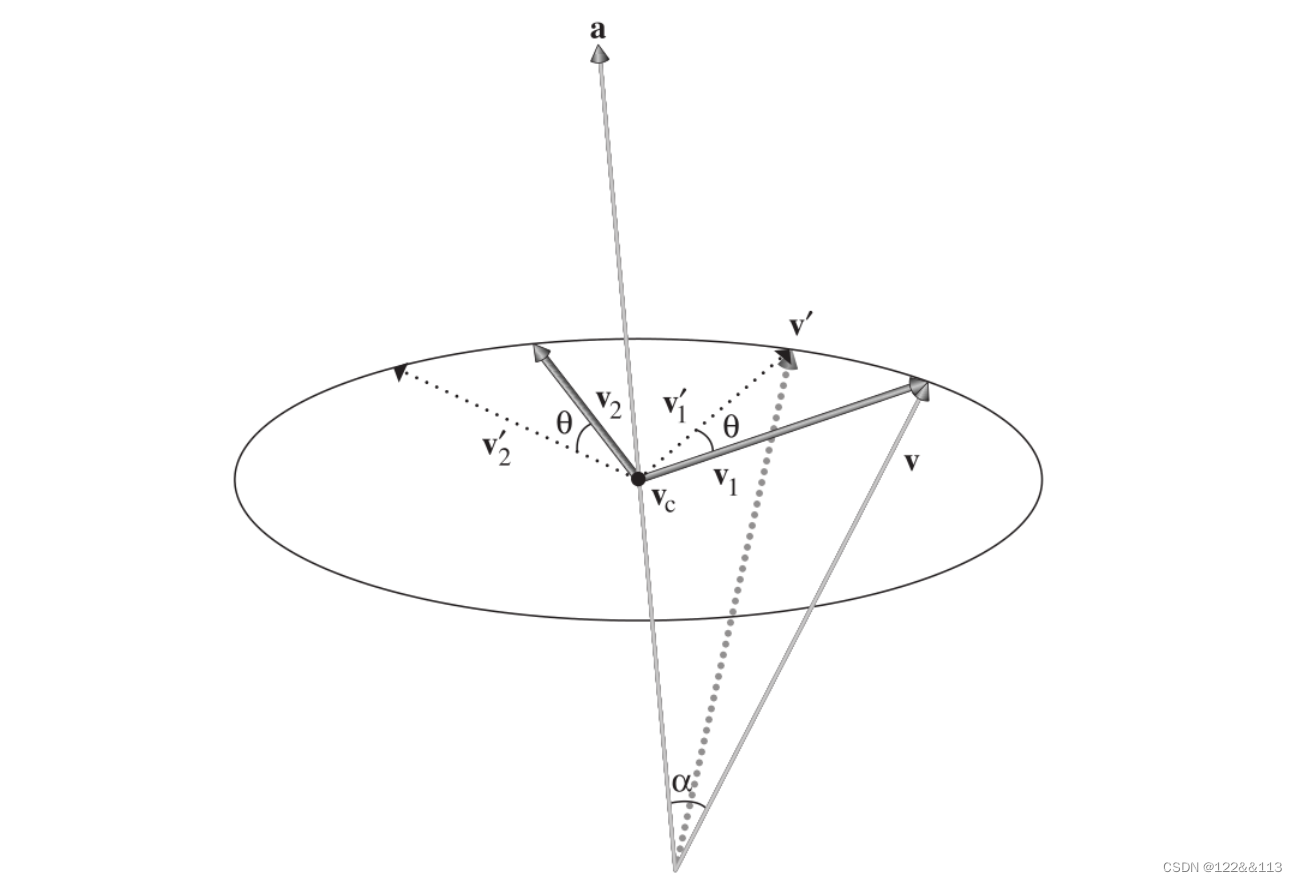



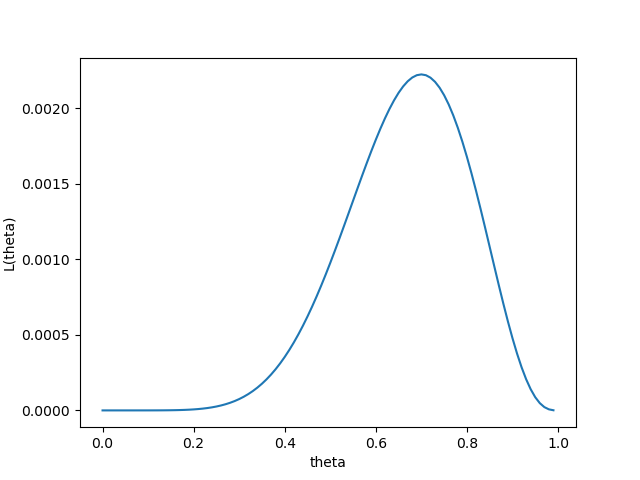





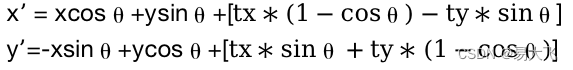
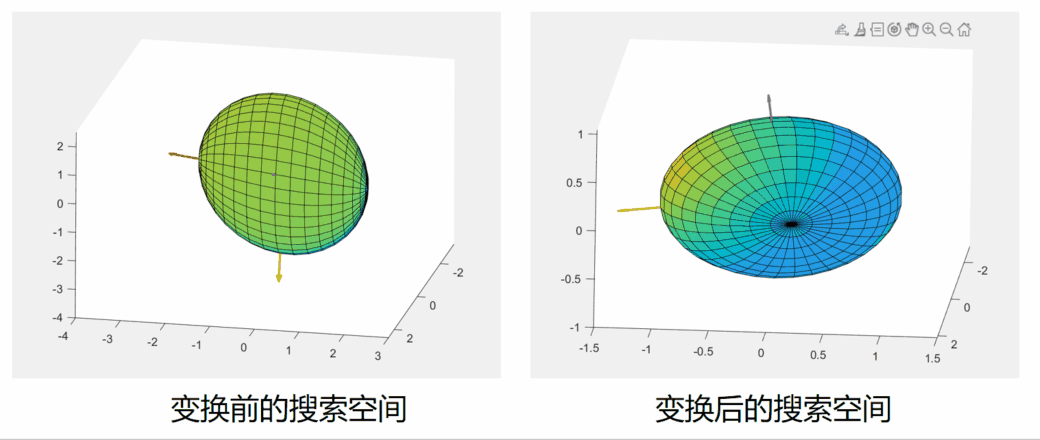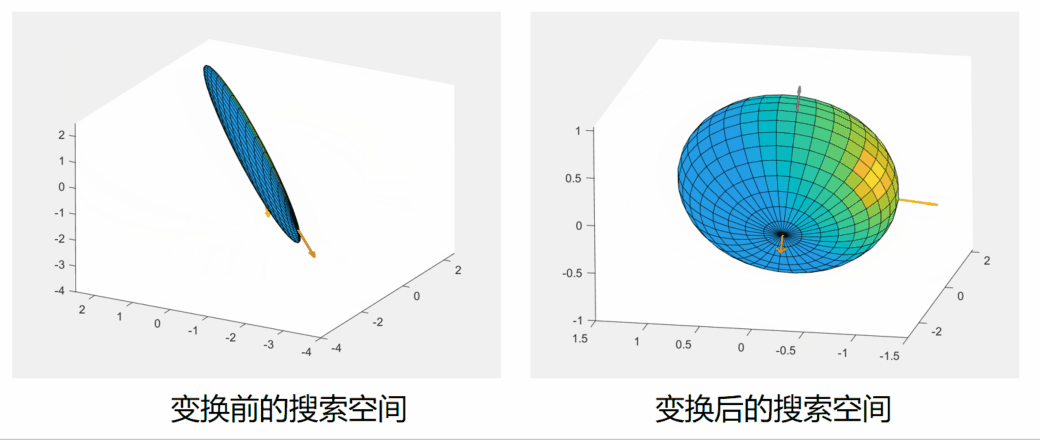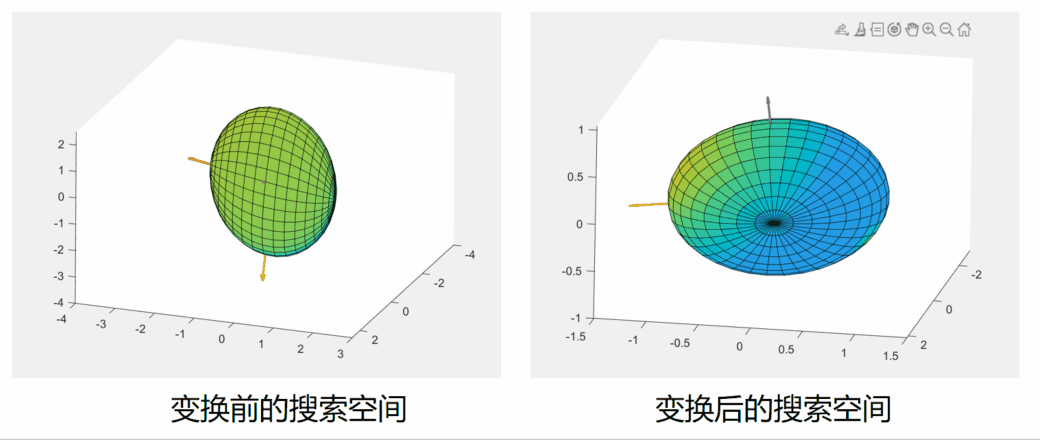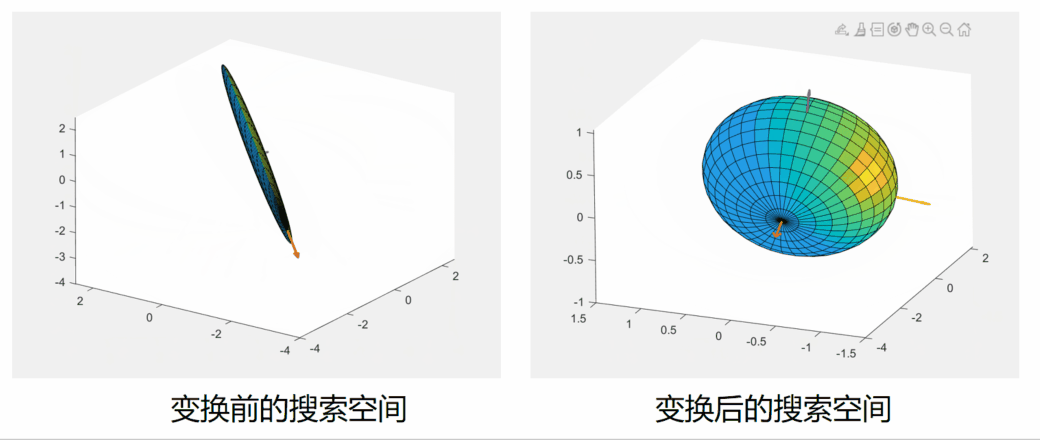


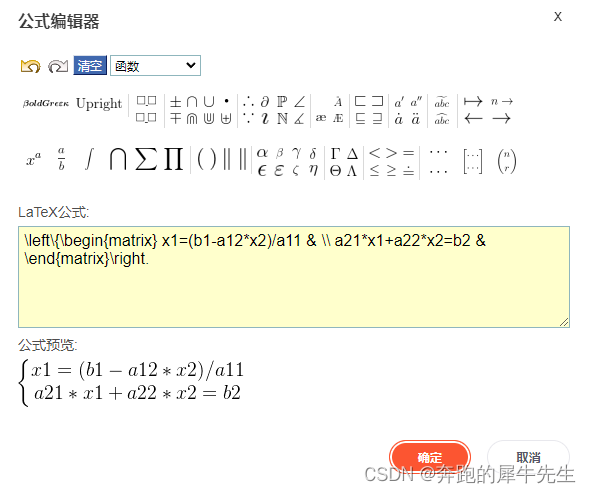
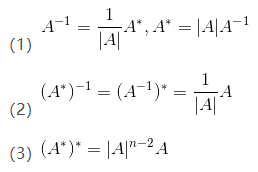
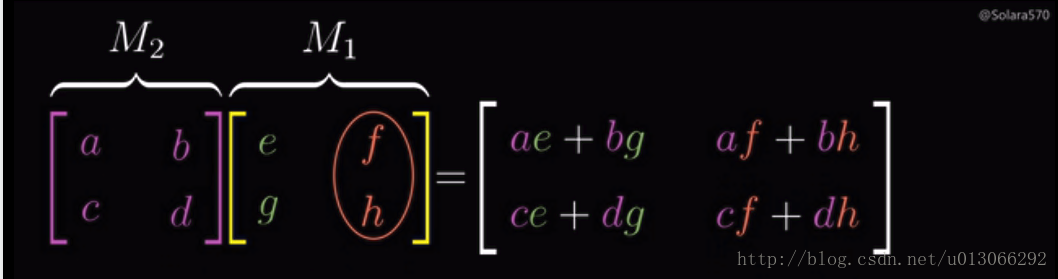
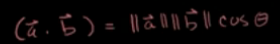




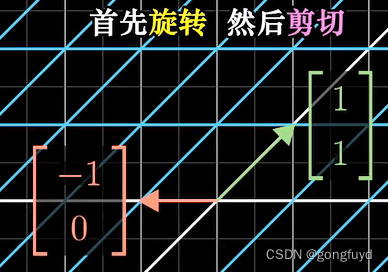
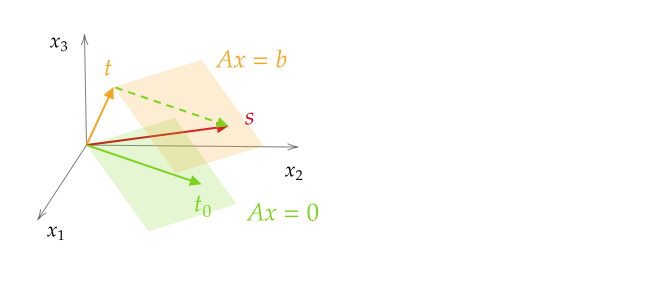

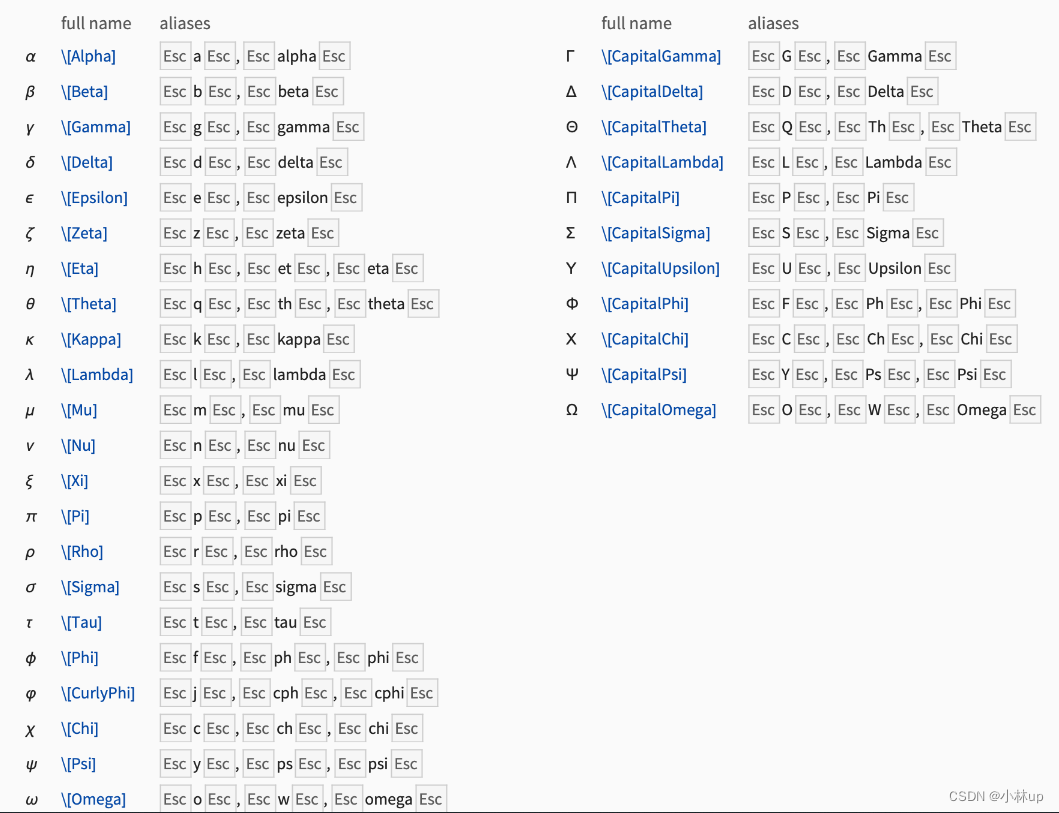
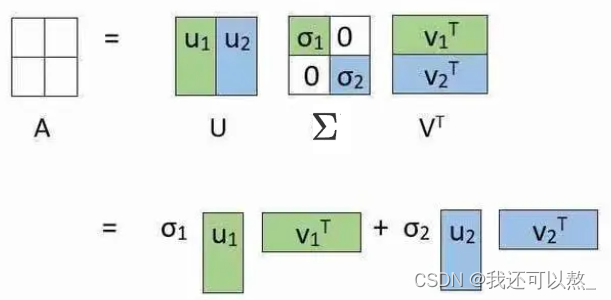


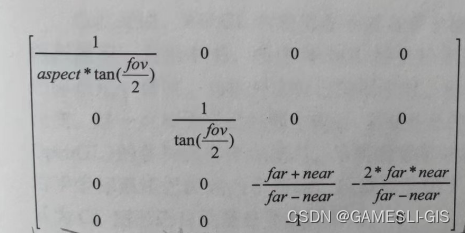



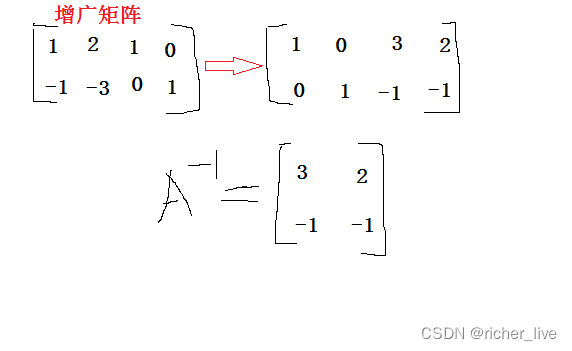


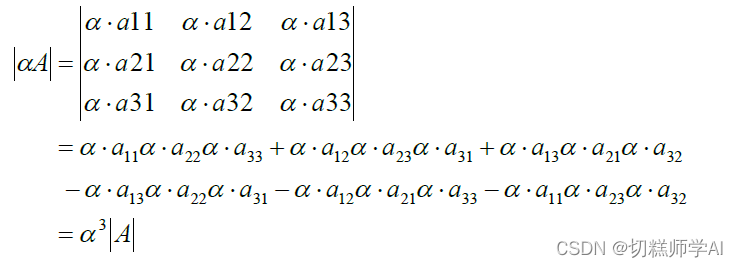


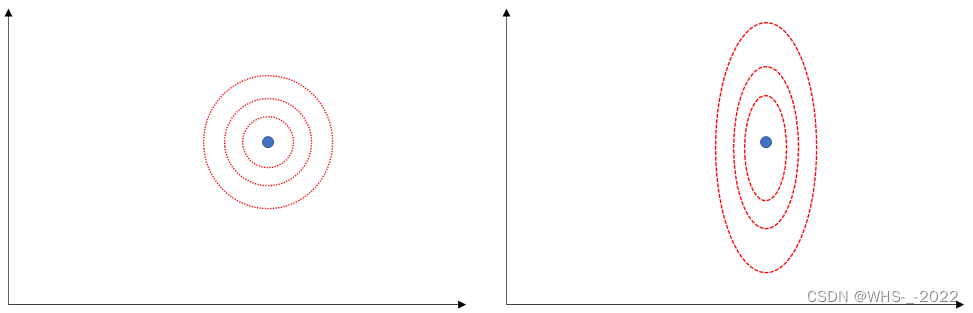




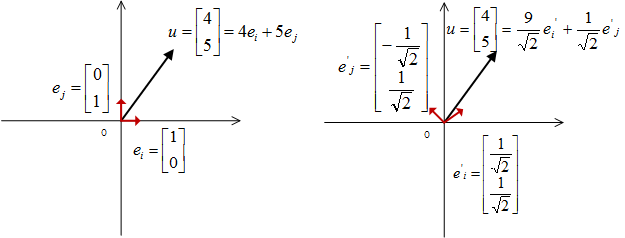
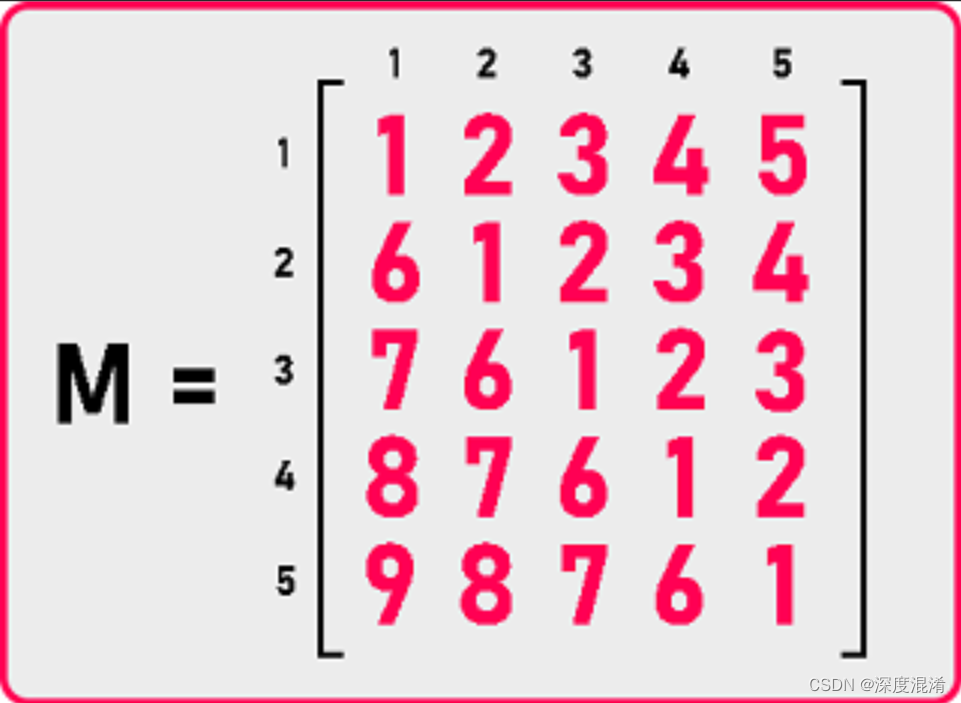
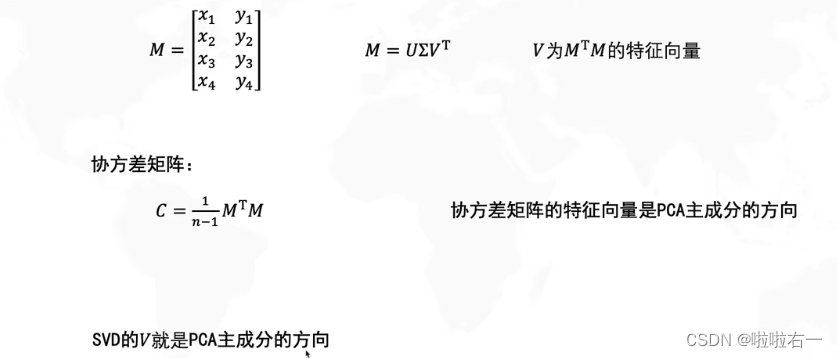
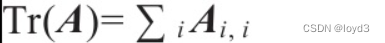

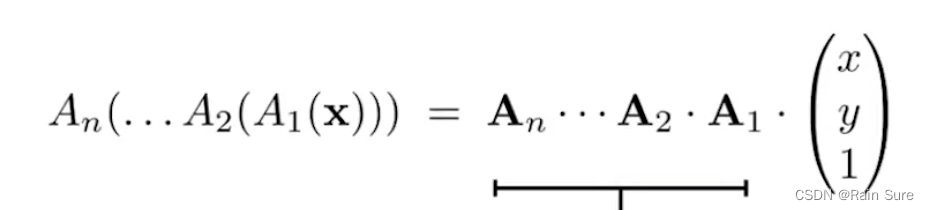

![[数学建模]主成分分析法PCA](https://img-blog.csdnimg.cn/d97e7fc16e6445caa1d0eee38be455ab.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5Luj56CB5pCs6L-Q5bel5bCP6I-c54uX,size_12,color_FFFFFF,t_70,g_se,x_16)

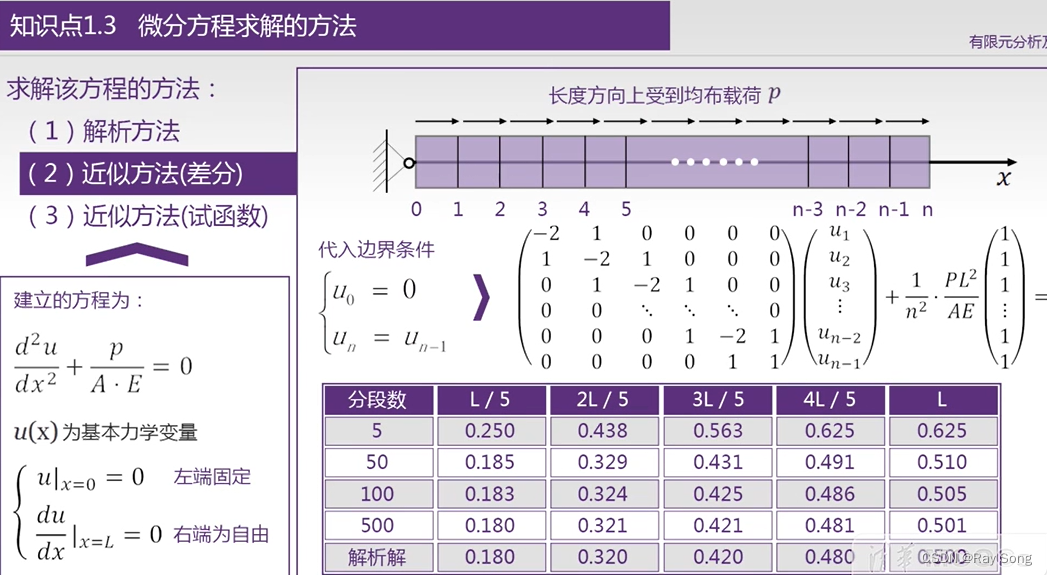
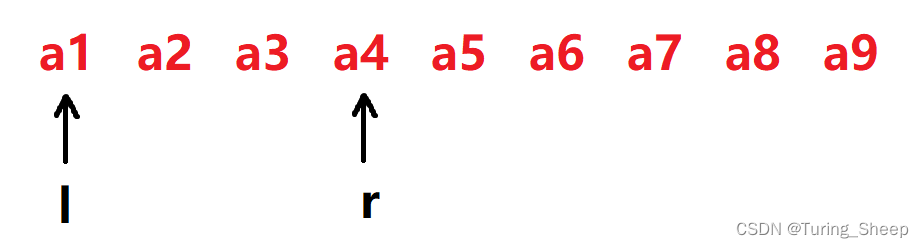











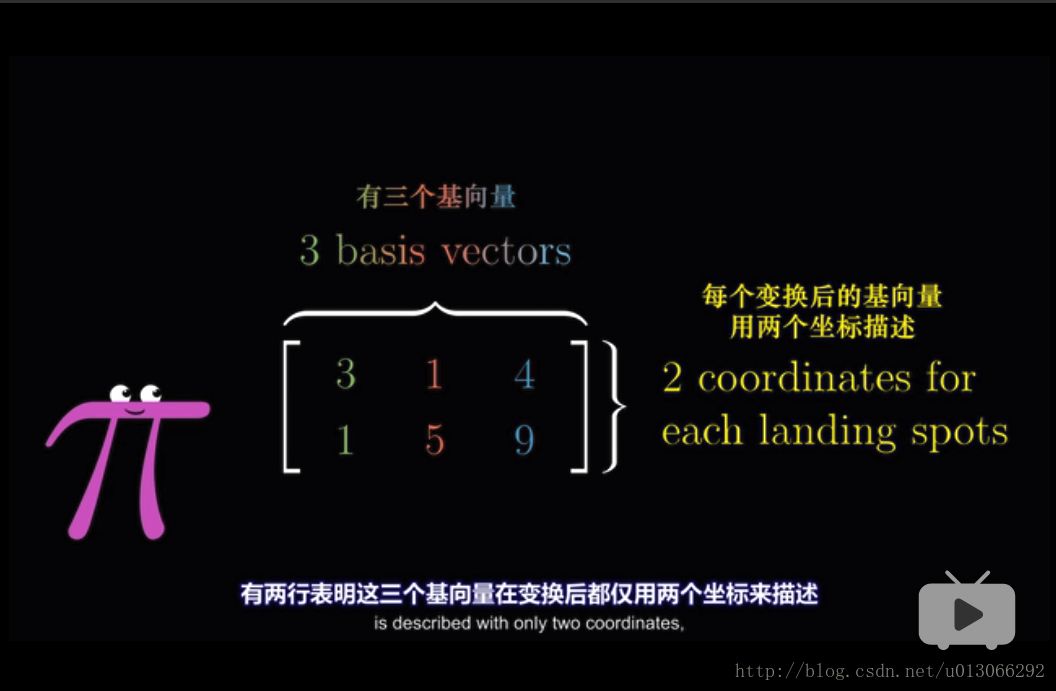


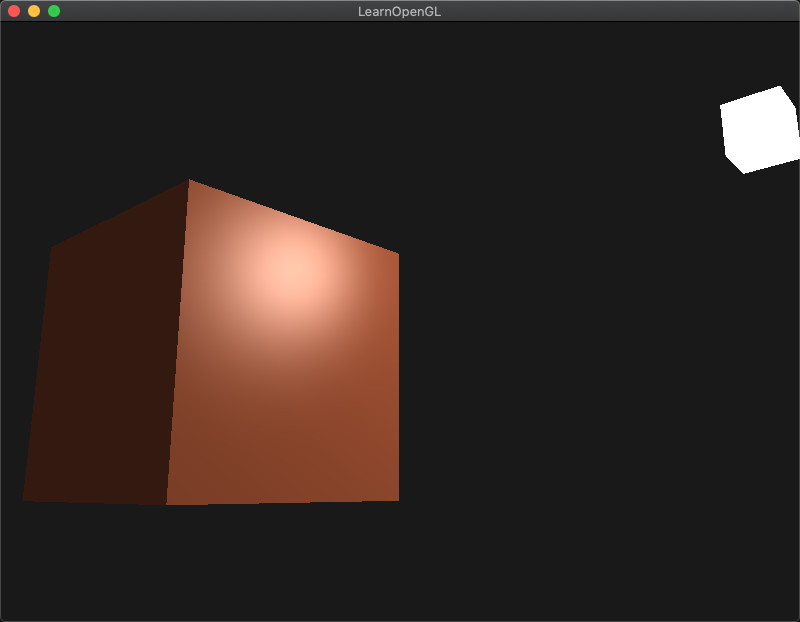

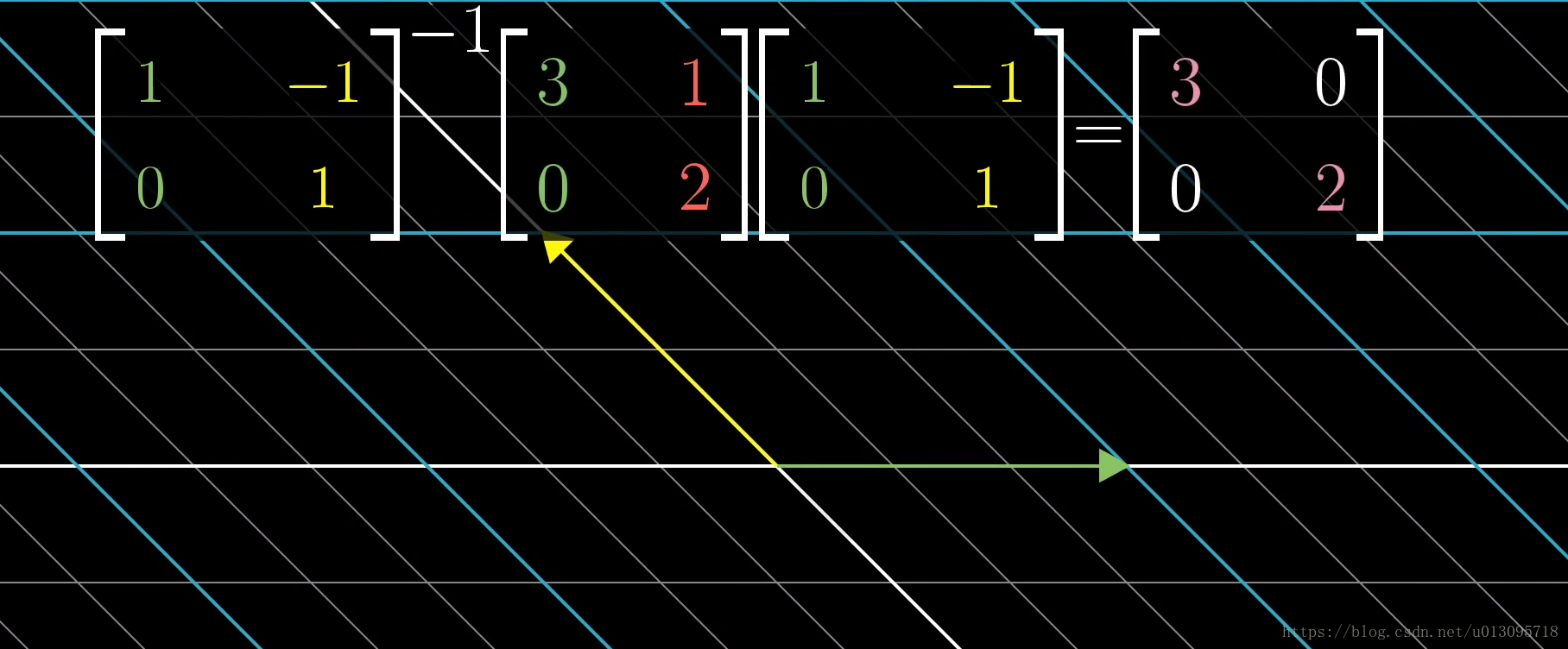
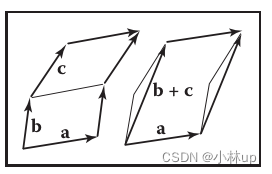
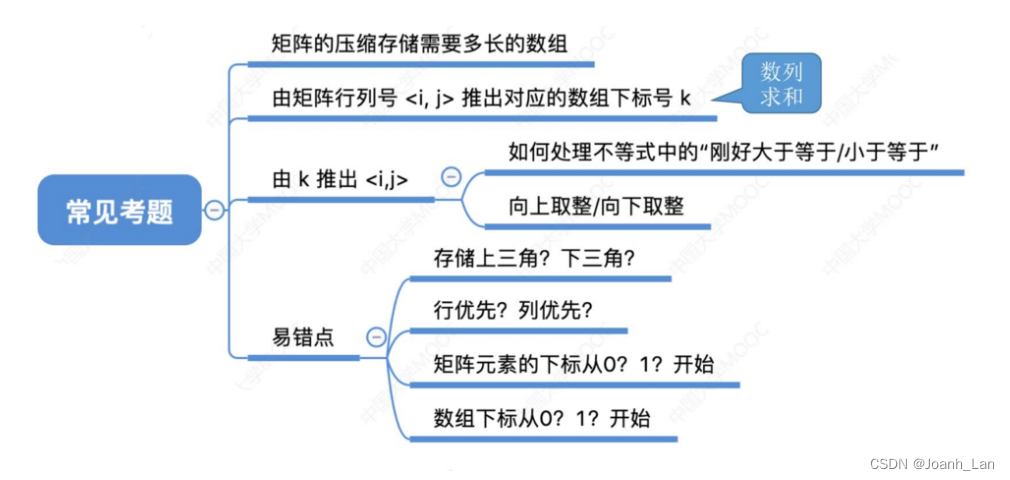






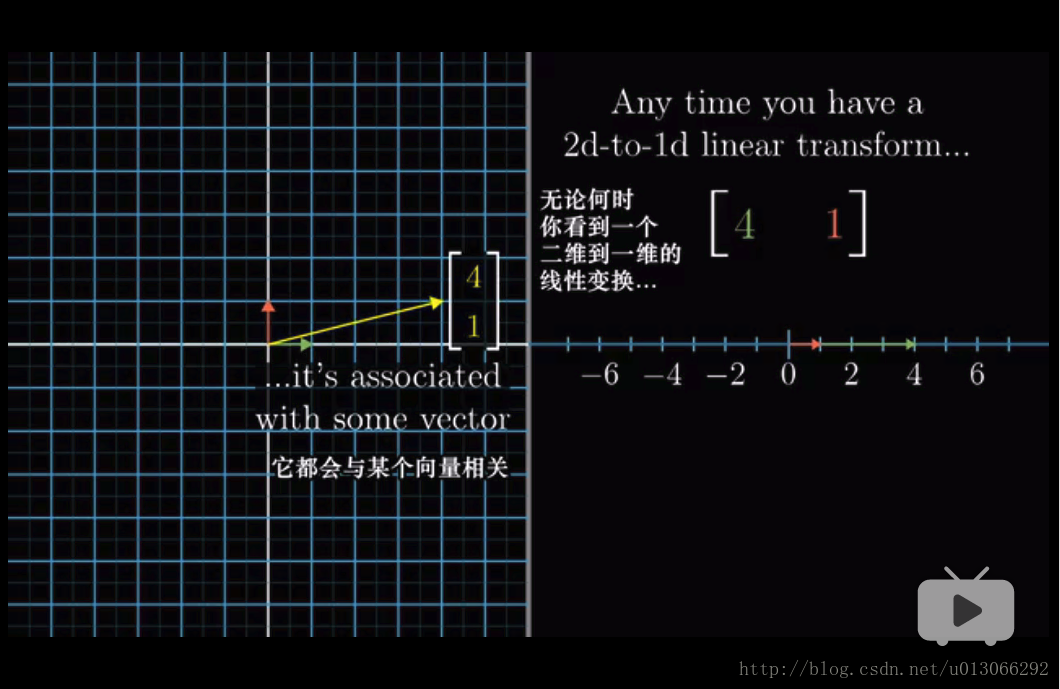







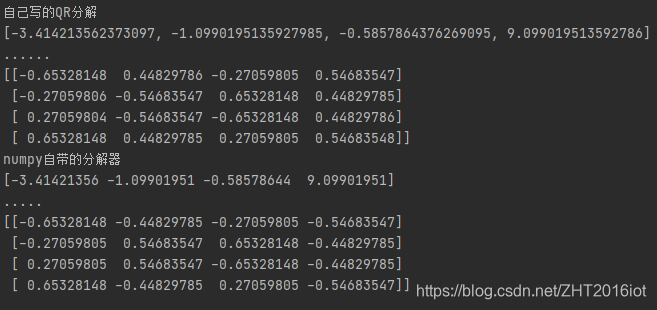
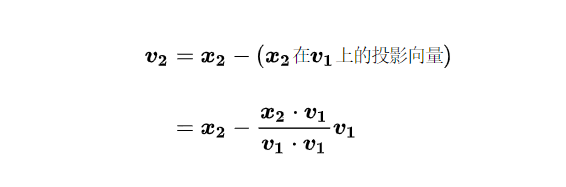

![matlab中各种括号(),[],与{}的区别与认识](https://img-blog.csdn.net/20161020160756688)



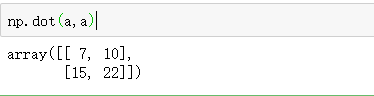


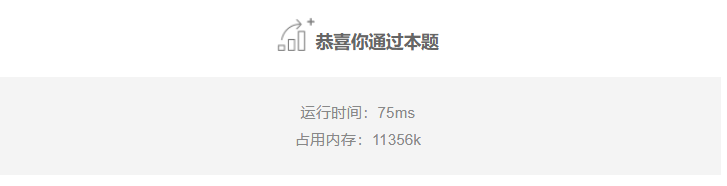









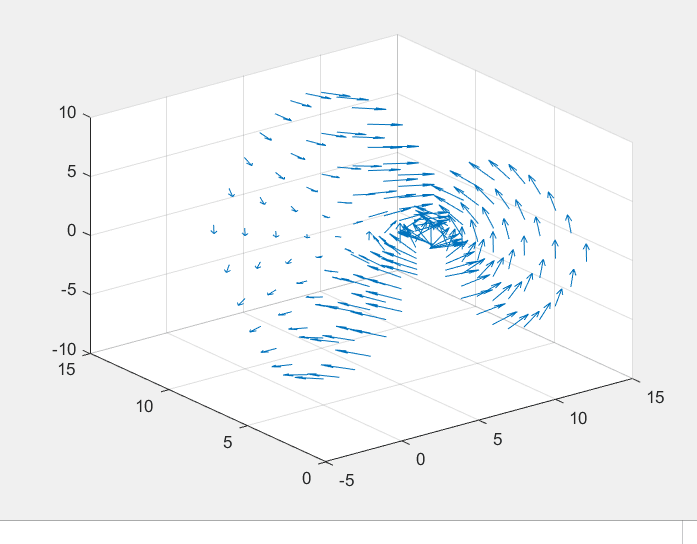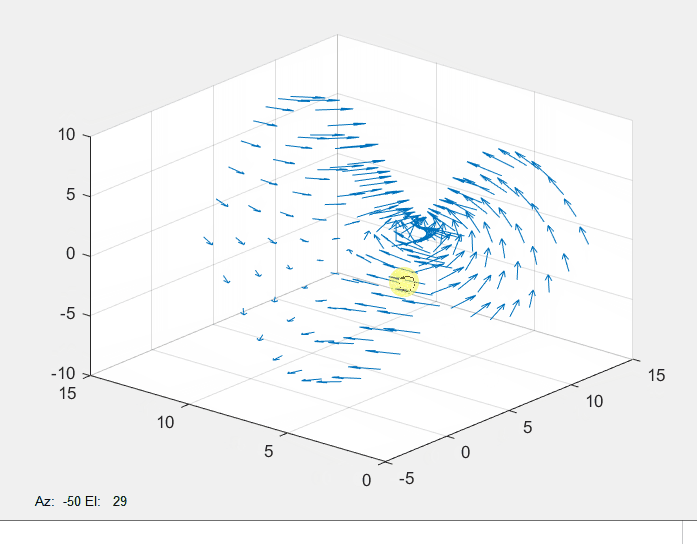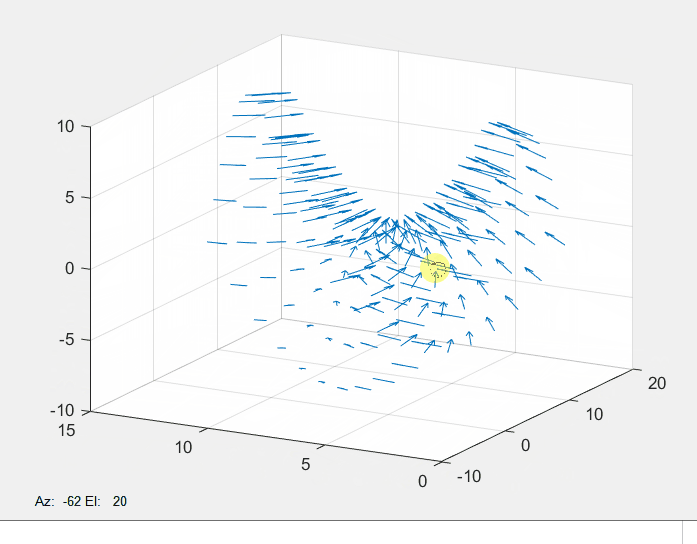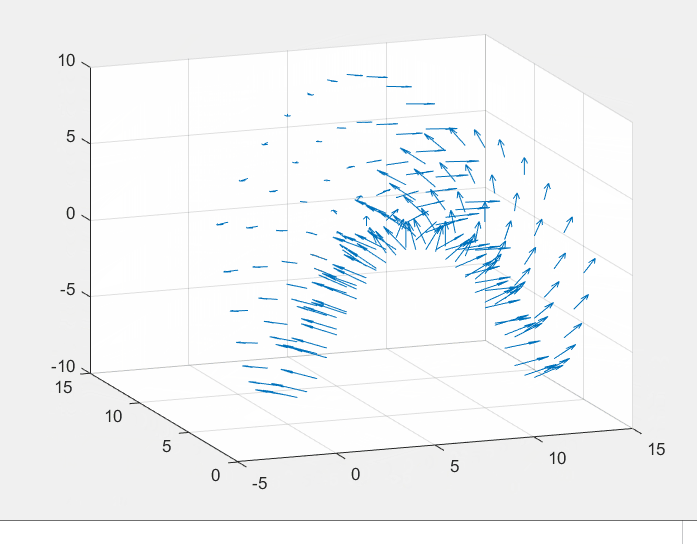
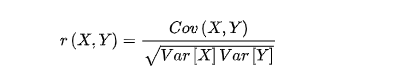







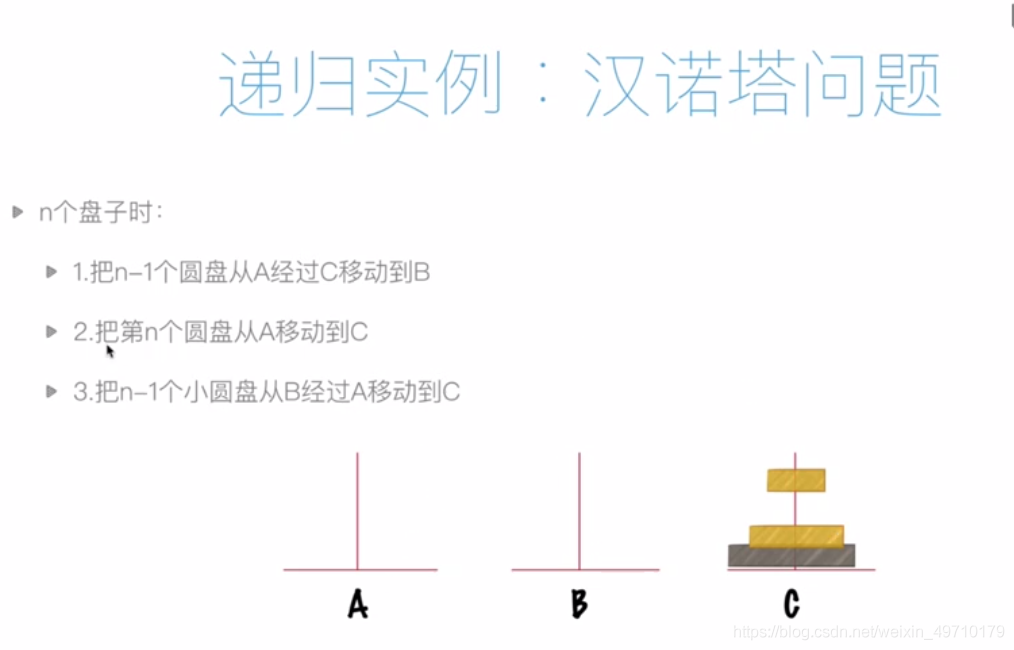











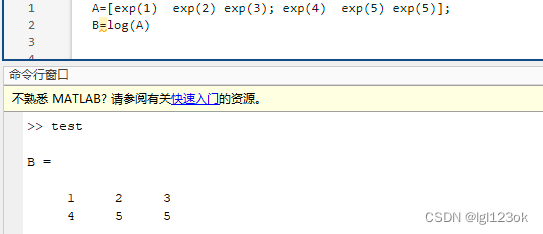

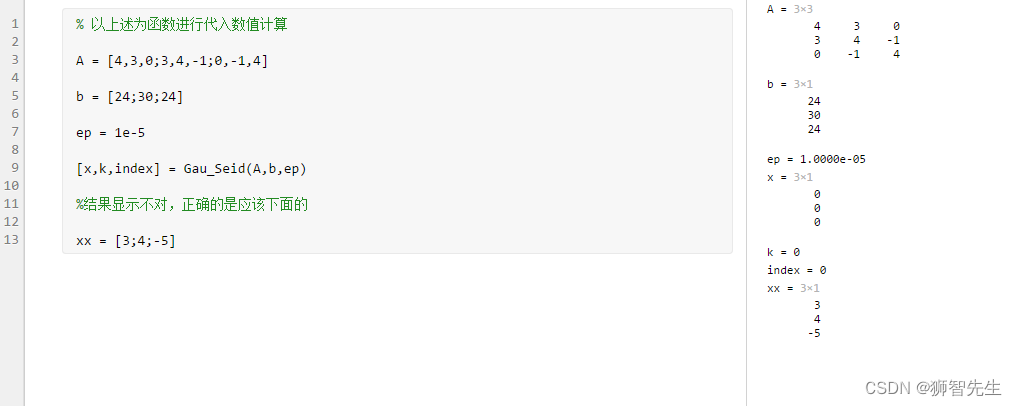

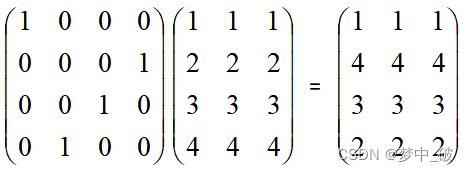












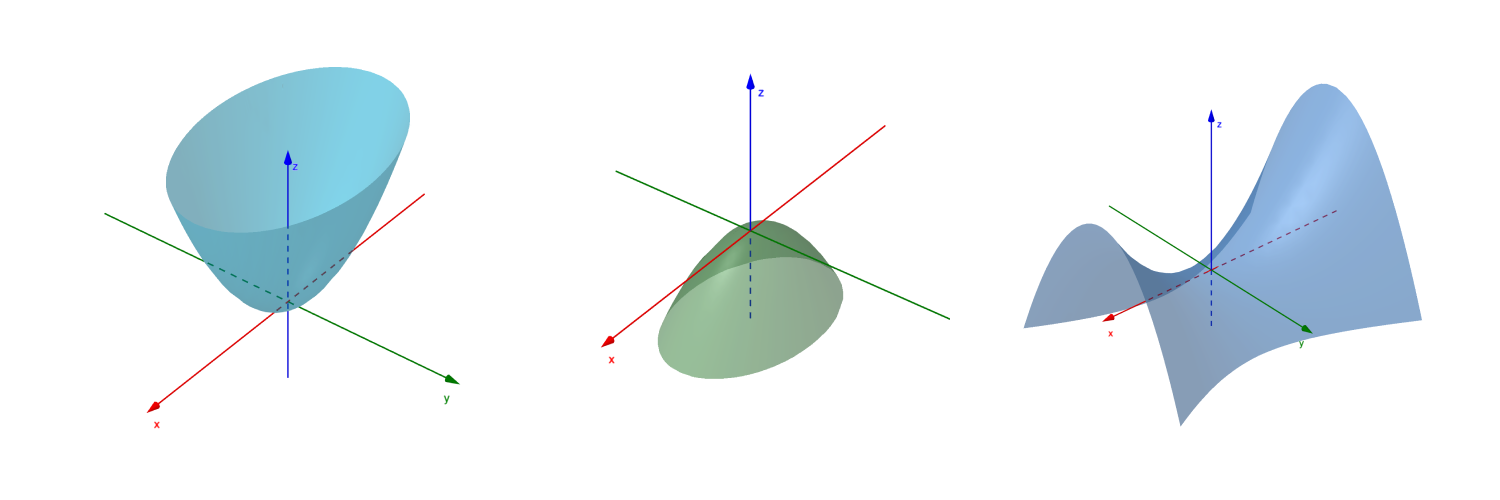



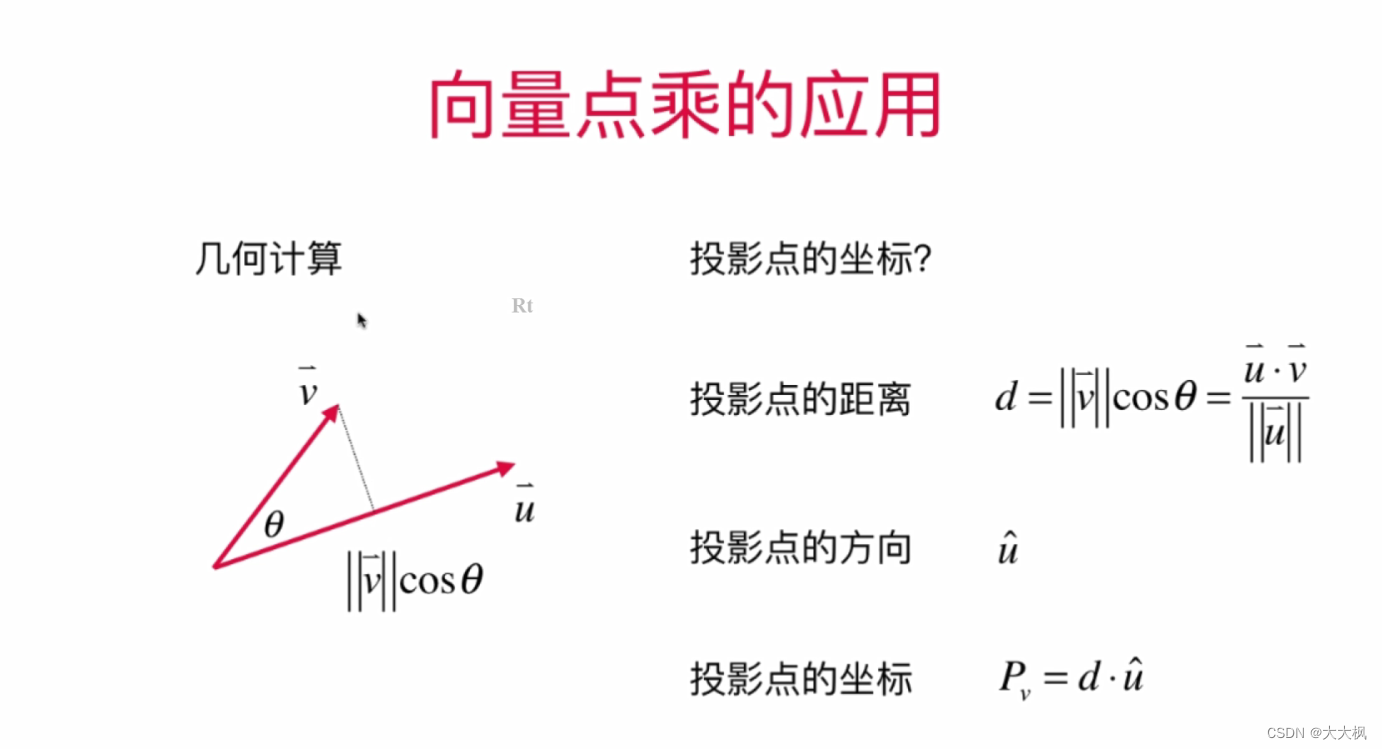
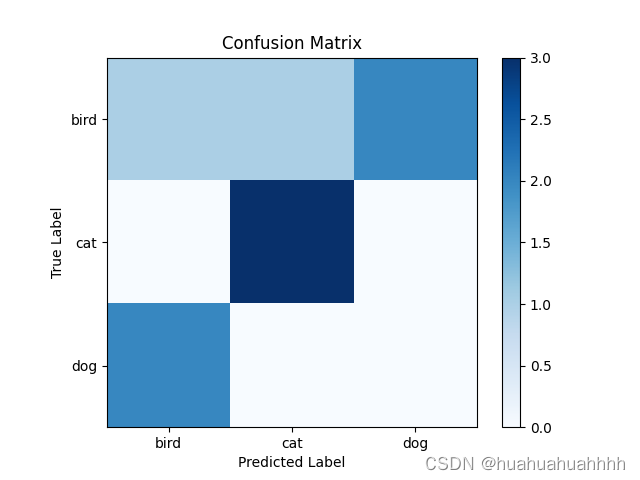

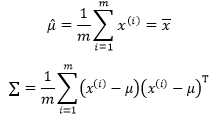

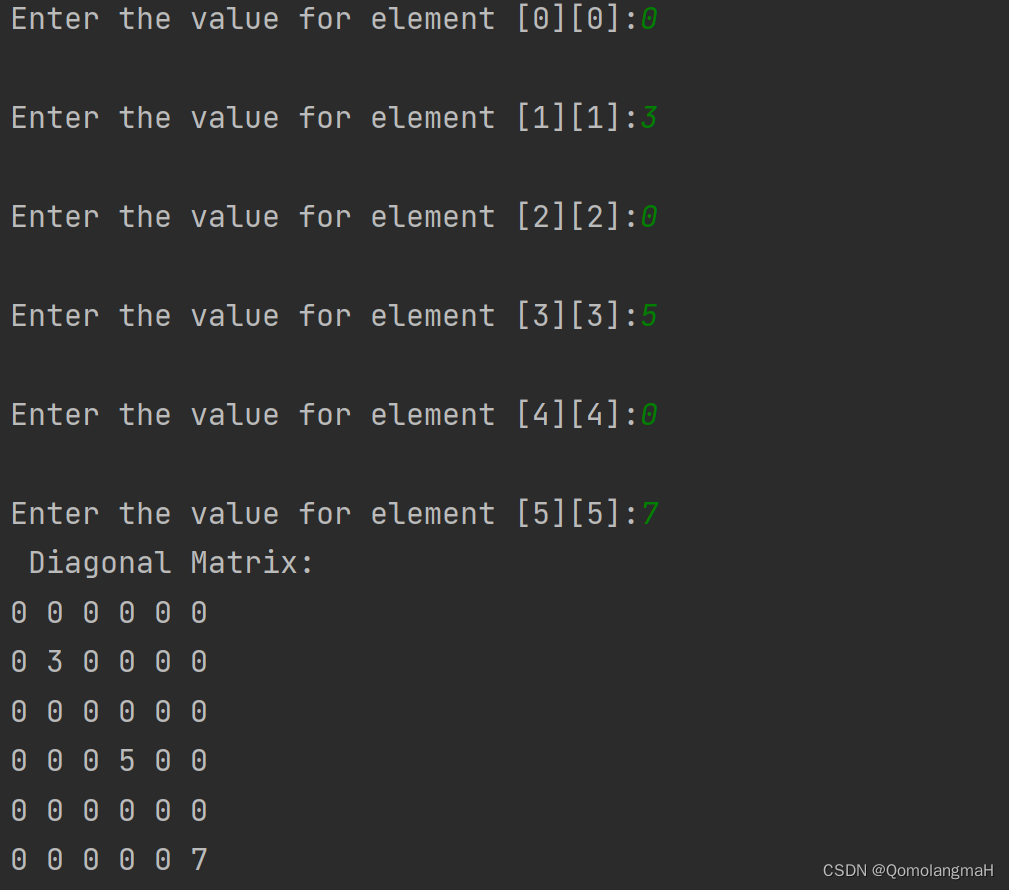







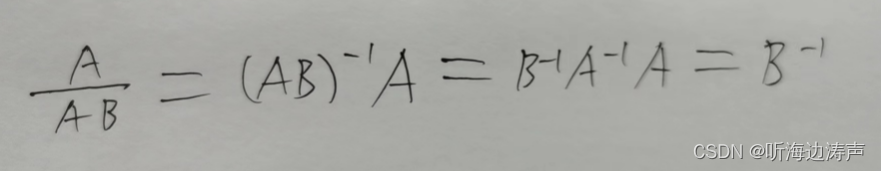

![[量子计算与量子信息] 2.1 线性代数](https://img-blog.csdnimg.cn/img_convert/29c4f41b3e830e7484fef6be74d04ae0.png)
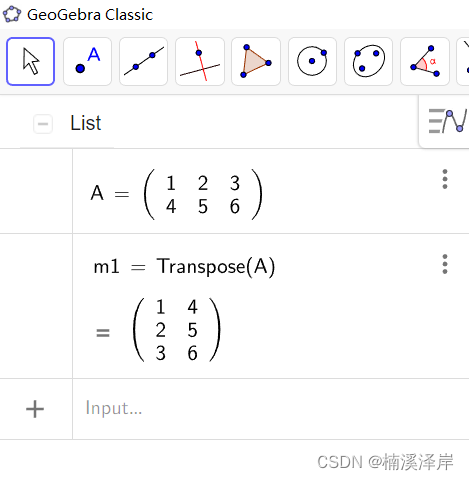




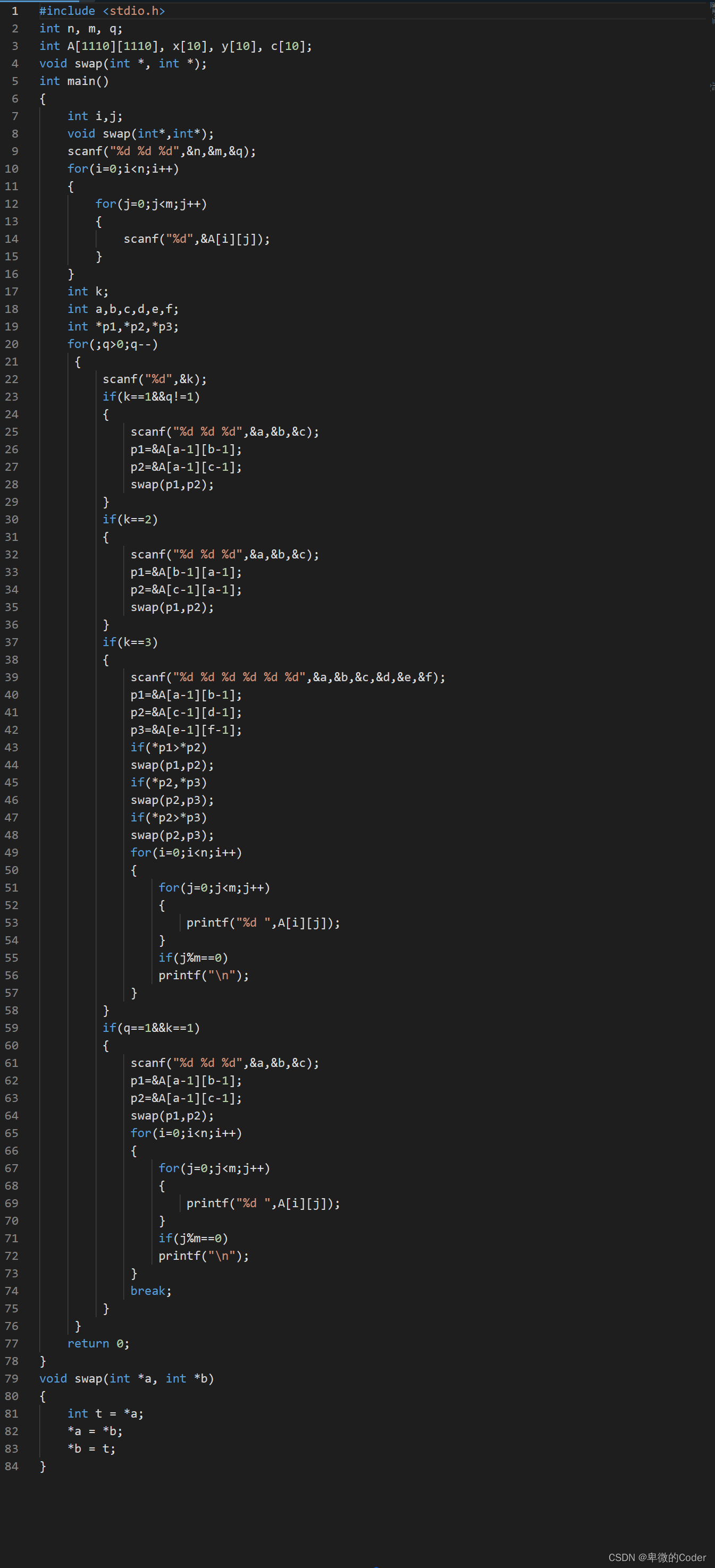


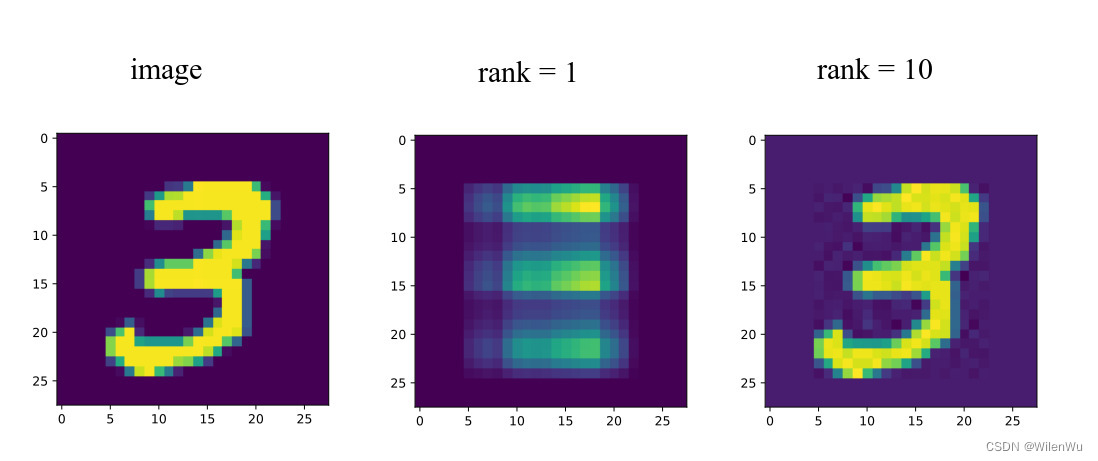
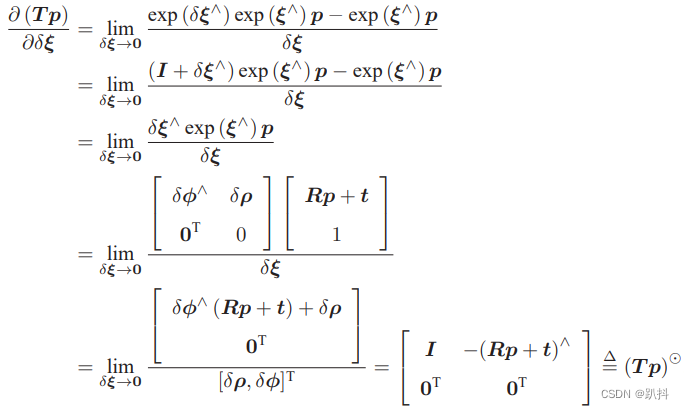




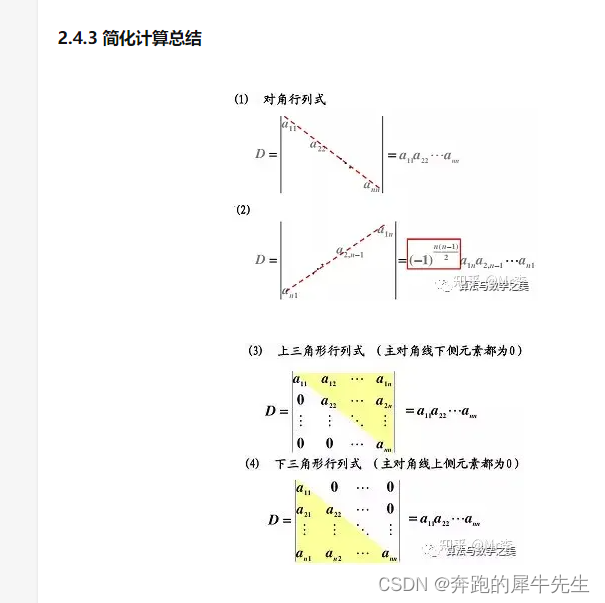



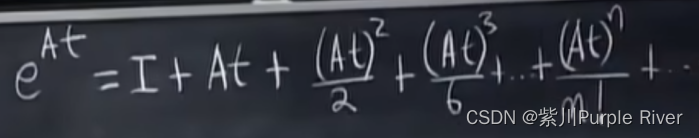



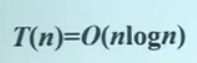




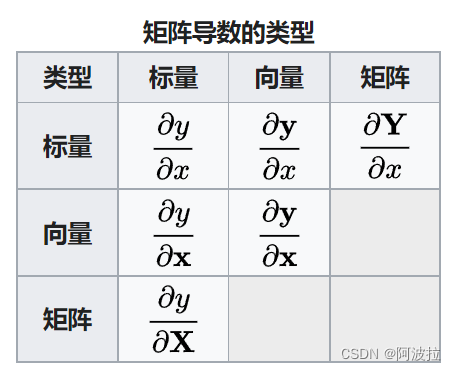


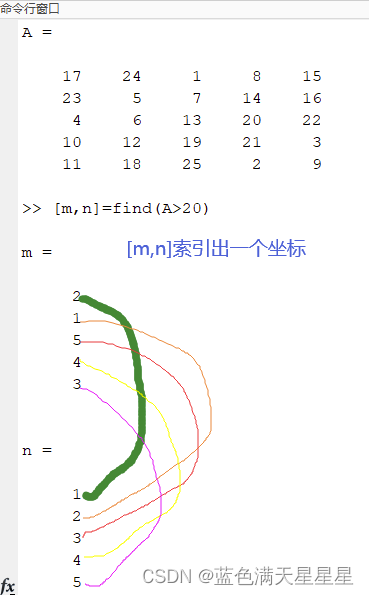


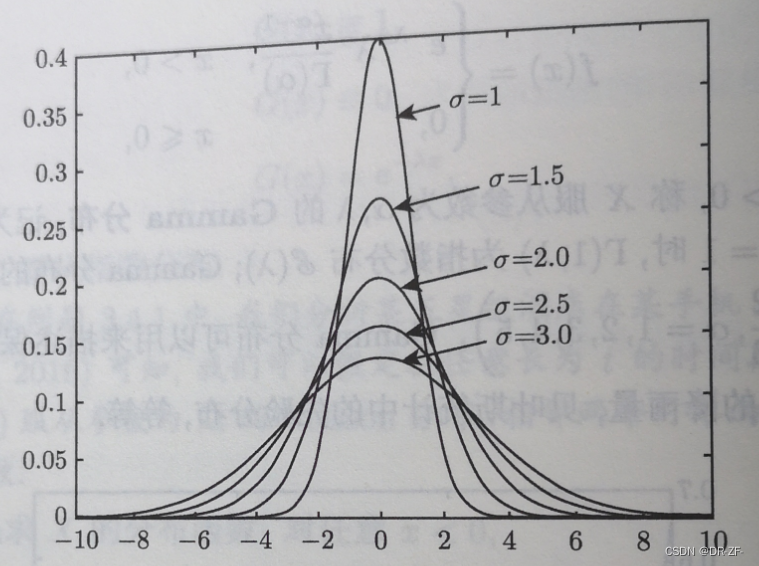




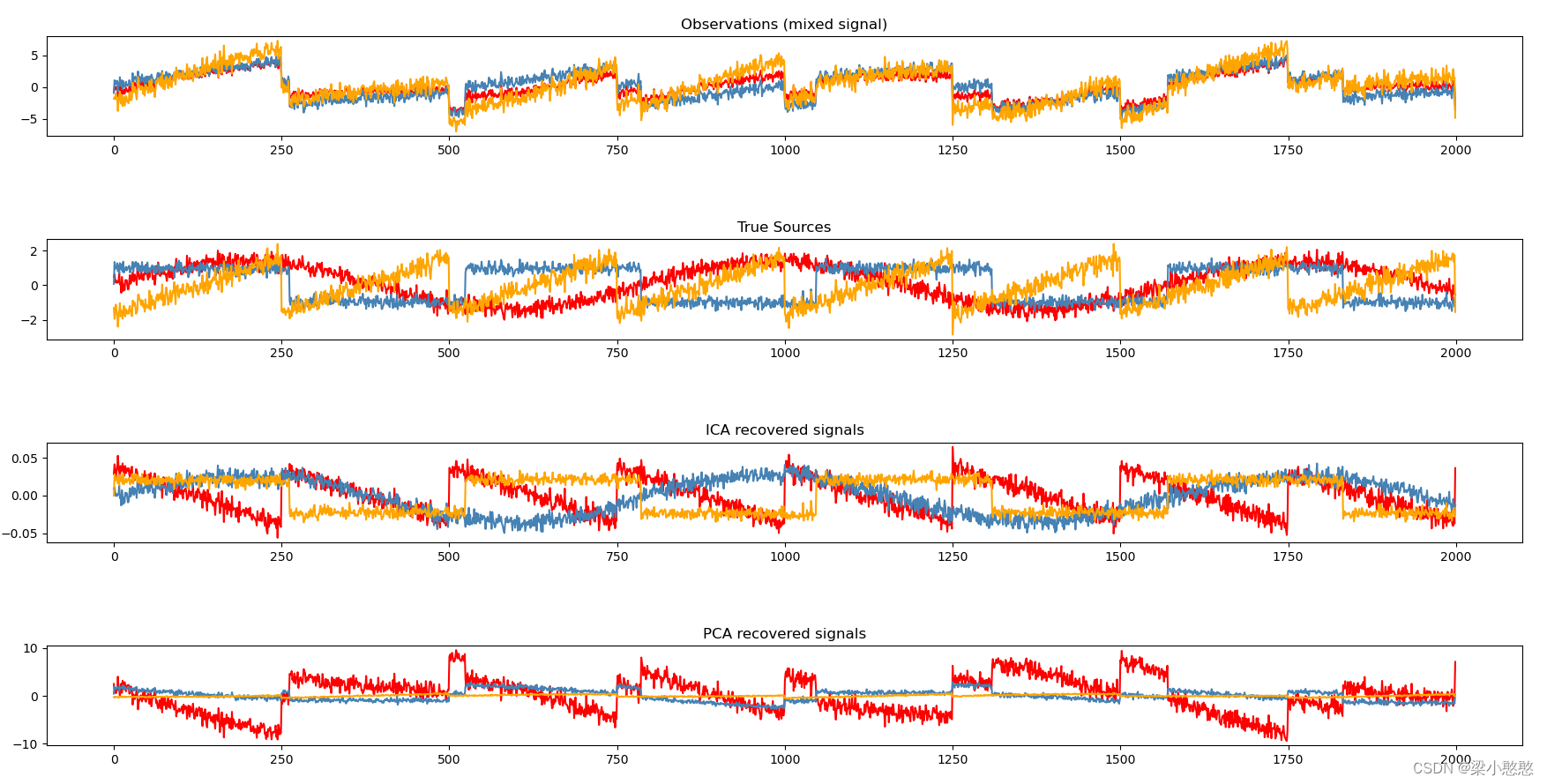

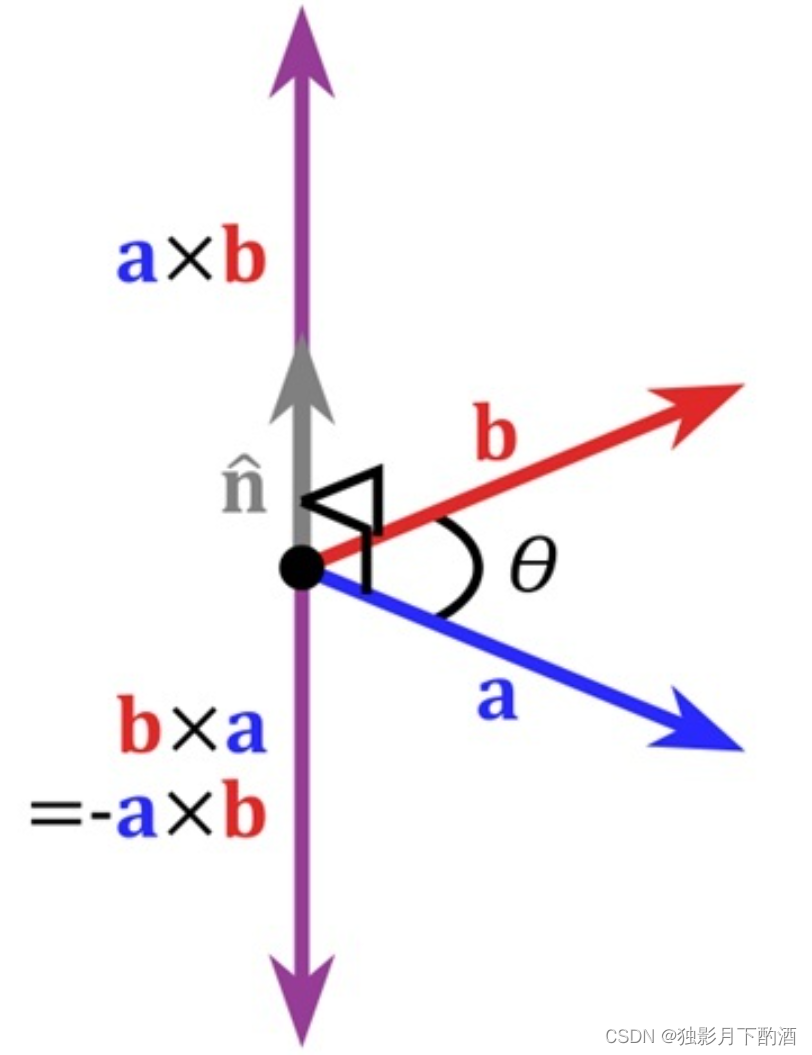






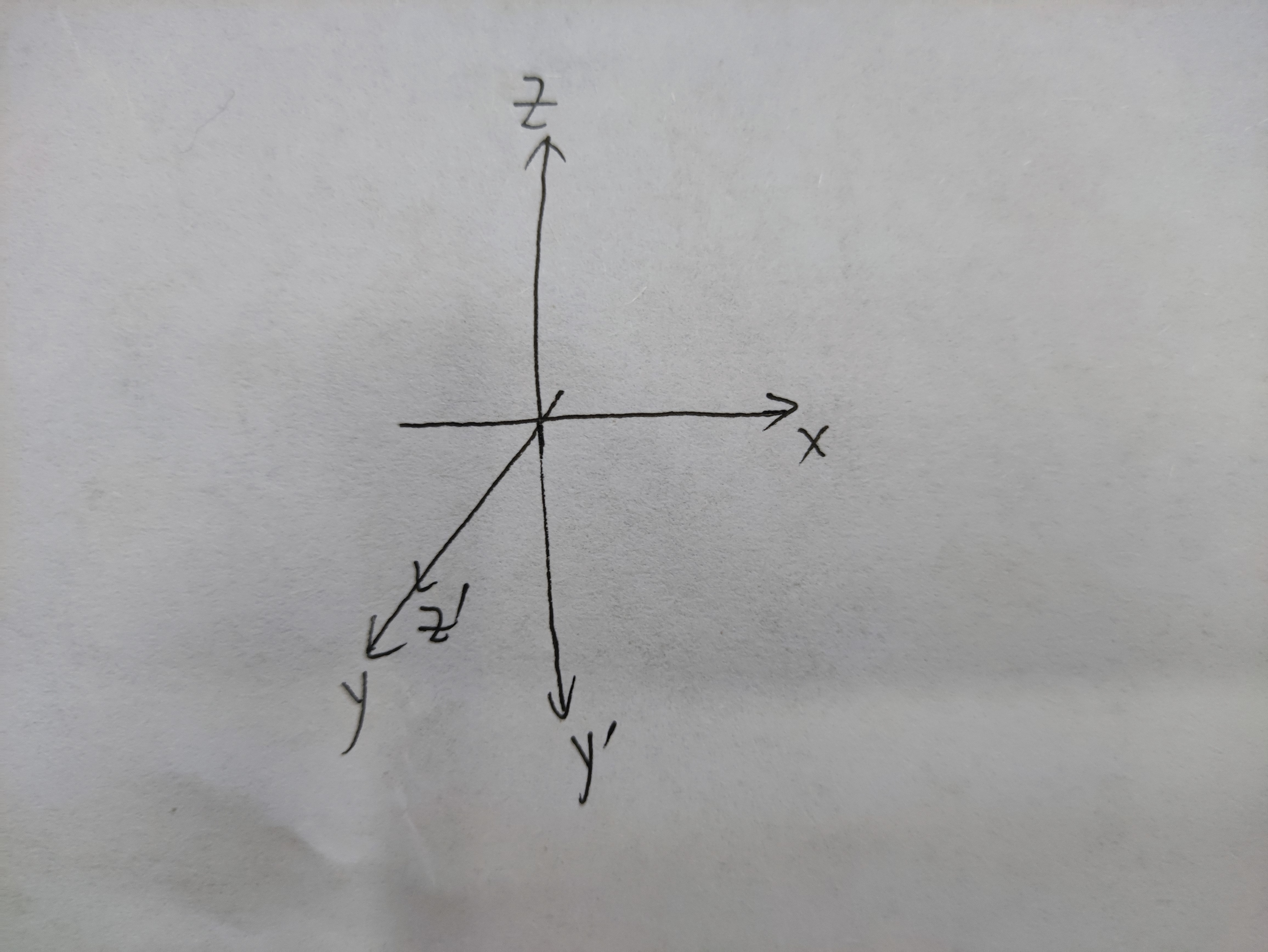



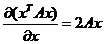



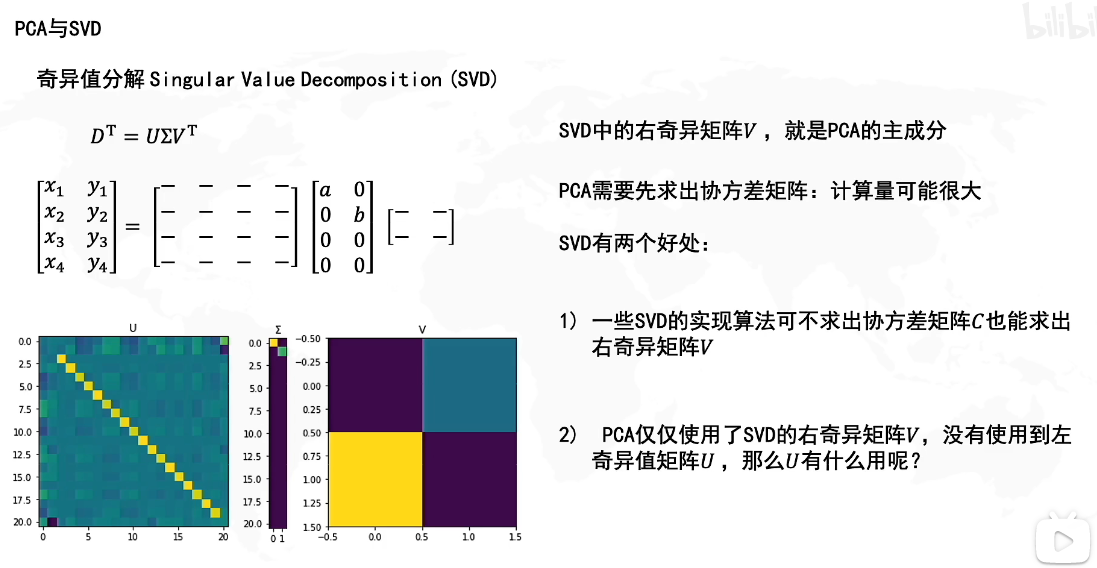



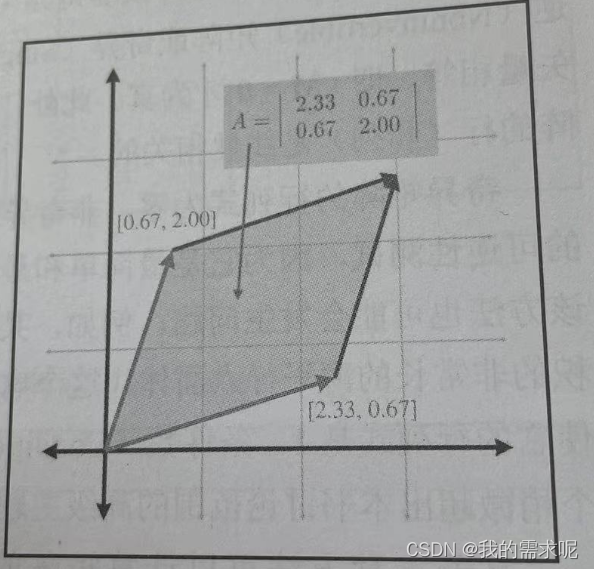





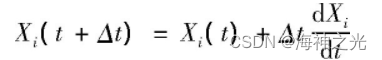
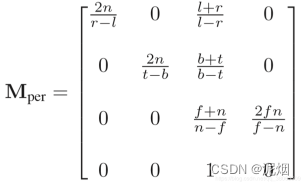

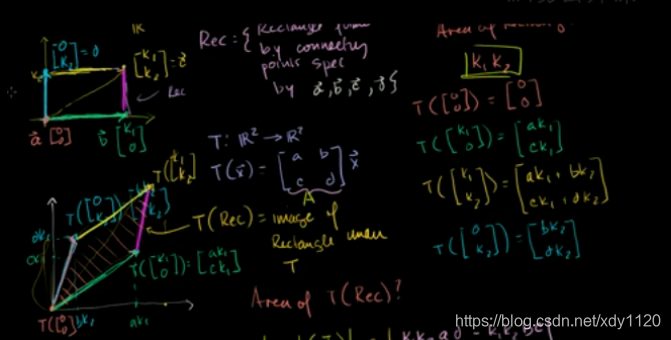







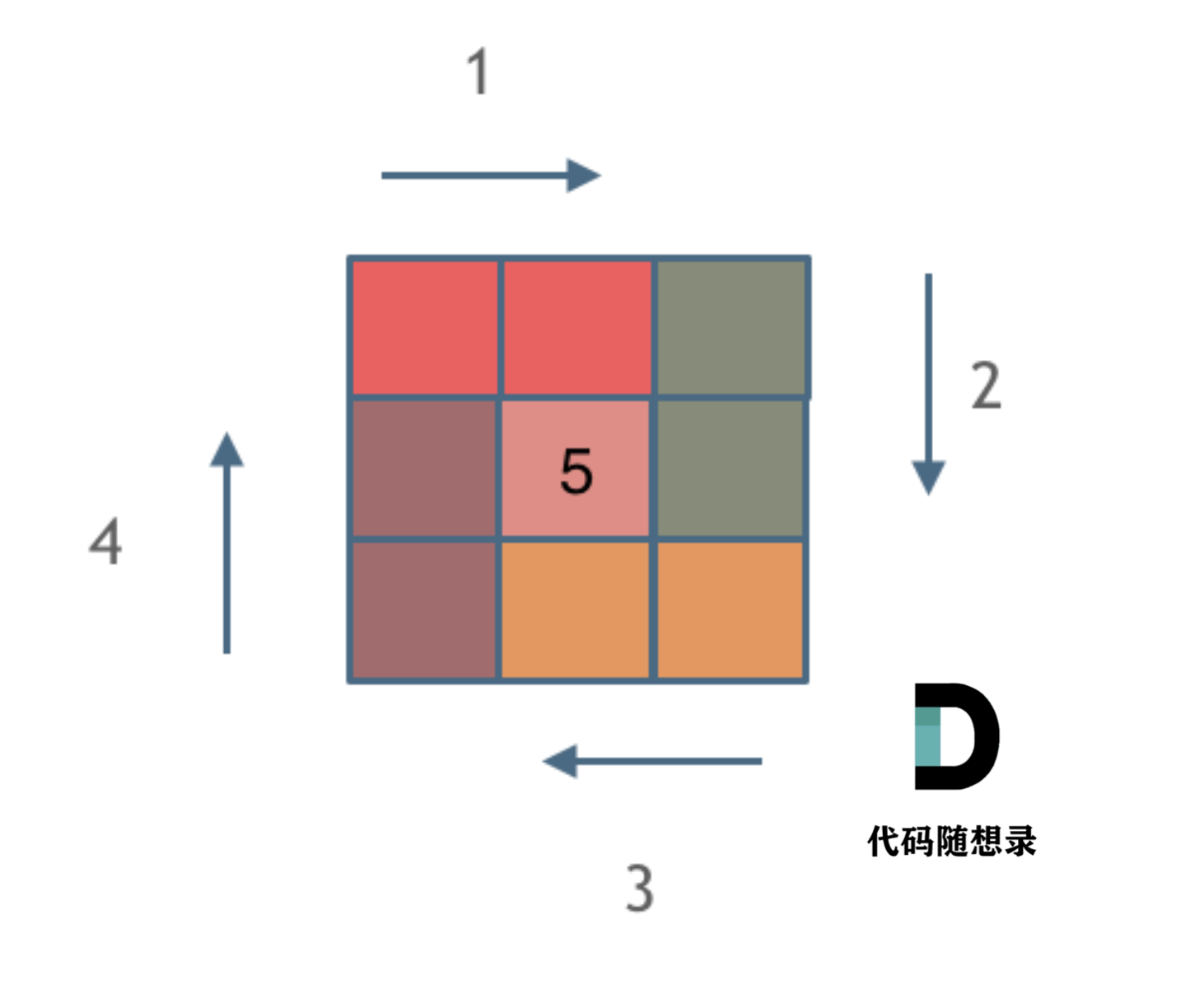



![[解题报告]【第35题】给定两个 a X b 和 c X d 的矩阵 ,求两个矩阵的乘积](https://img-blog.csdnimg.cn/b31eeae94c9441cf8141453018835763.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAWGluZ2xlaUdhbw==,size_20,color_FFFFFF,t_70,g_se,x_16)

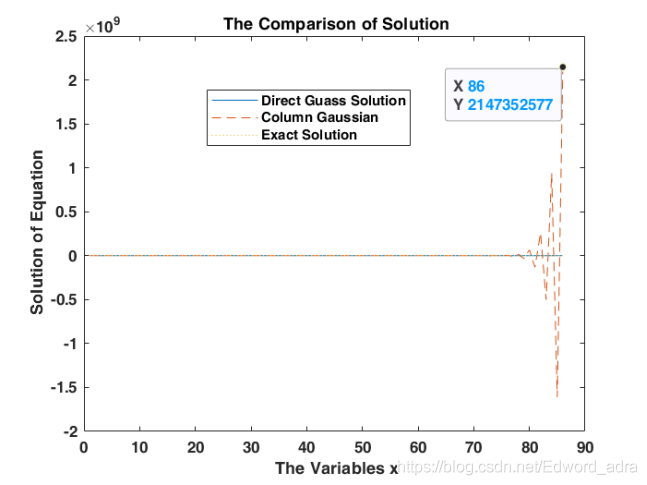

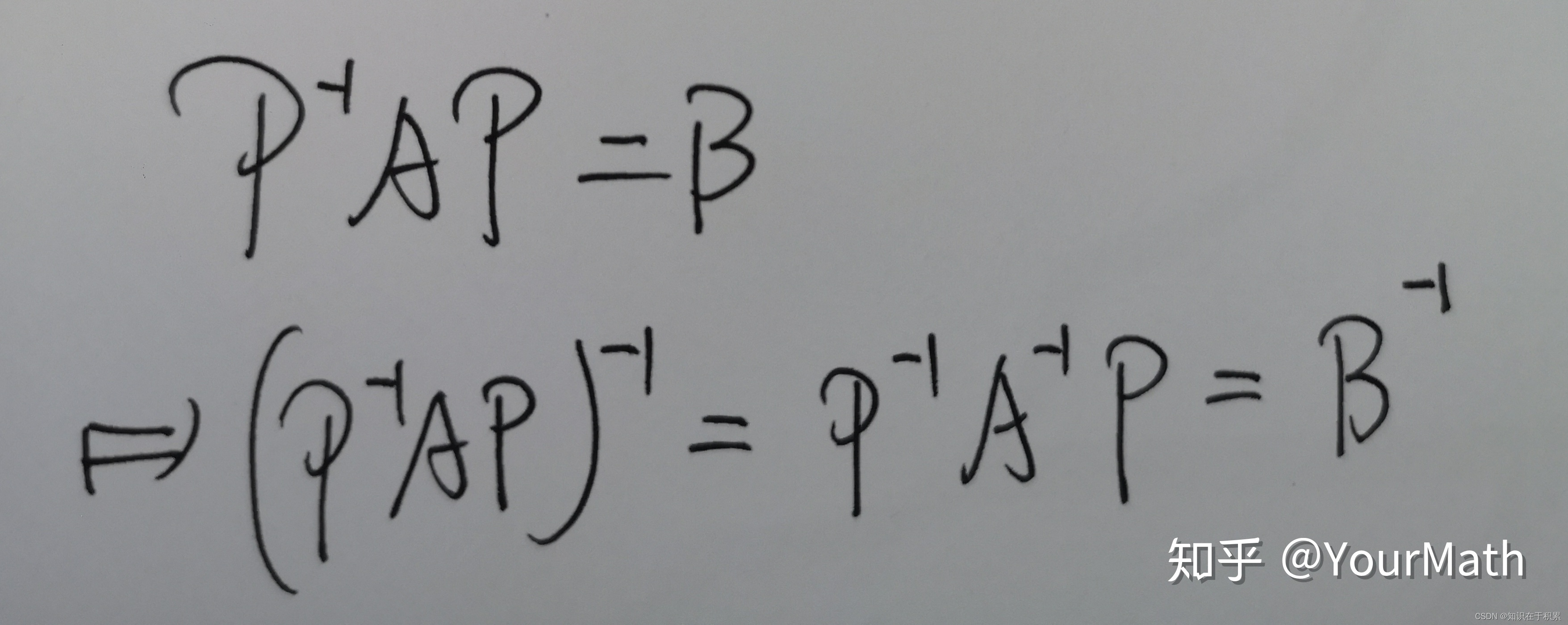
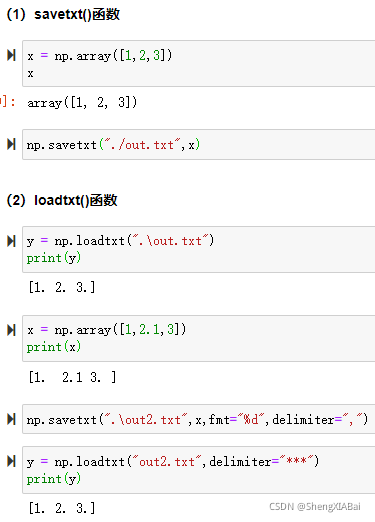




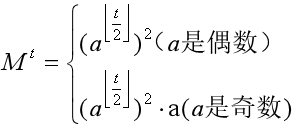
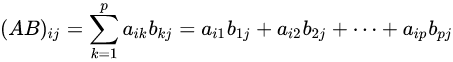


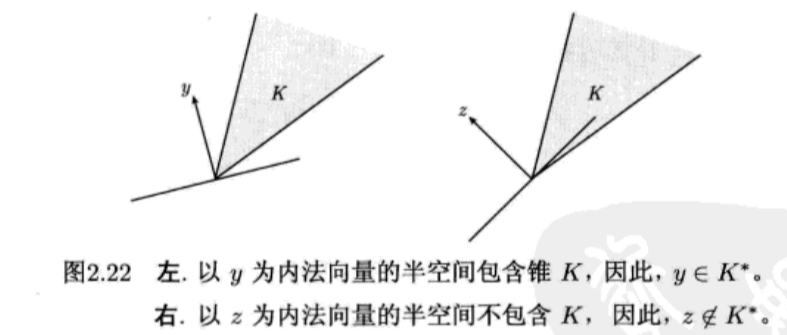













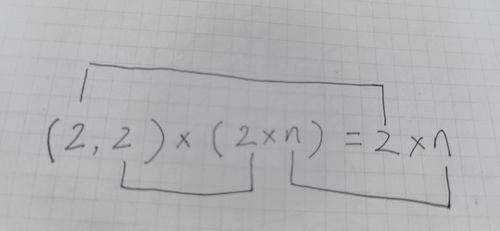
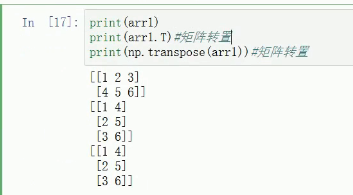
![P4035 [JSOI2008]球形空间产生器 ——高斯消元](https://img-blog.csdnimg.cn/bd3466cb01b14ba6aabd9f51200c91b8.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAU3RyZXppYQ==,size_20,color_FFFFFF,t_70,g_se,x_16)

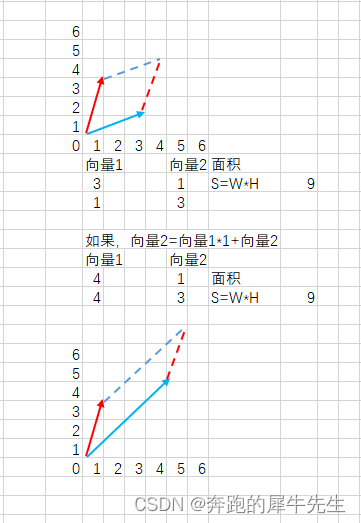

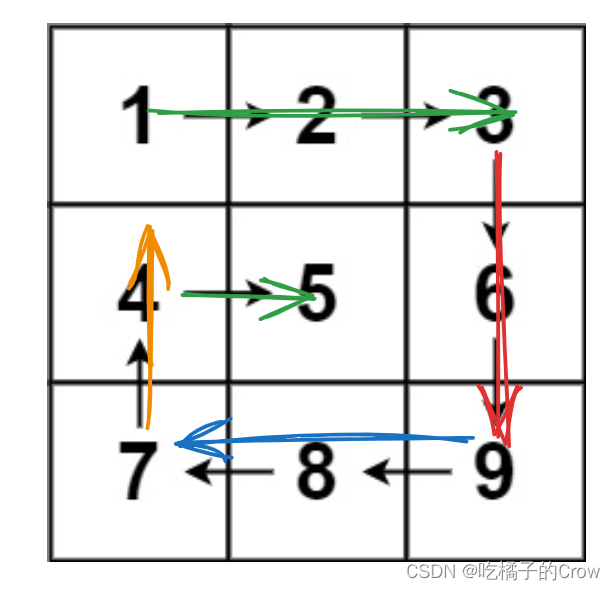
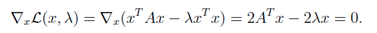






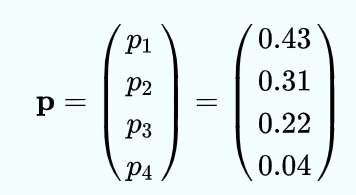
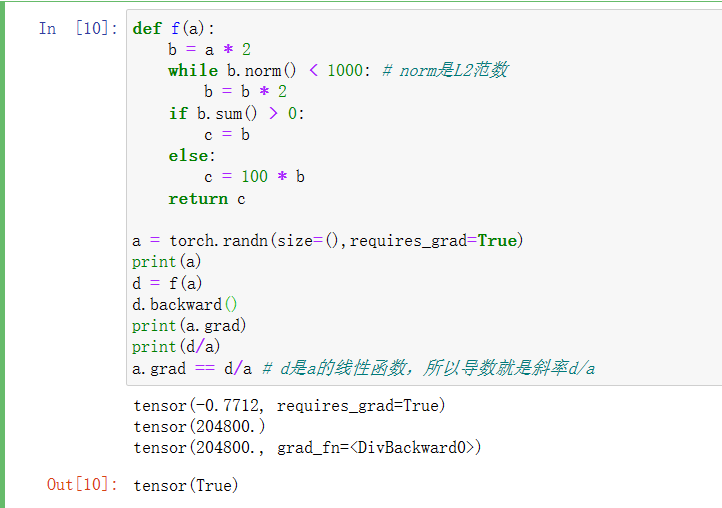
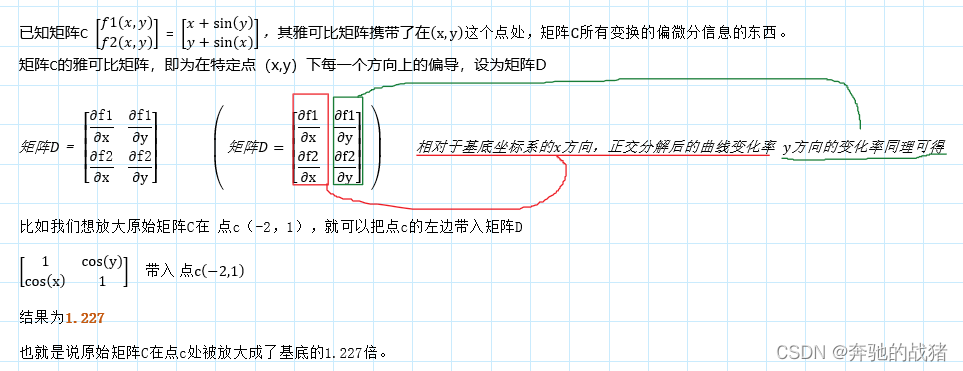

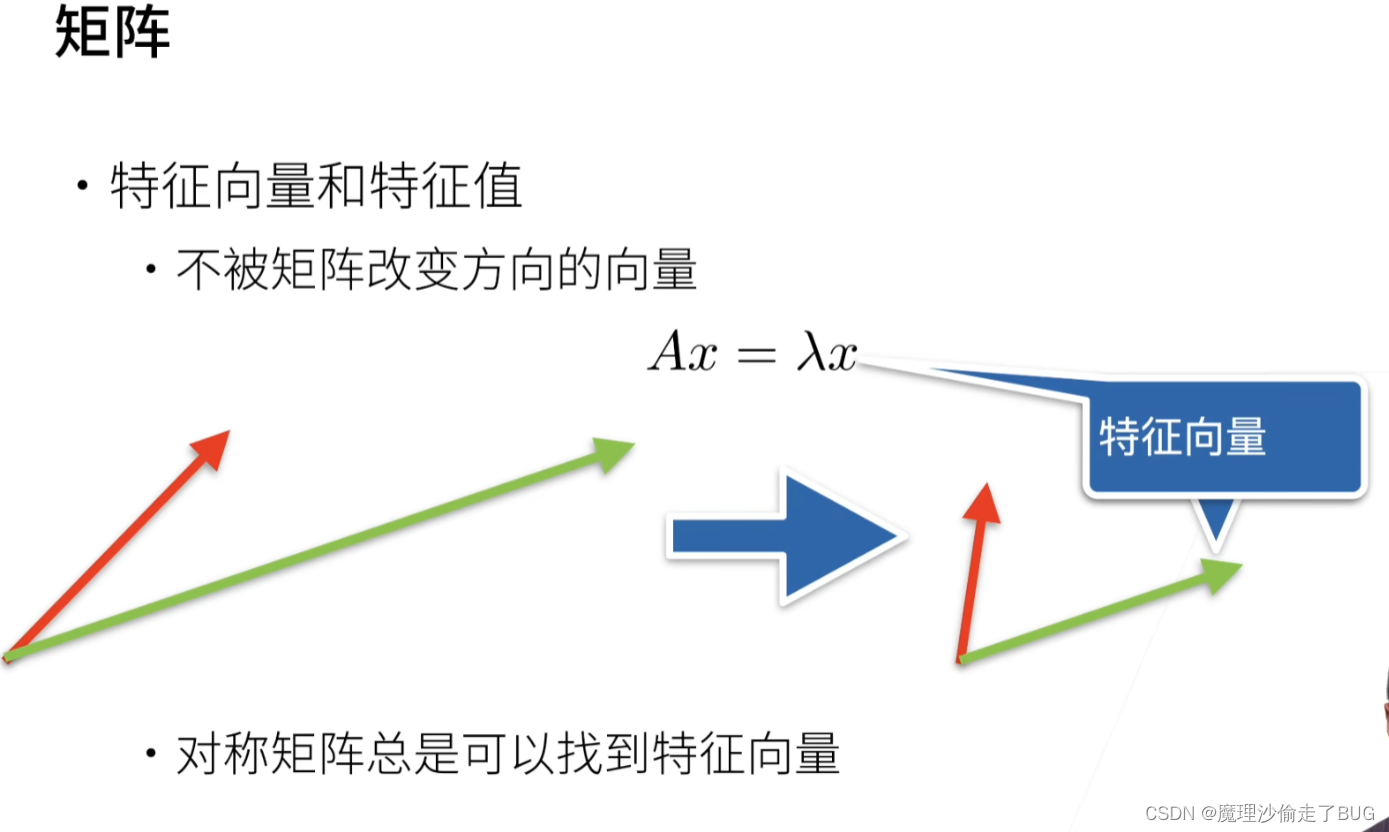

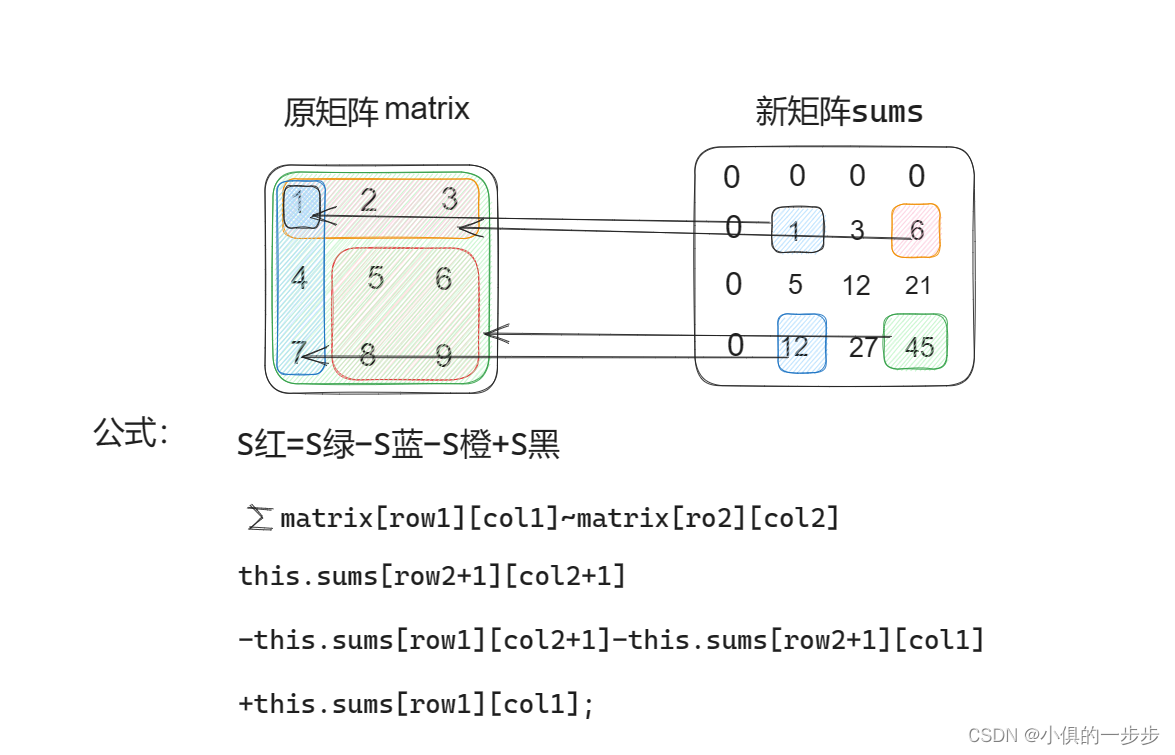
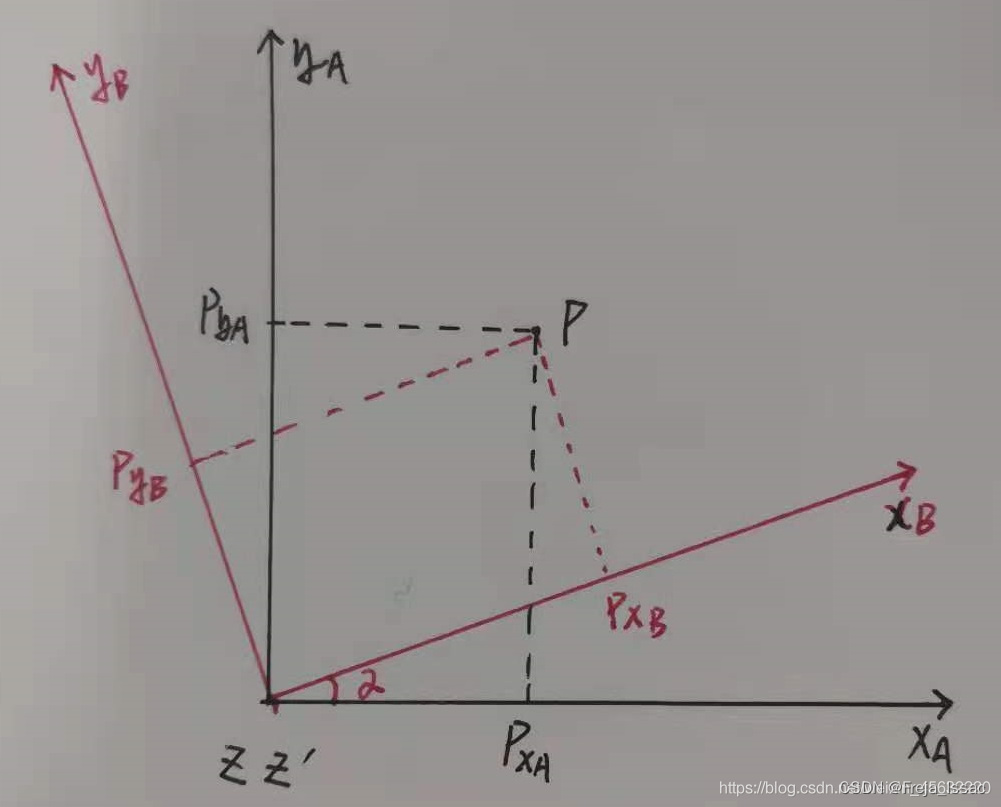
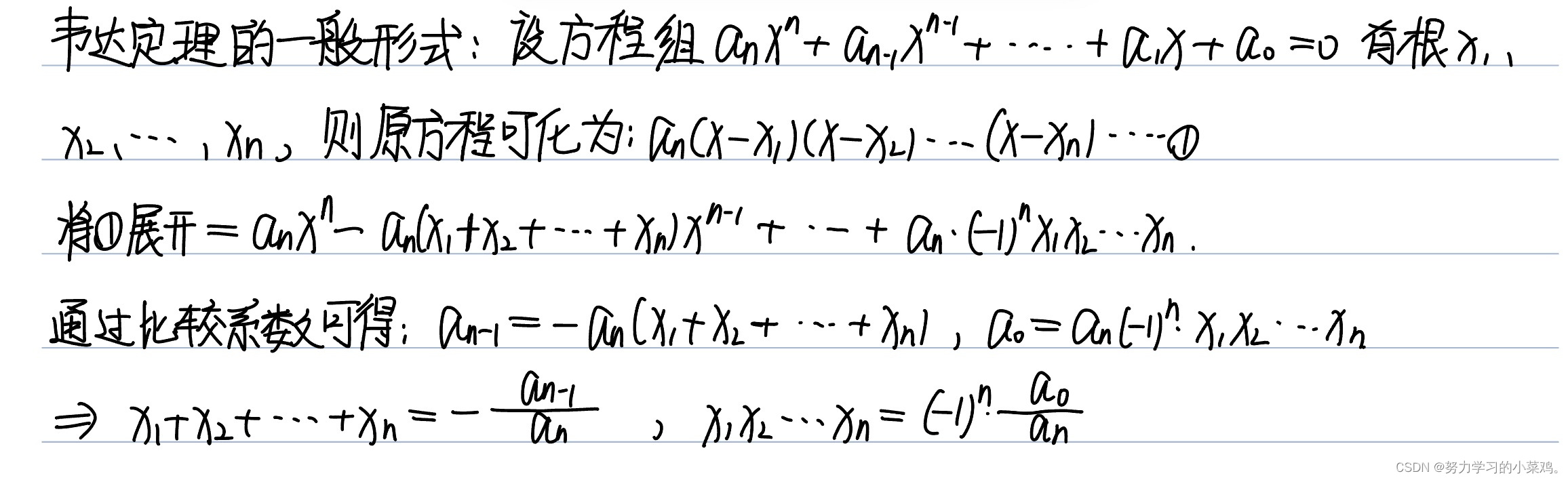
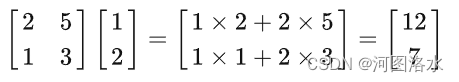
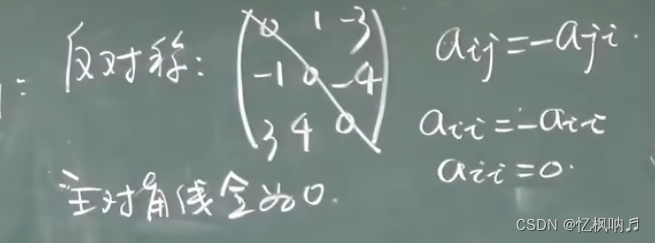
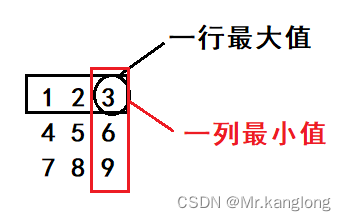
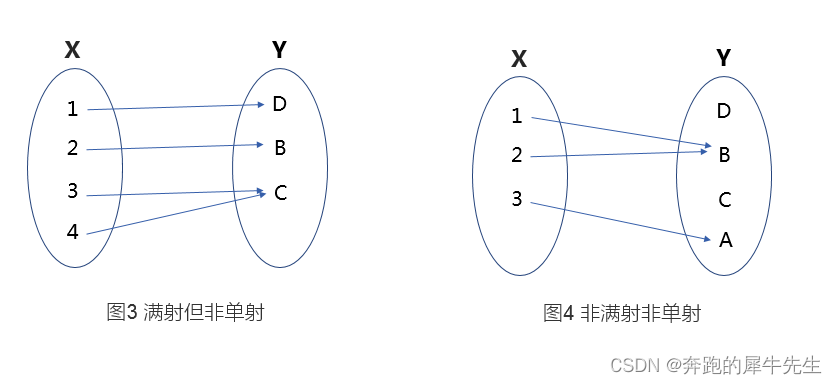

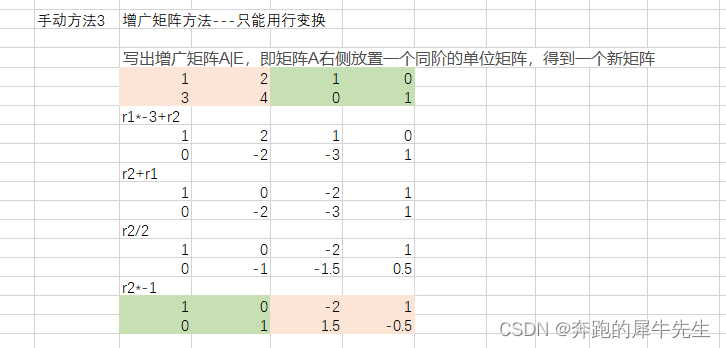
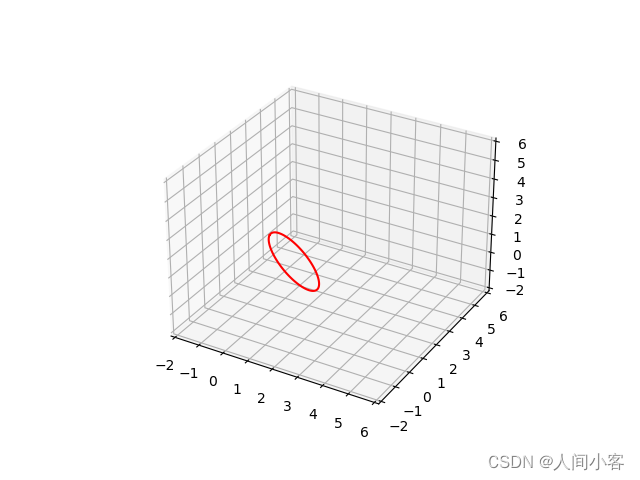
![矩阵快速幂及应用实战[C/C++]](https://img-blog.csdnimg.cn/direct/4984c34723f7415c885992cbce34c118.png)
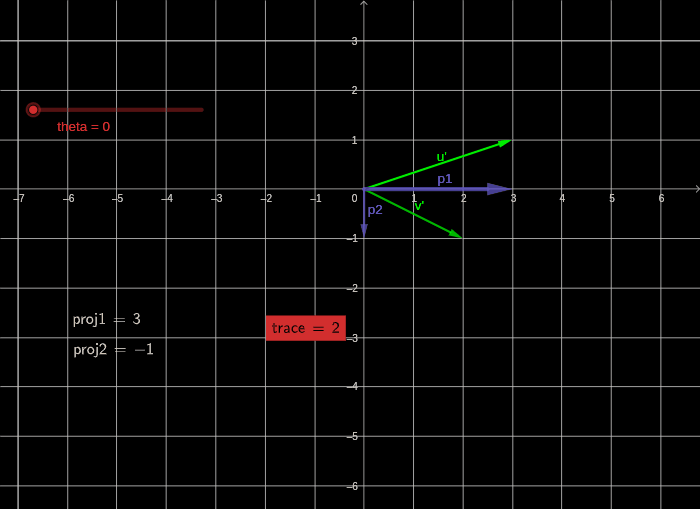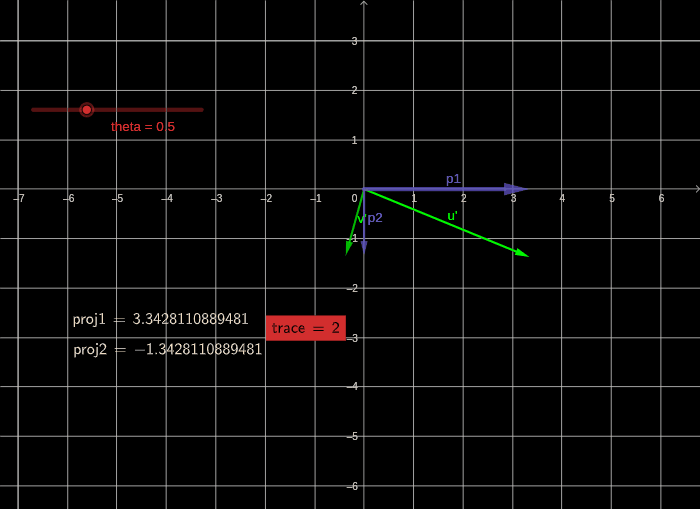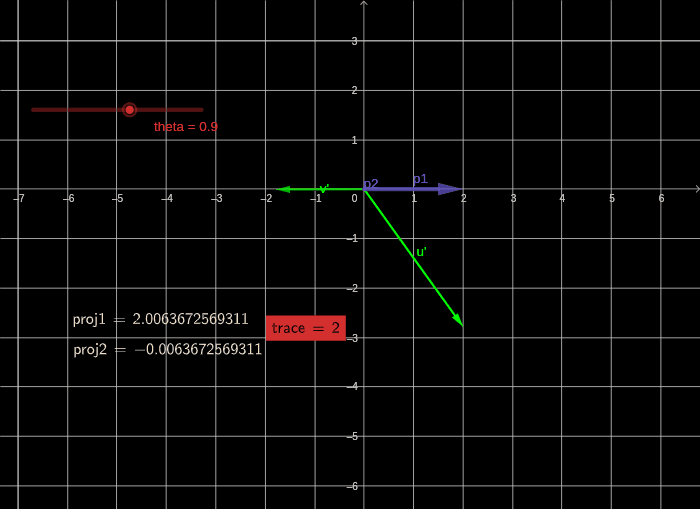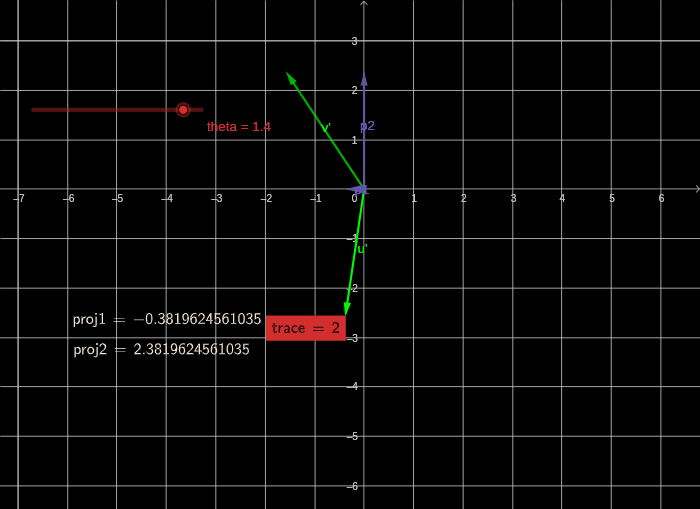

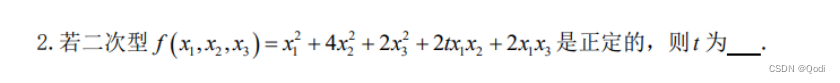
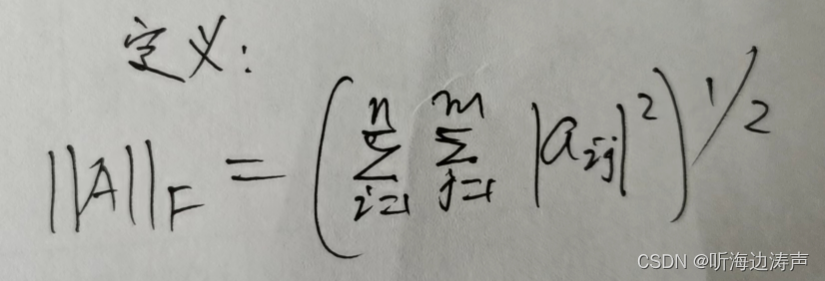
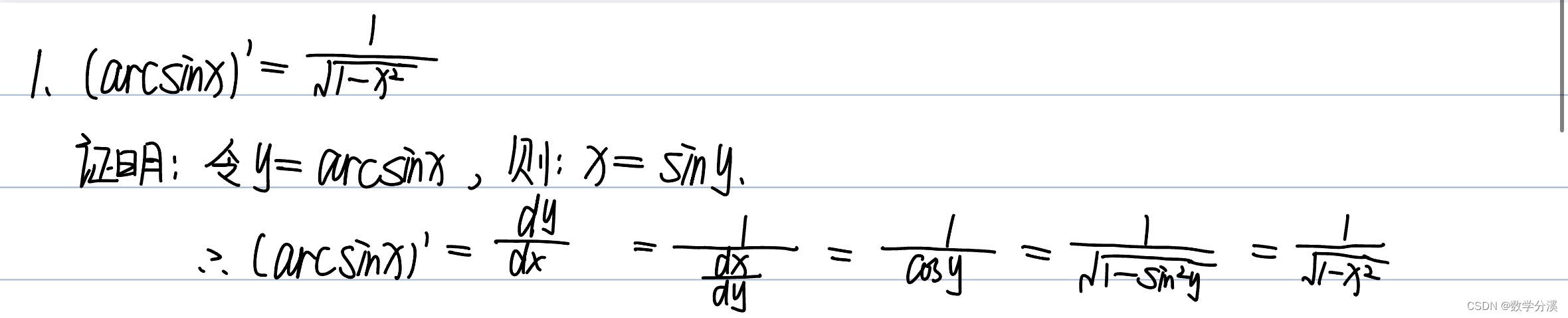
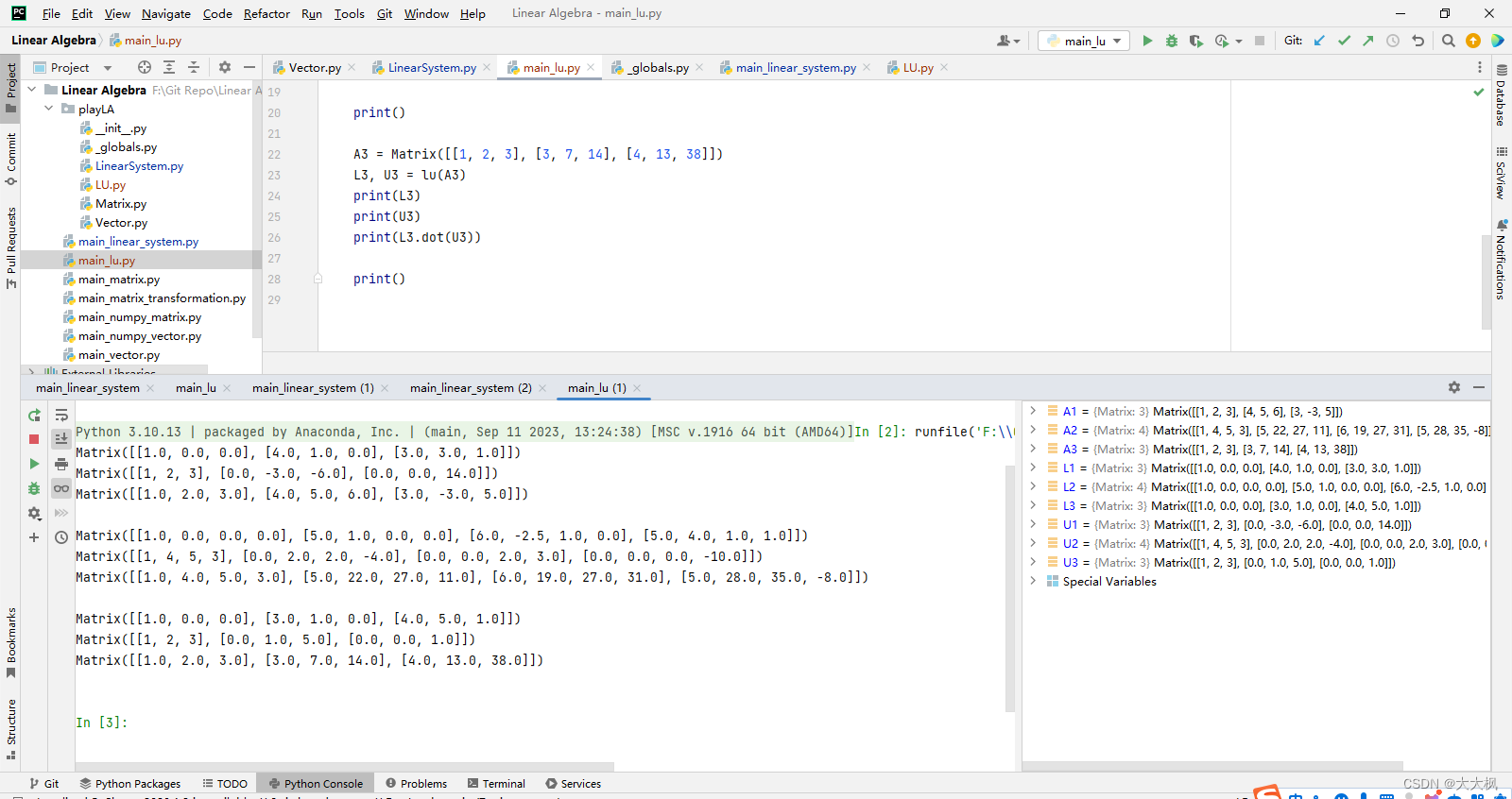
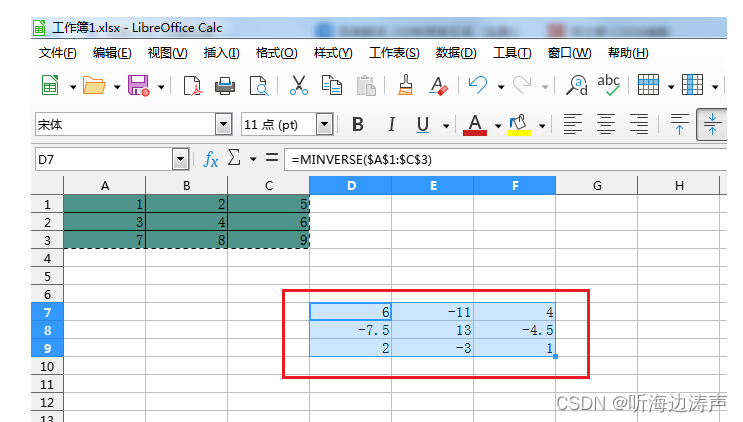
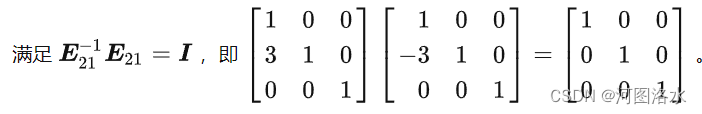








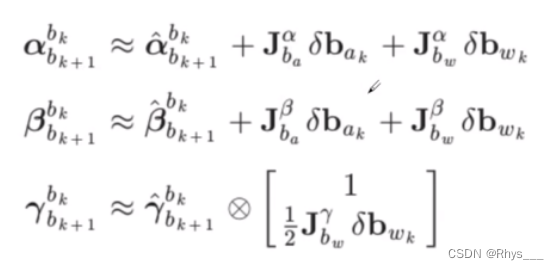


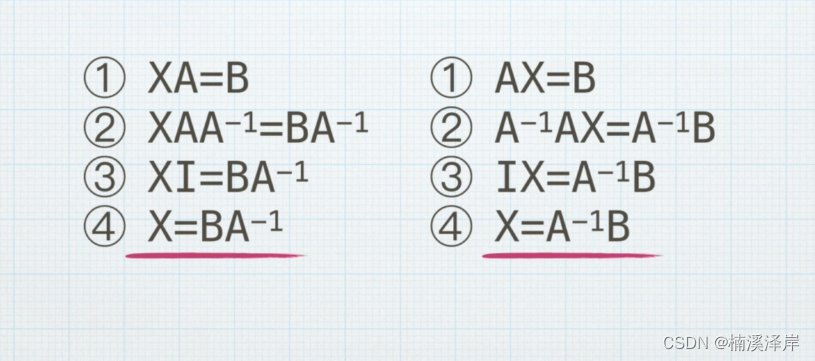
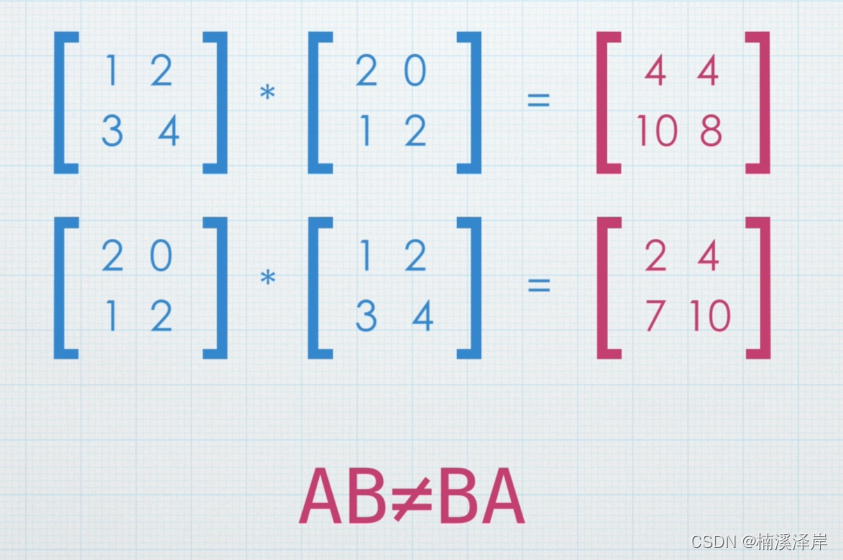














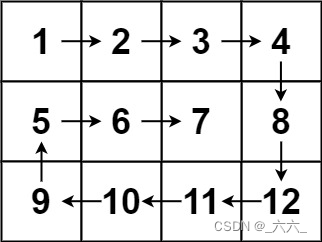







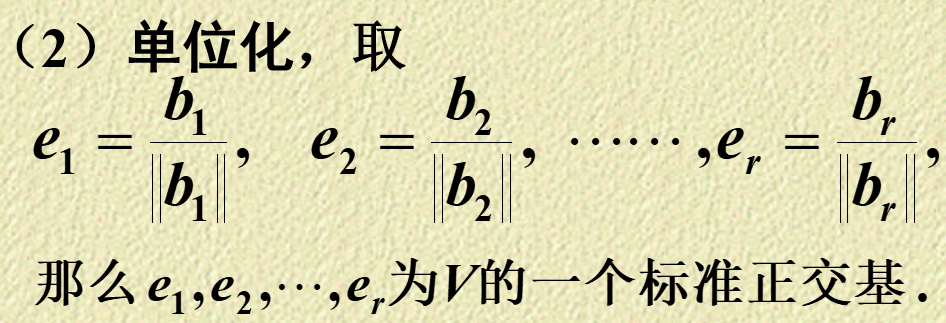
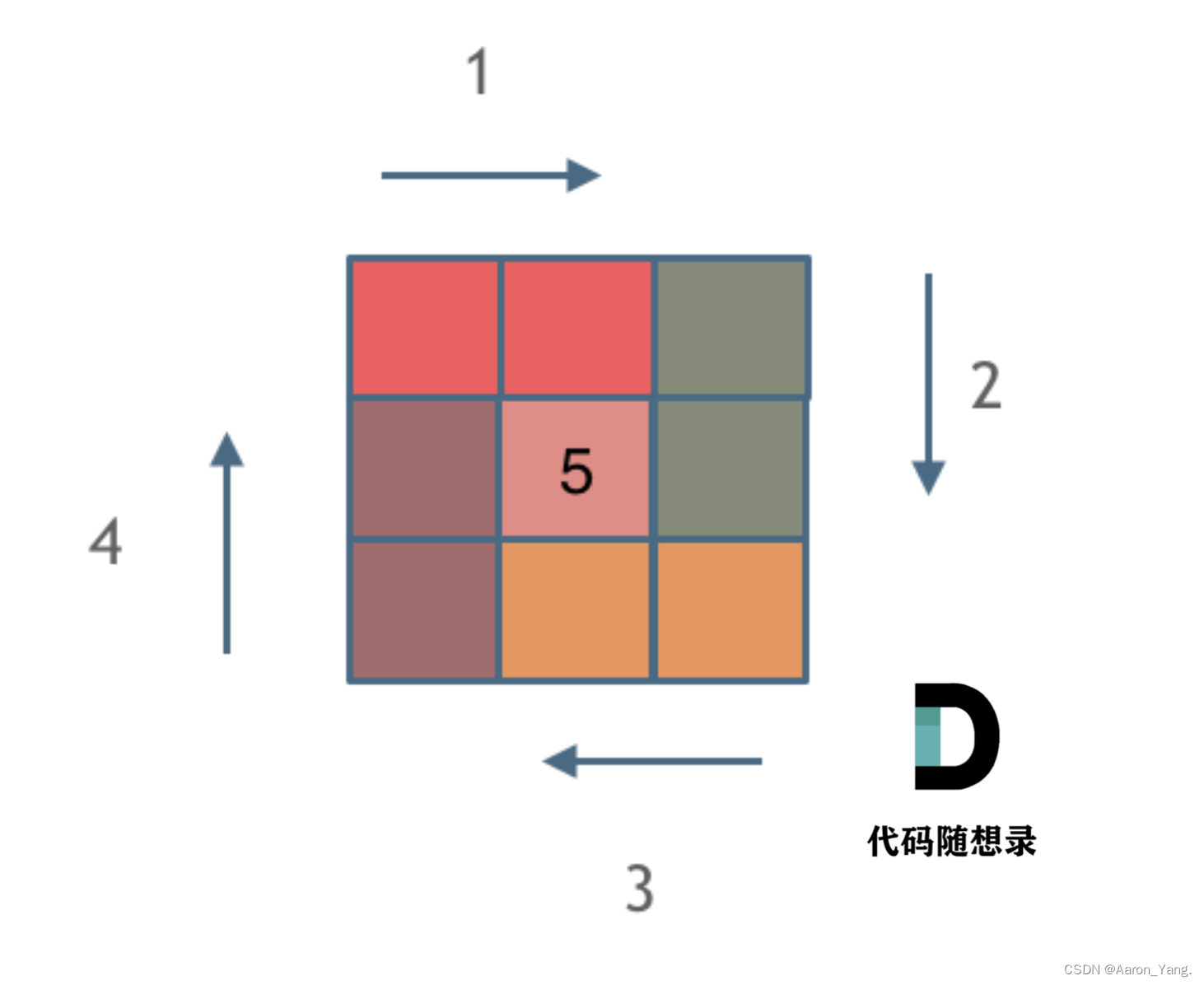

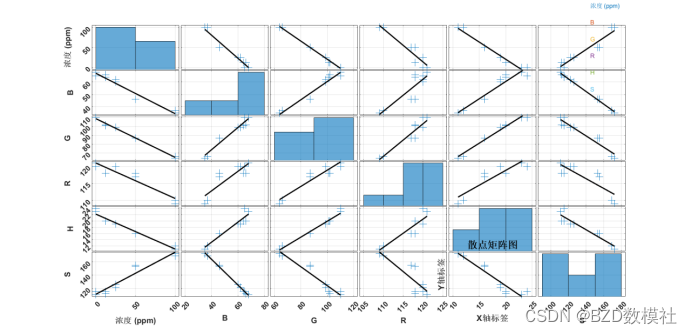



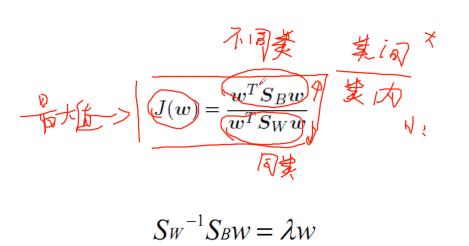


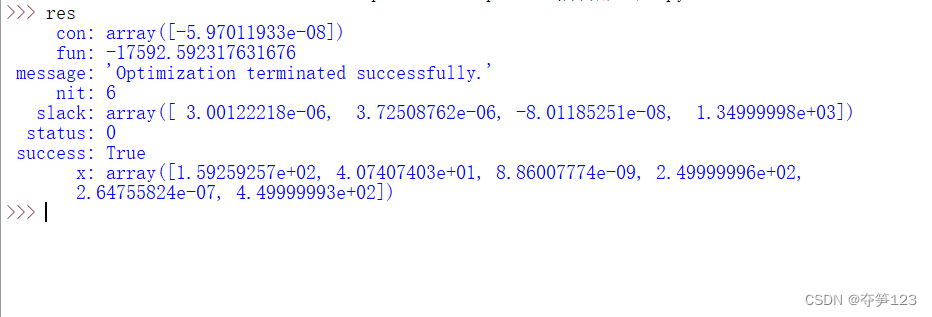

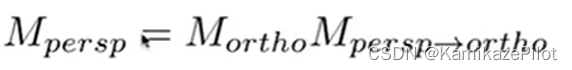
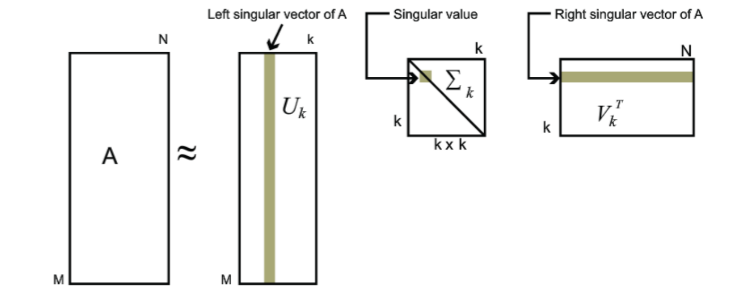




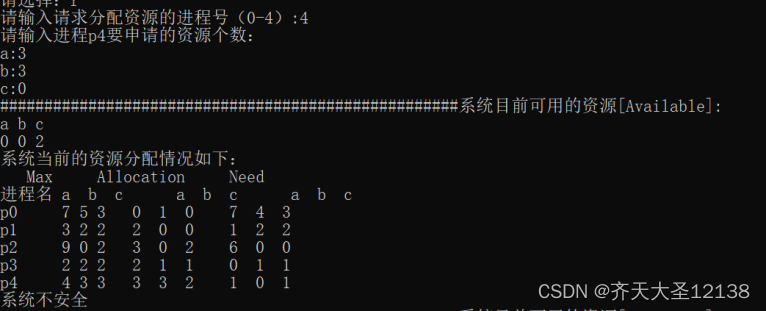
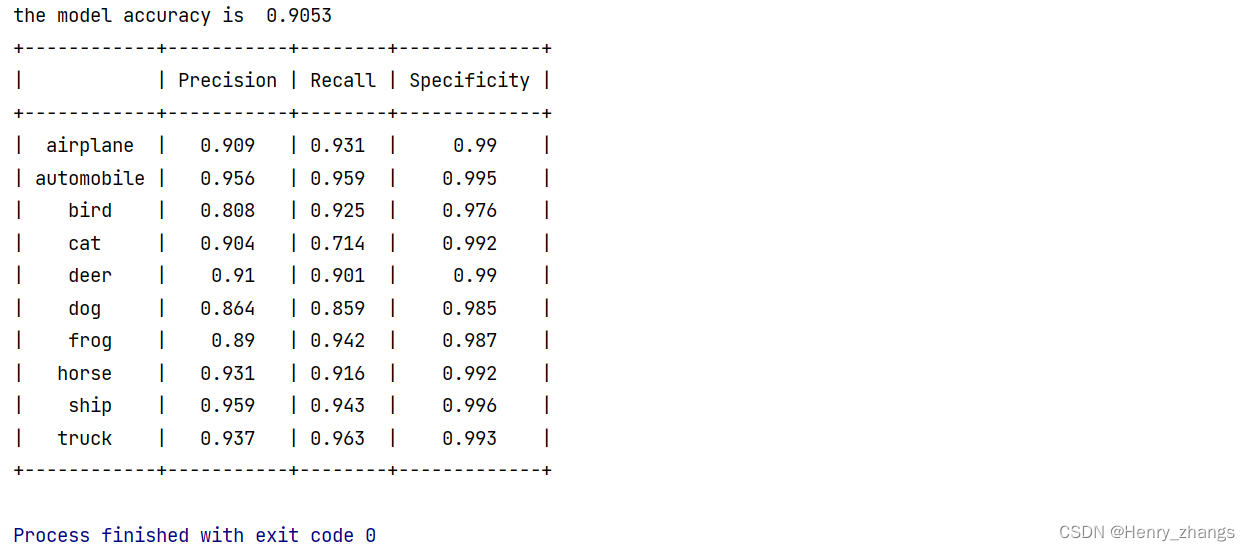



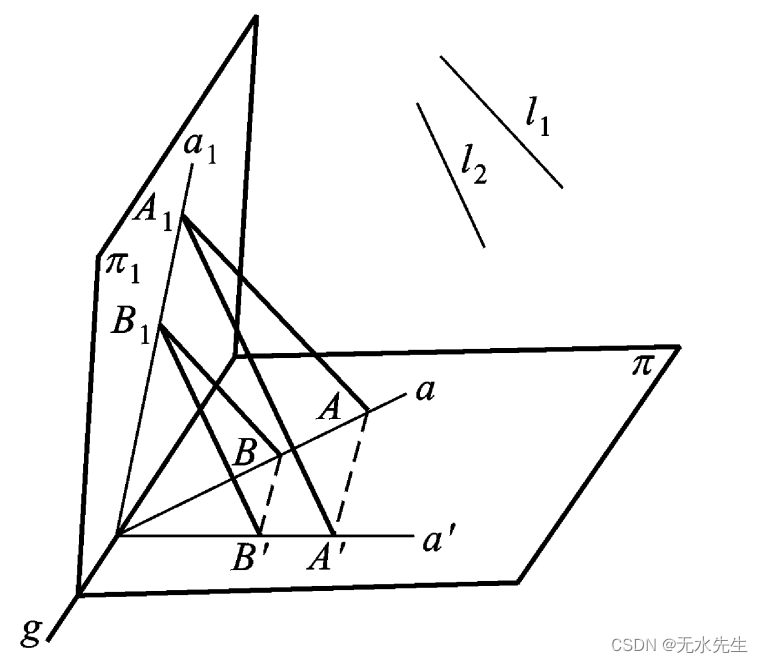


![[Eigen中文文档] 稀疏矩阵操作](https://img-blog.csdnimg.cn/c691a960e075455caab3de3d0fceae45.jpeg#pic_center)


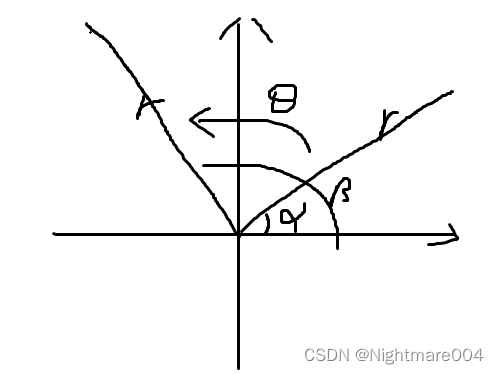









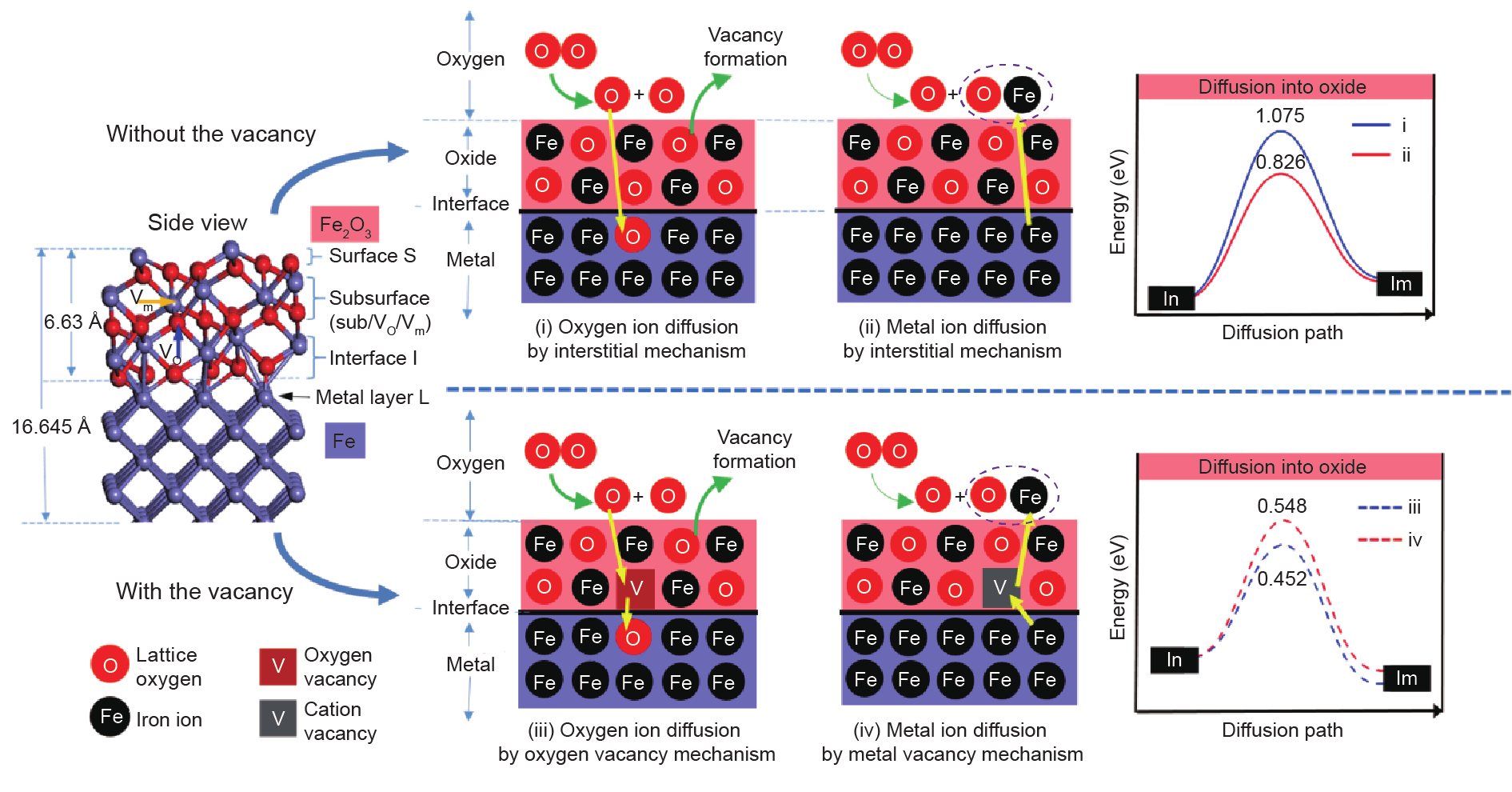



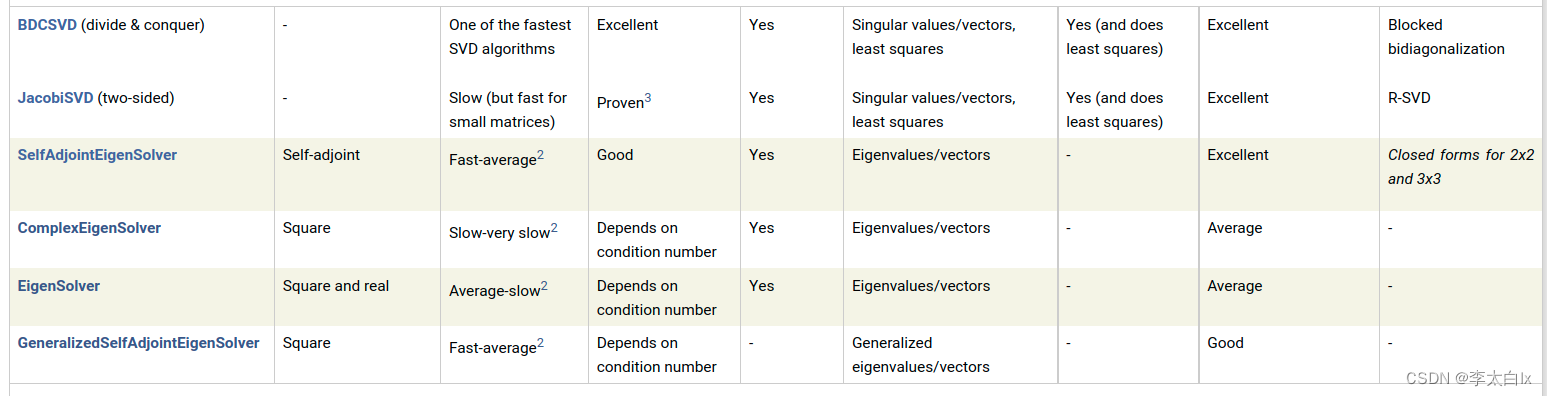
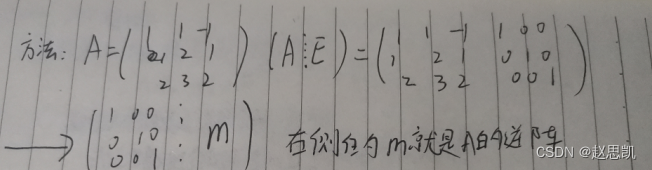


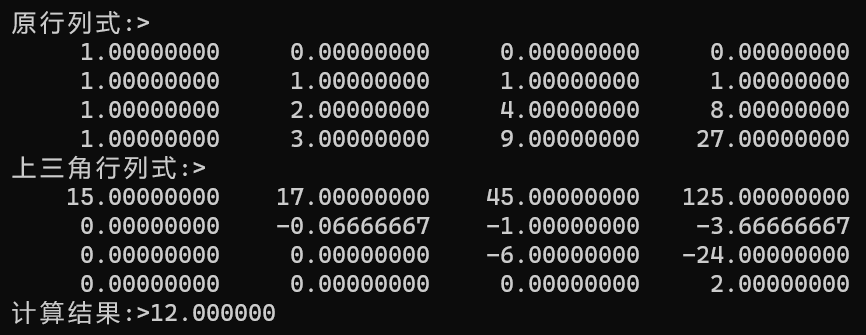








![[现代控制理论]2_state-space状态空间方程](https://img-blog.csdnimg.cn/06f8faa0b32a4ae88802d588d3e85463.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA6LWw5bGx5YGc5rC0,size_20,color_FFFFFF,t_70,g_se,x_16)



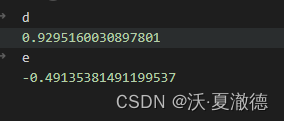




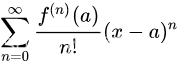

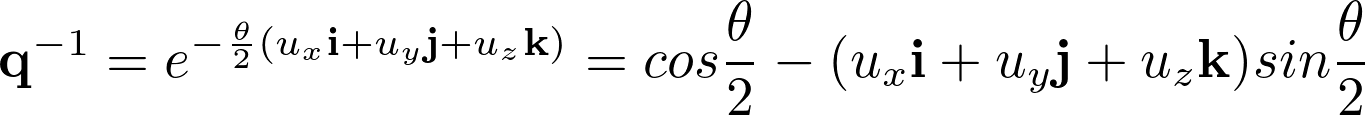


![[解题报告]《算法零基础100讲》(第3讲) 矩阵](https://img-blog.csdnimg.cn/8e9839e1c2fb40e88909946b0720f862.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAWGluZ2xlaUdhbw==,size_20,color_FFFFFF,t_70,g_se,x_16)
![[现代控制理论]9_状态观测器设计_龙伯格观测器](https://img-blog.csdnimg.cn/6a84503febaf4194937d93b7b2cc0a25.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA546L5bSH5Y2r,size_20,color_FFFFFF,t_70,g_se,x_16)











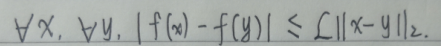




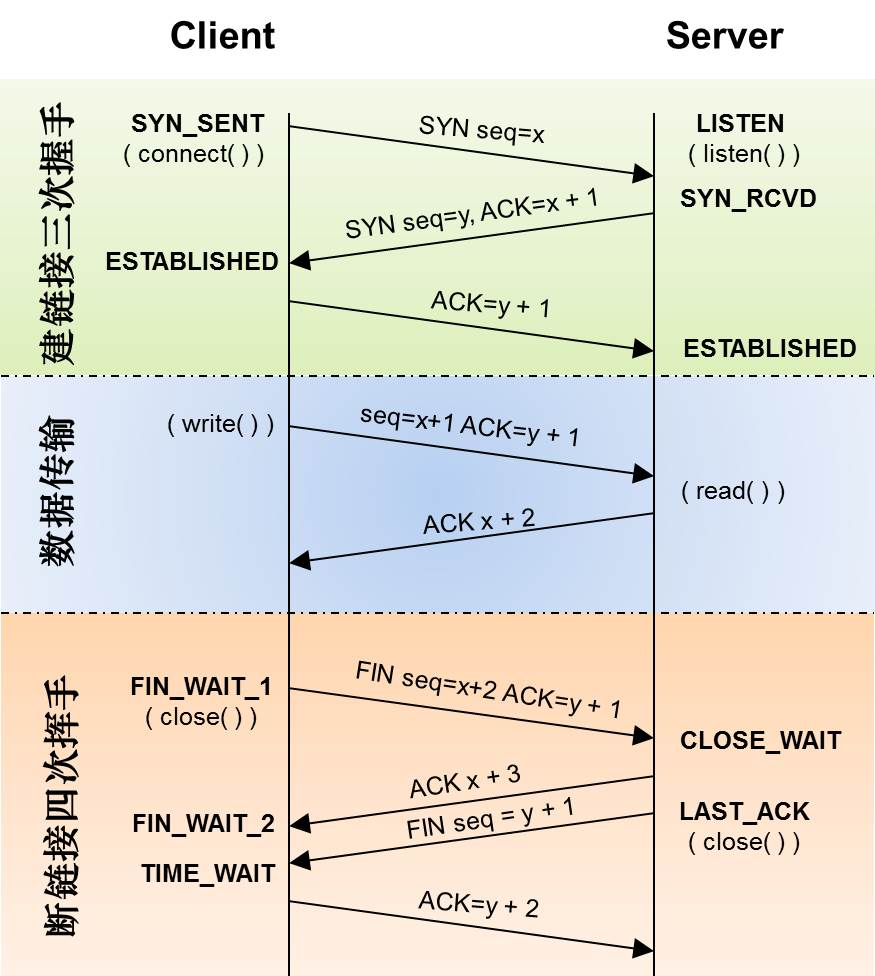




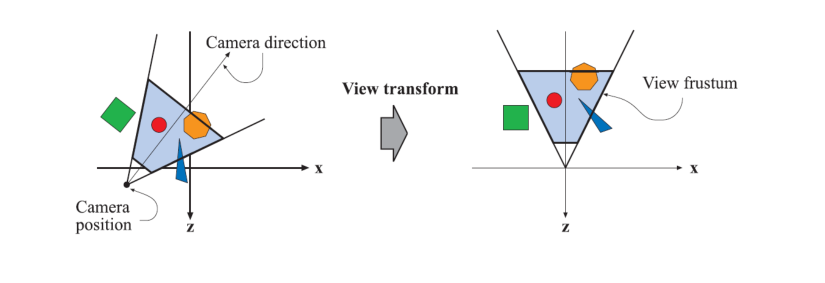



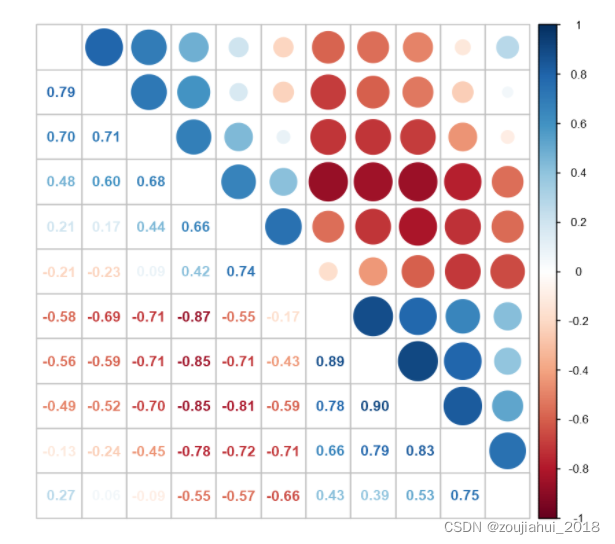
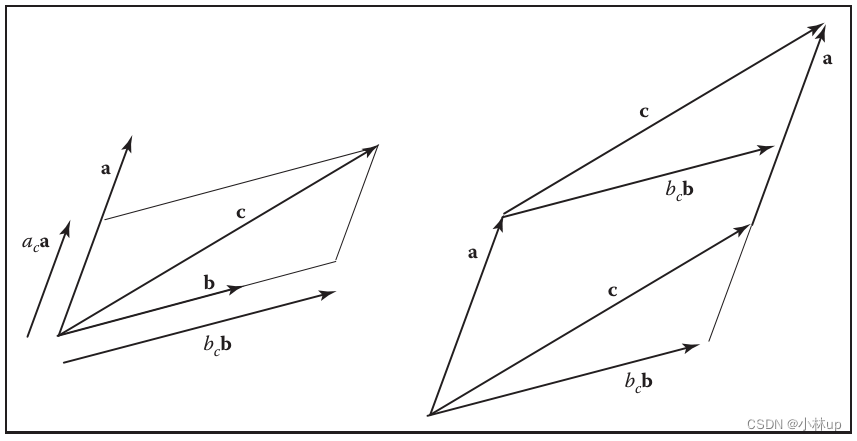






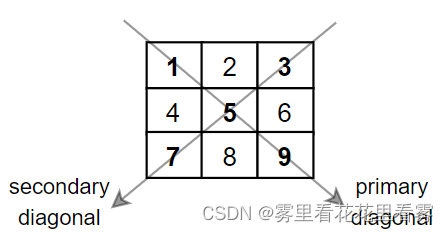


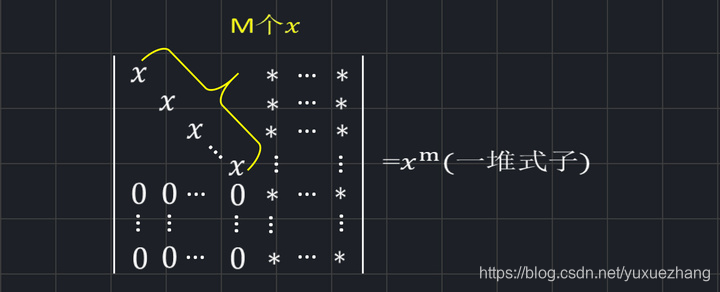





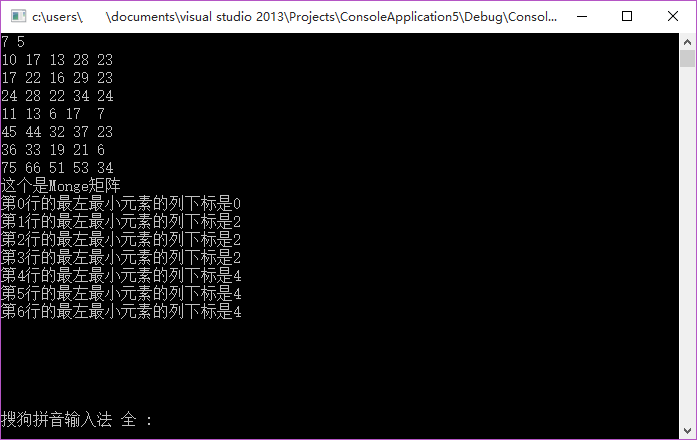
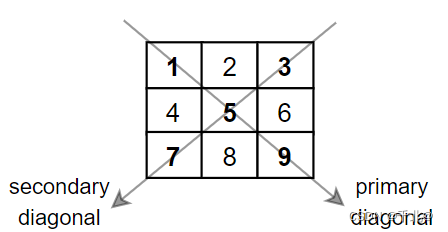
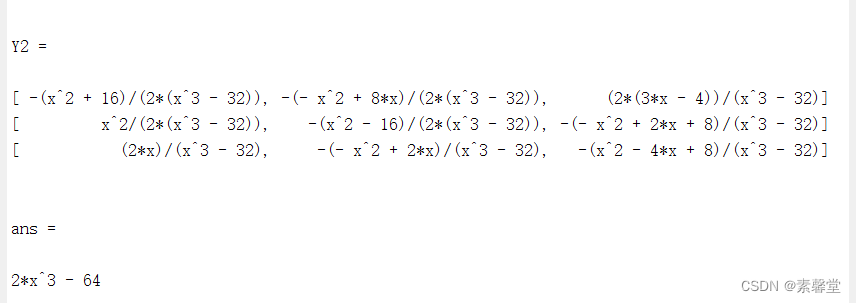
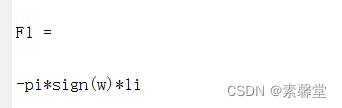


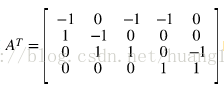














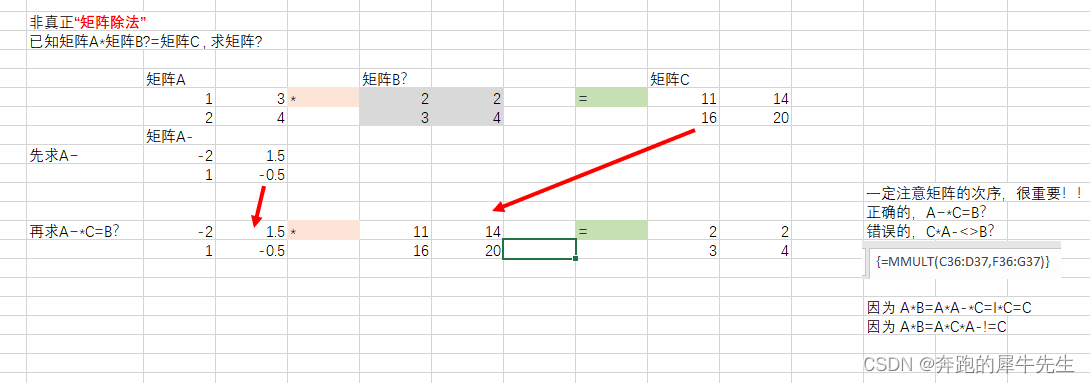
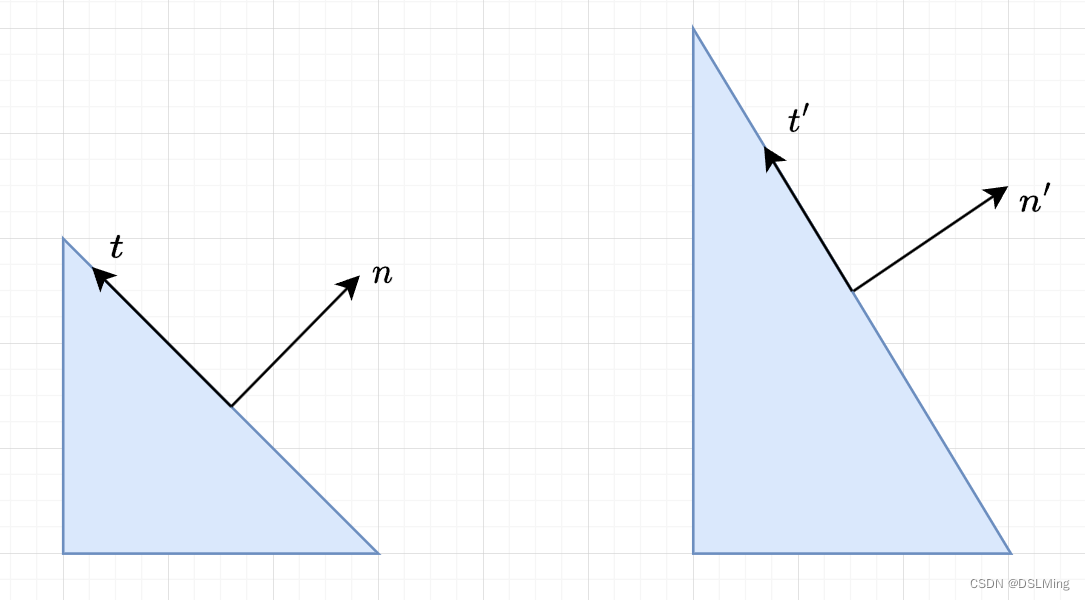

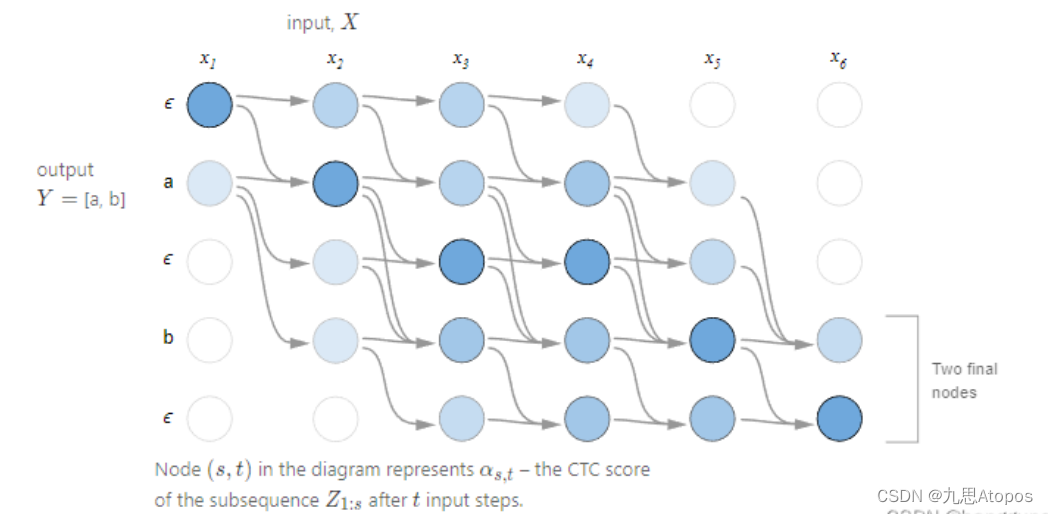




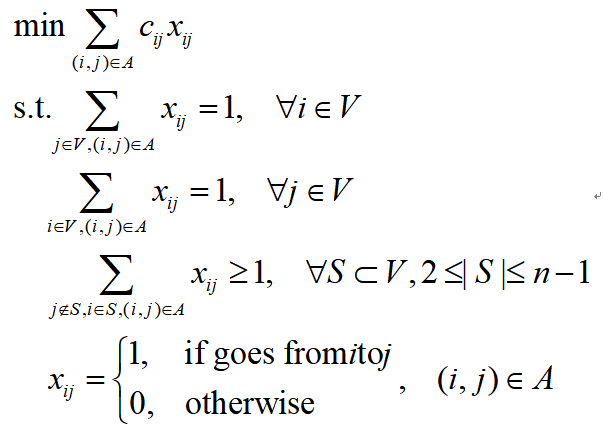



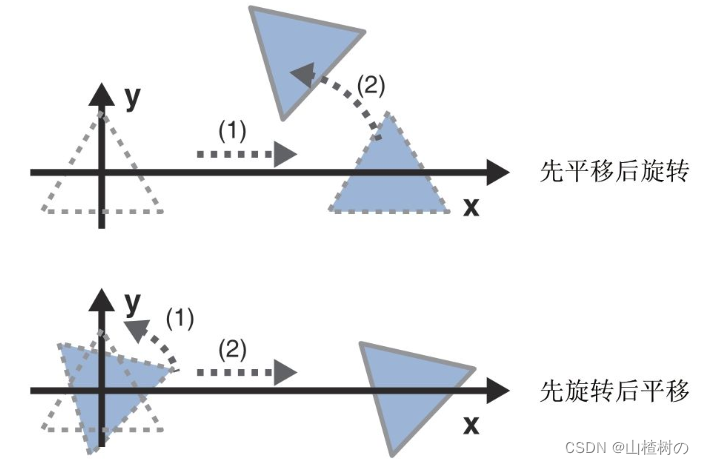
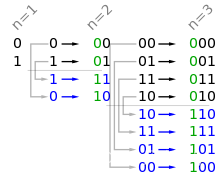



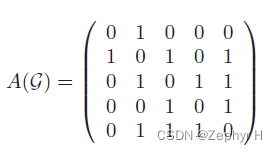
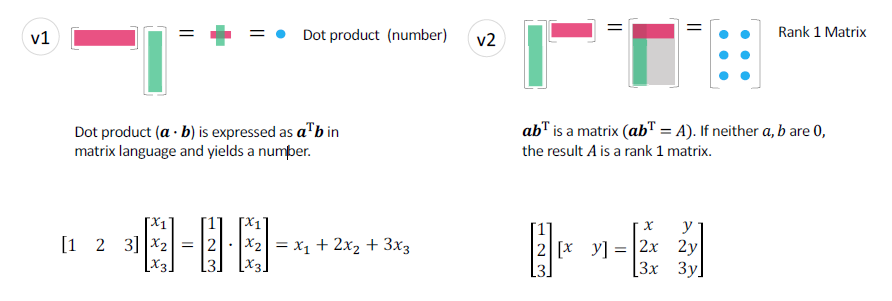
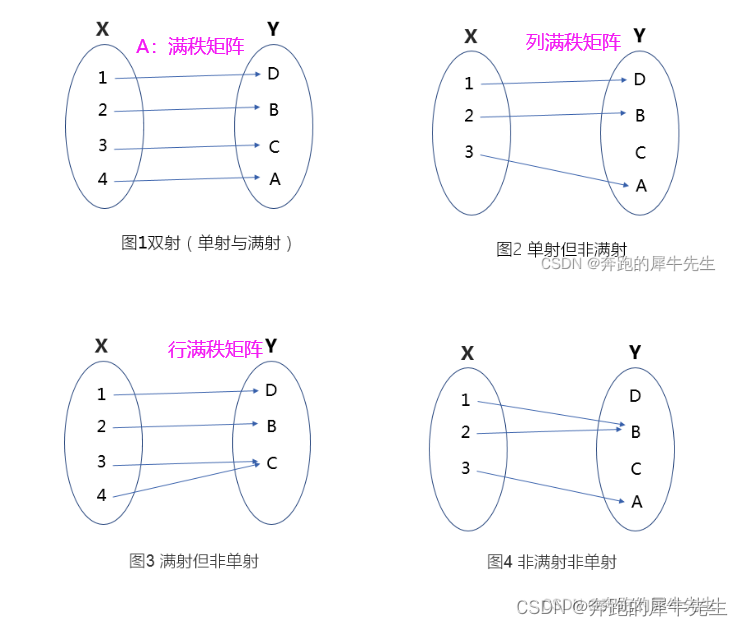



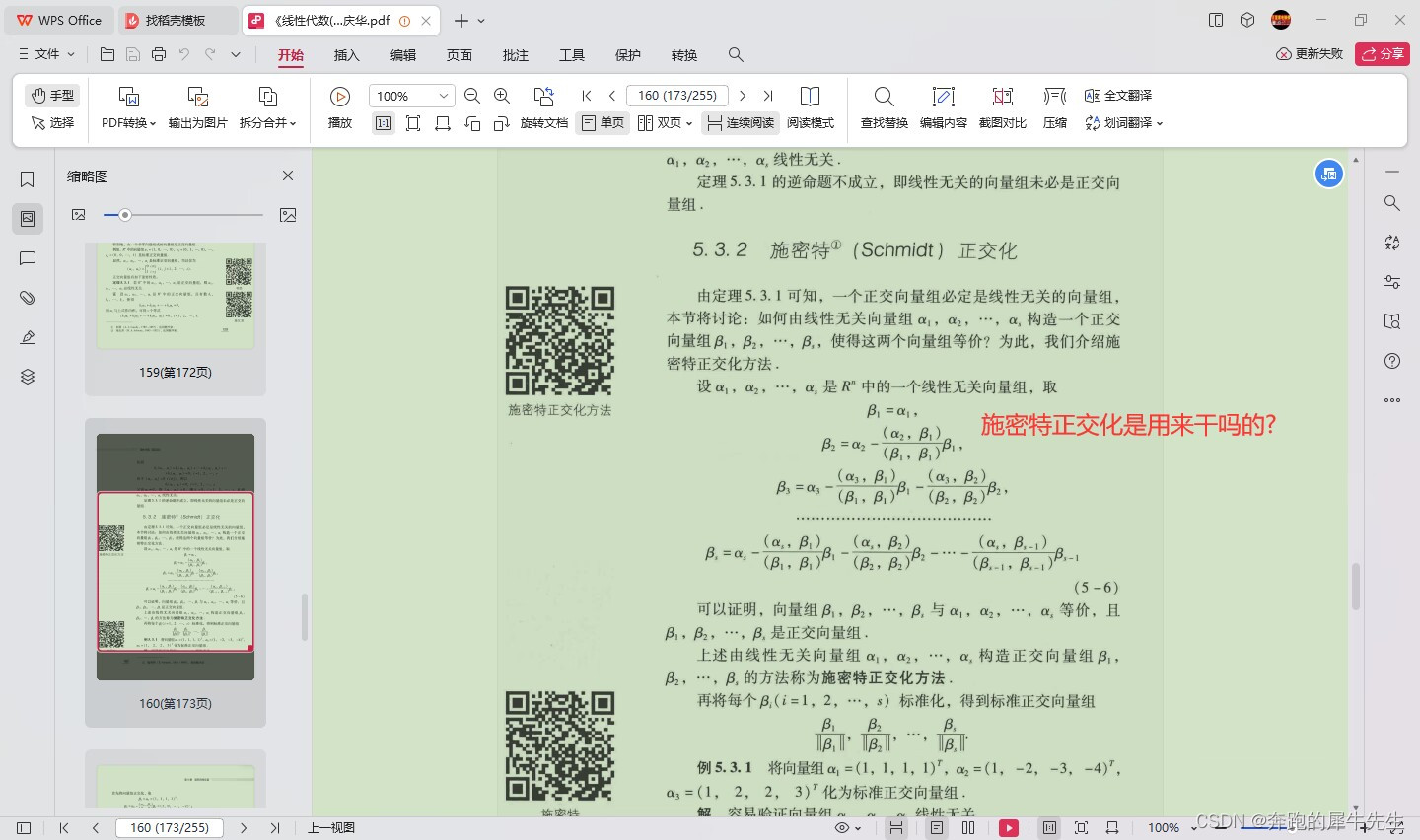

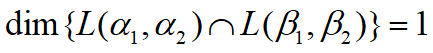











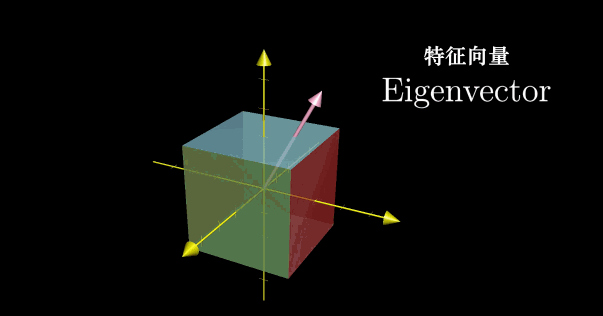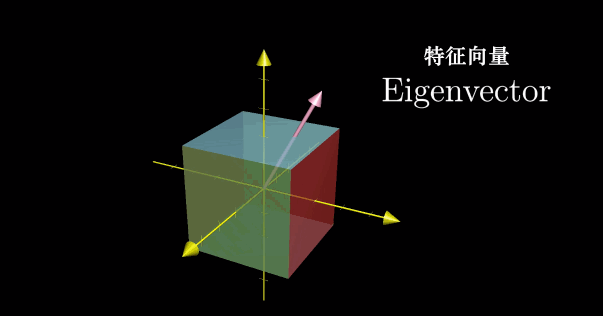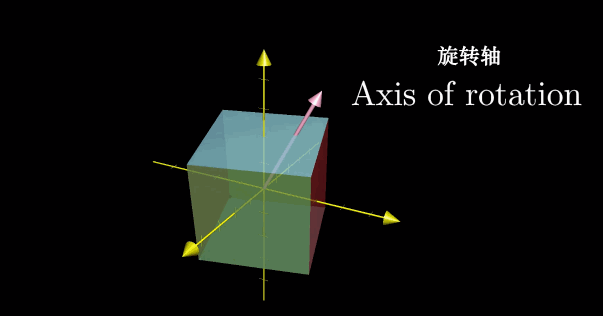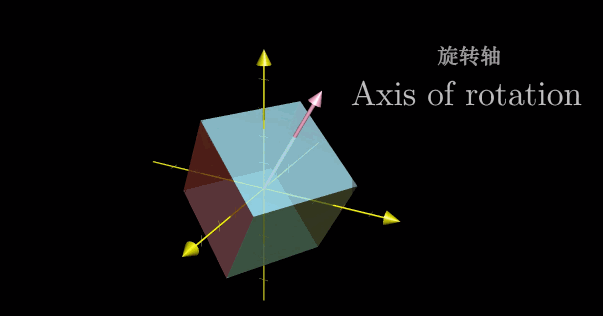
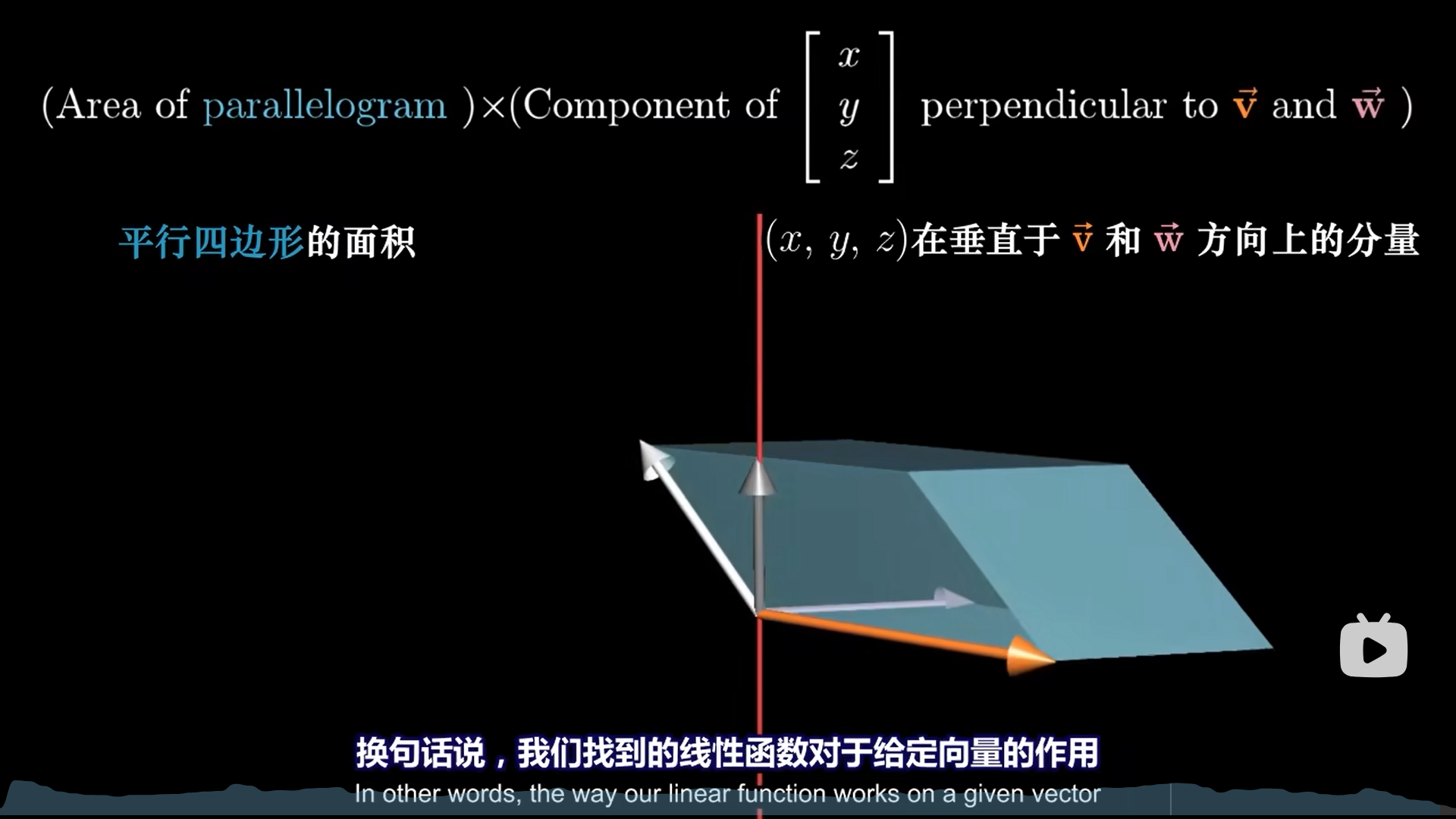
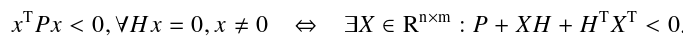





![[02] Multi-sensor KIT: DSP 矩阵运算-加法,减法和逆矩阵,放缩,乘法和转置矩阵](https://img-blog.csdnimg.cn/5bdb682377664789b177f9edfffe3542.png)


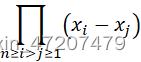


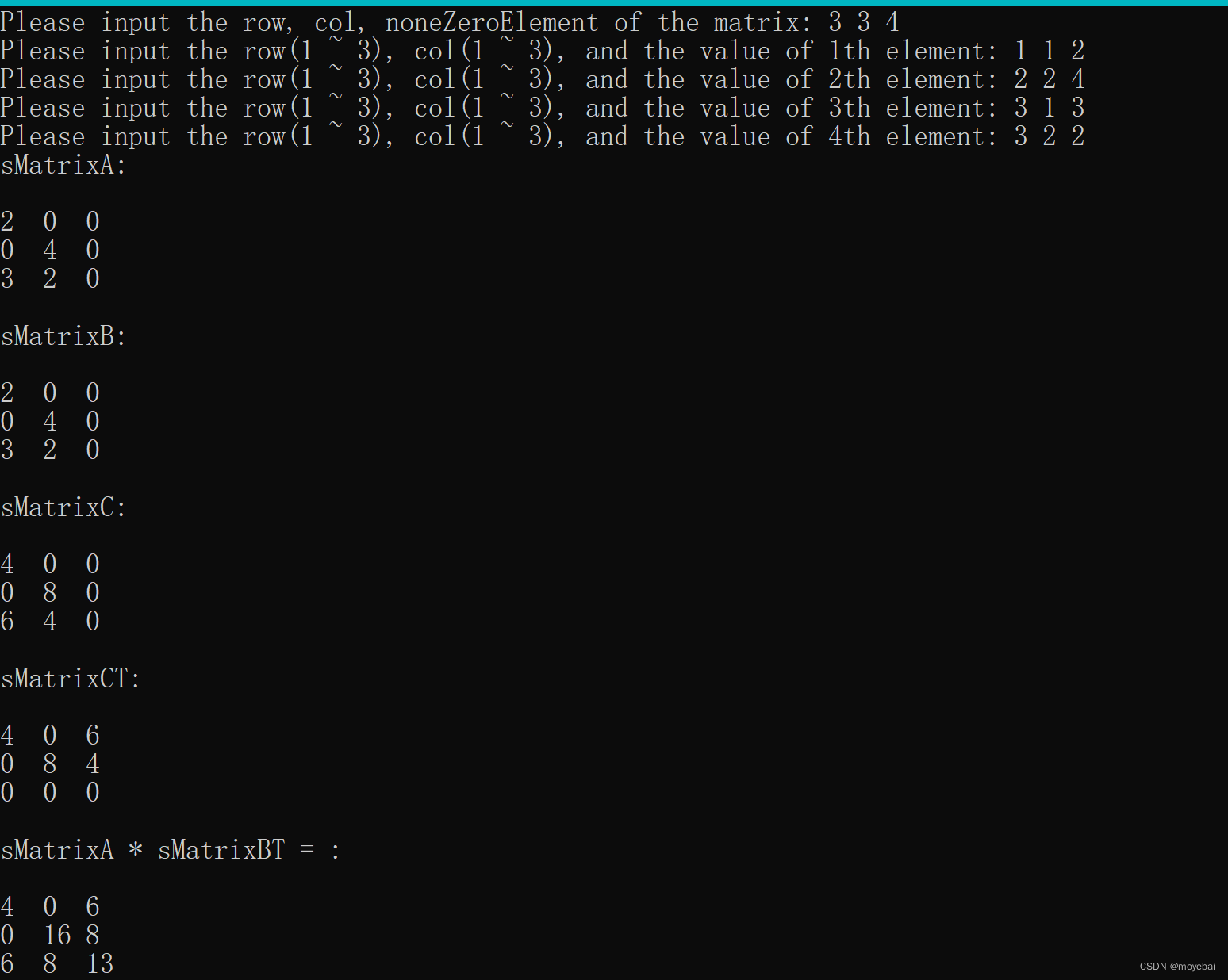









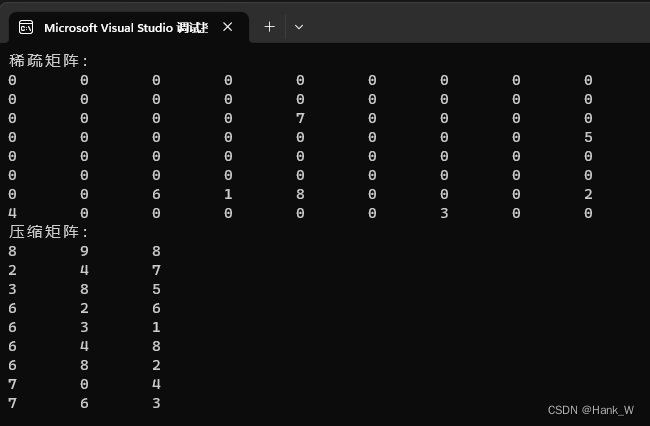
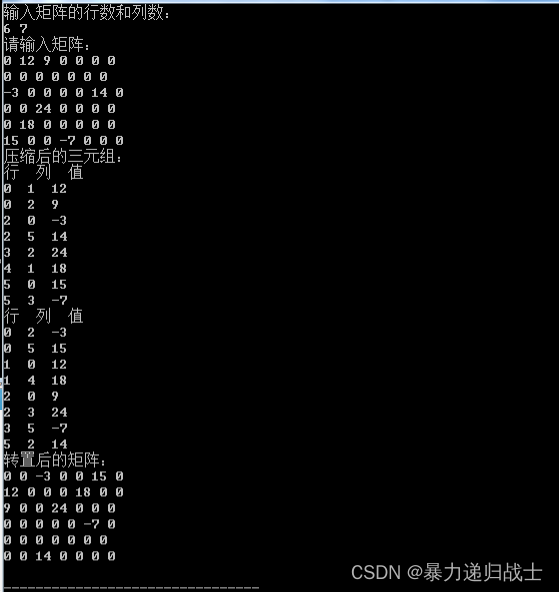
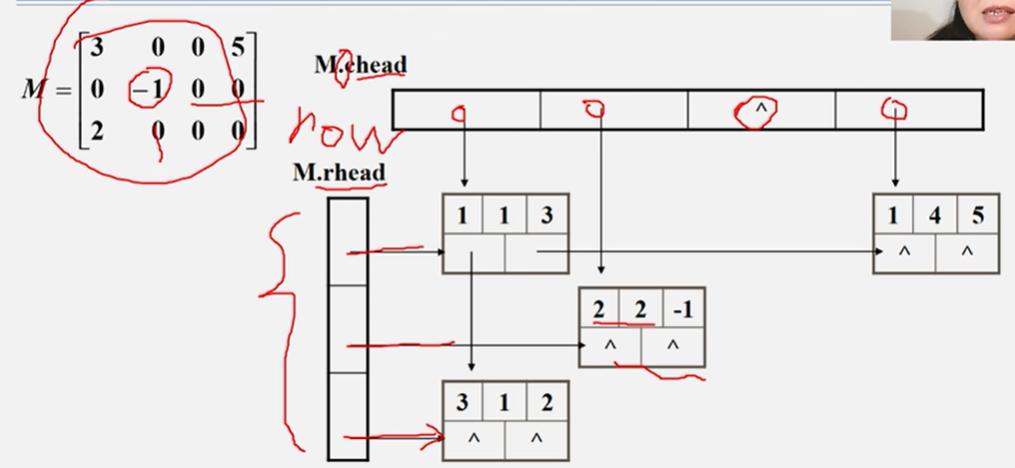



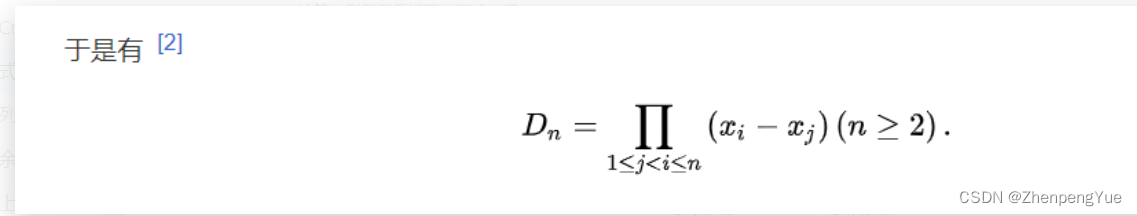






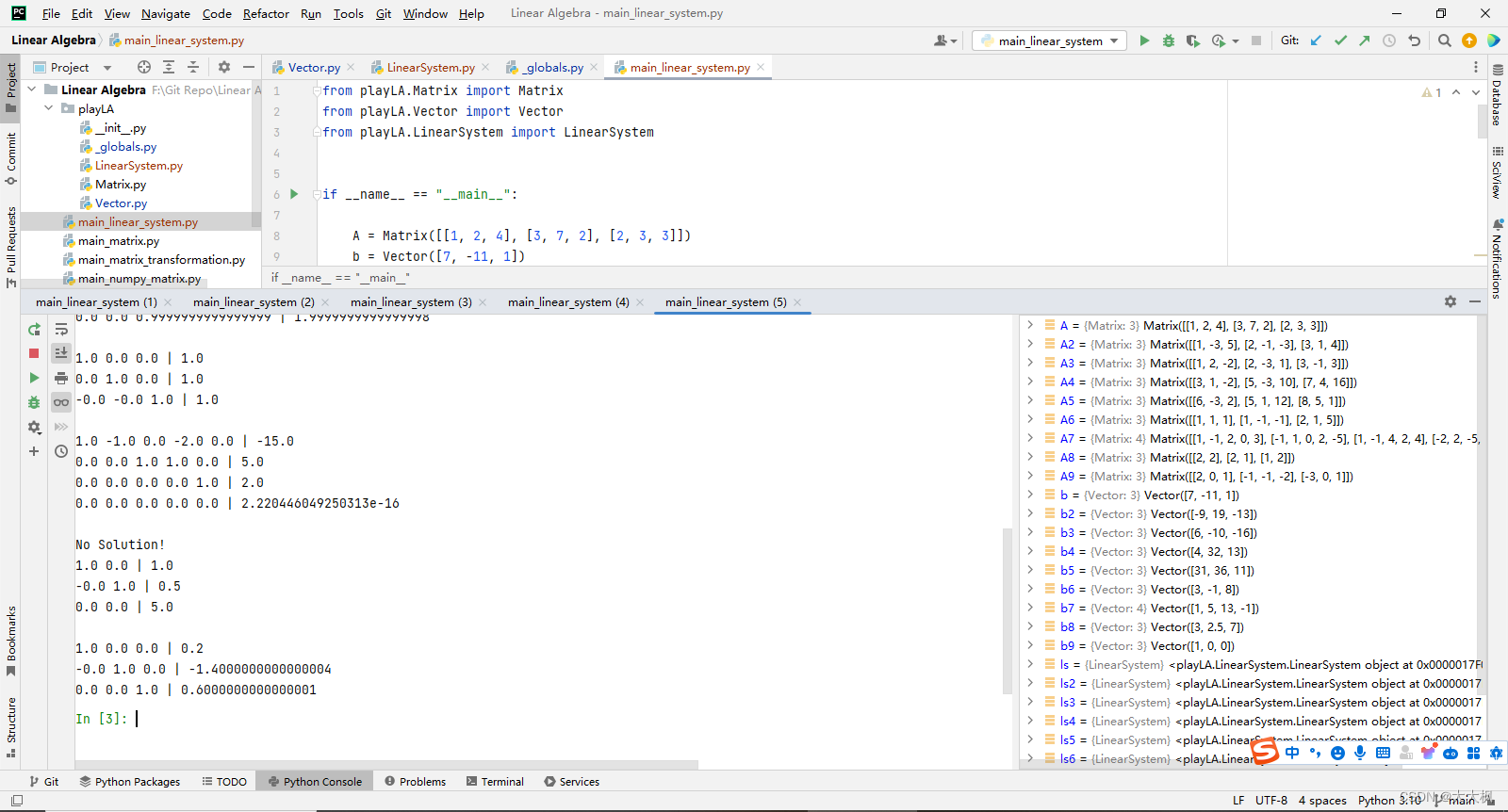

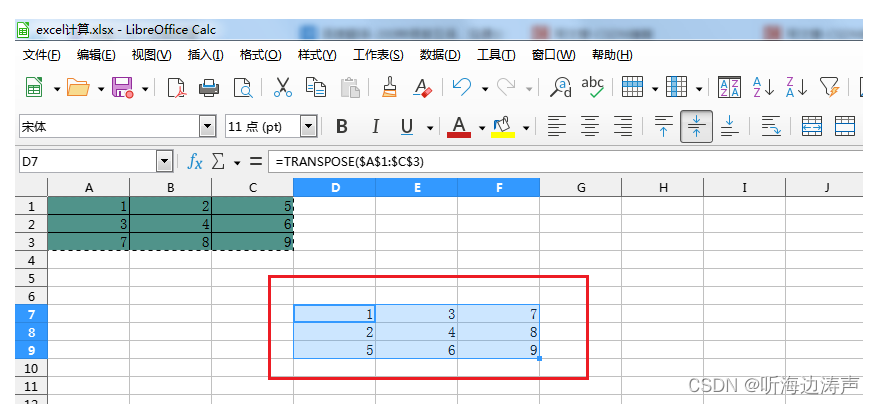
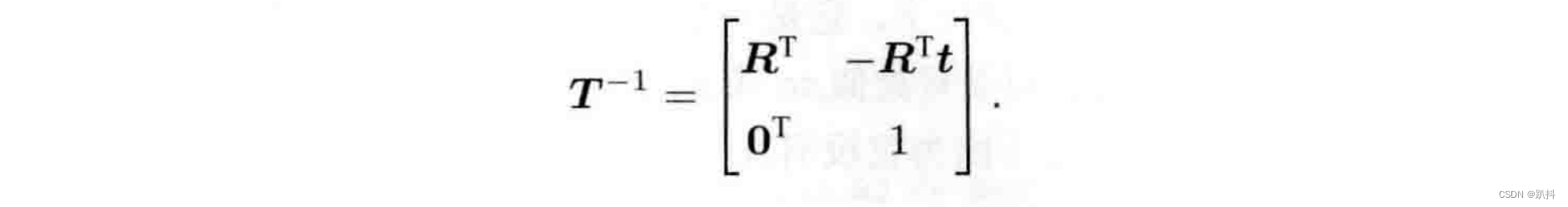



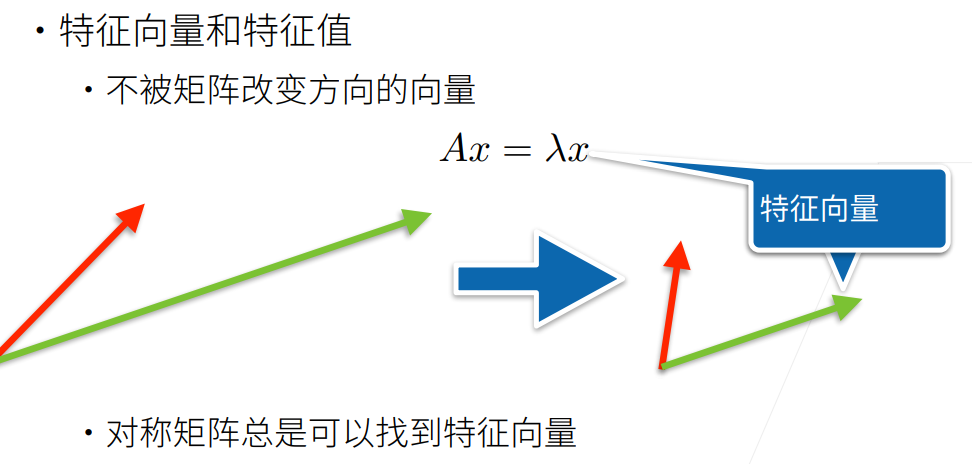

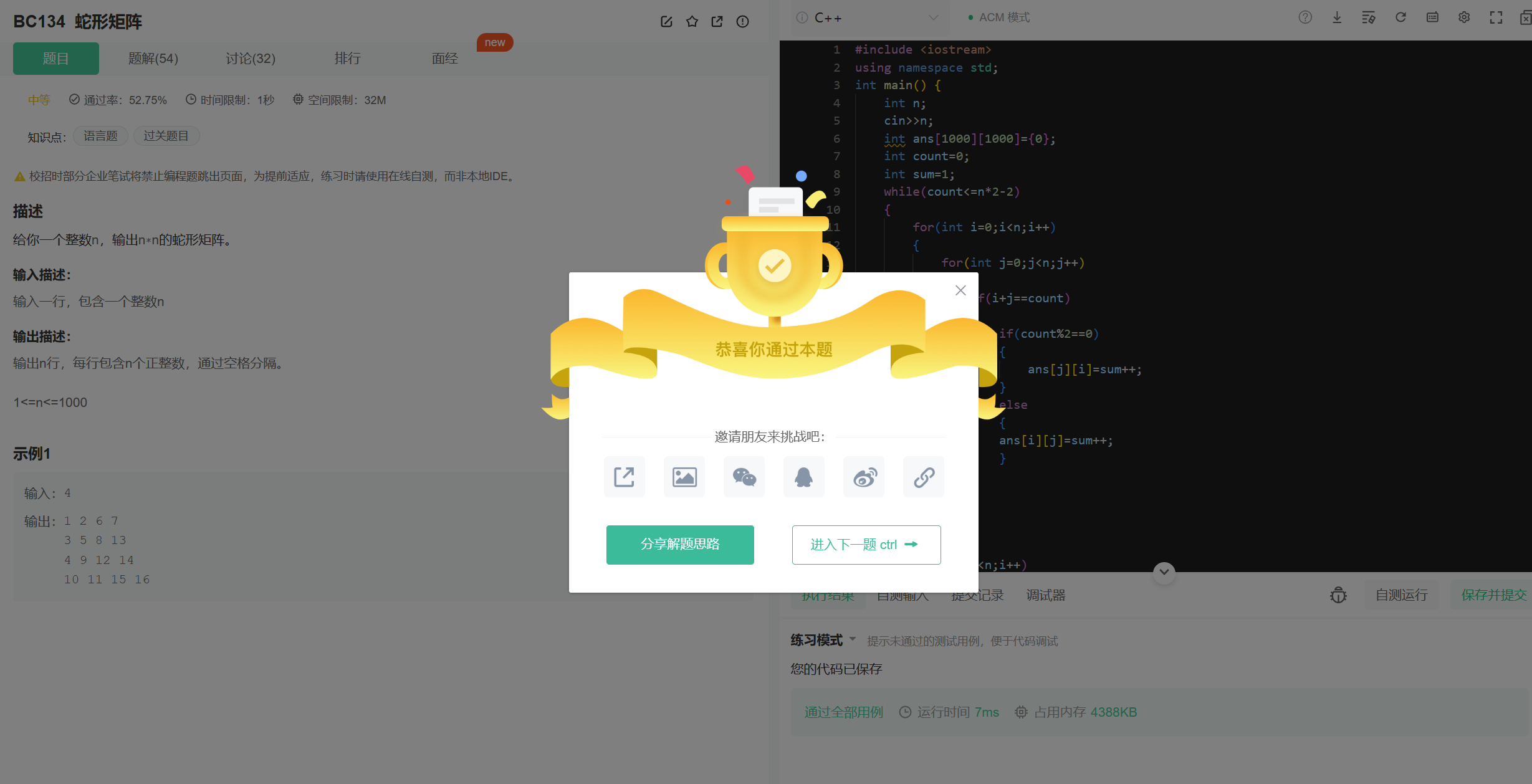

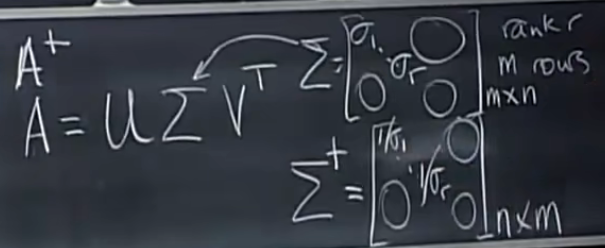



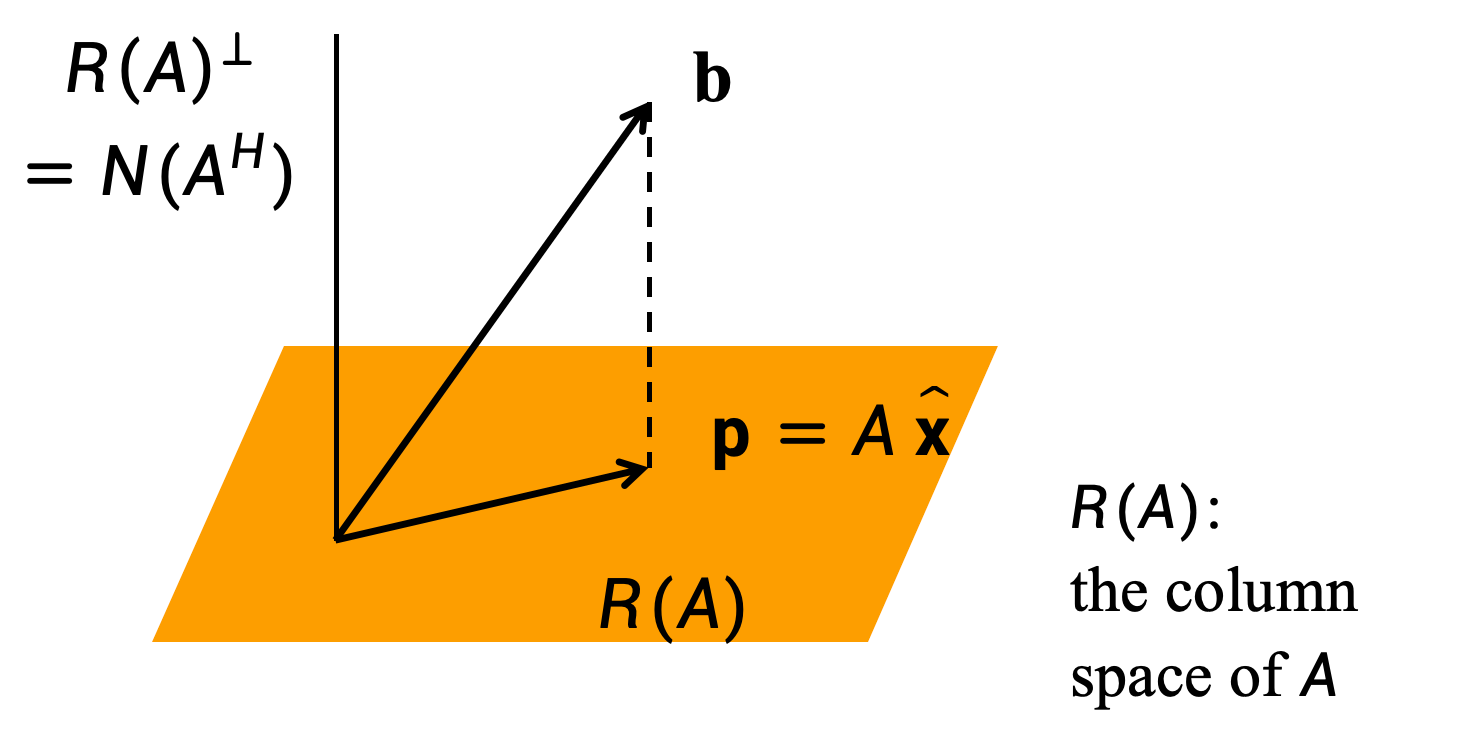
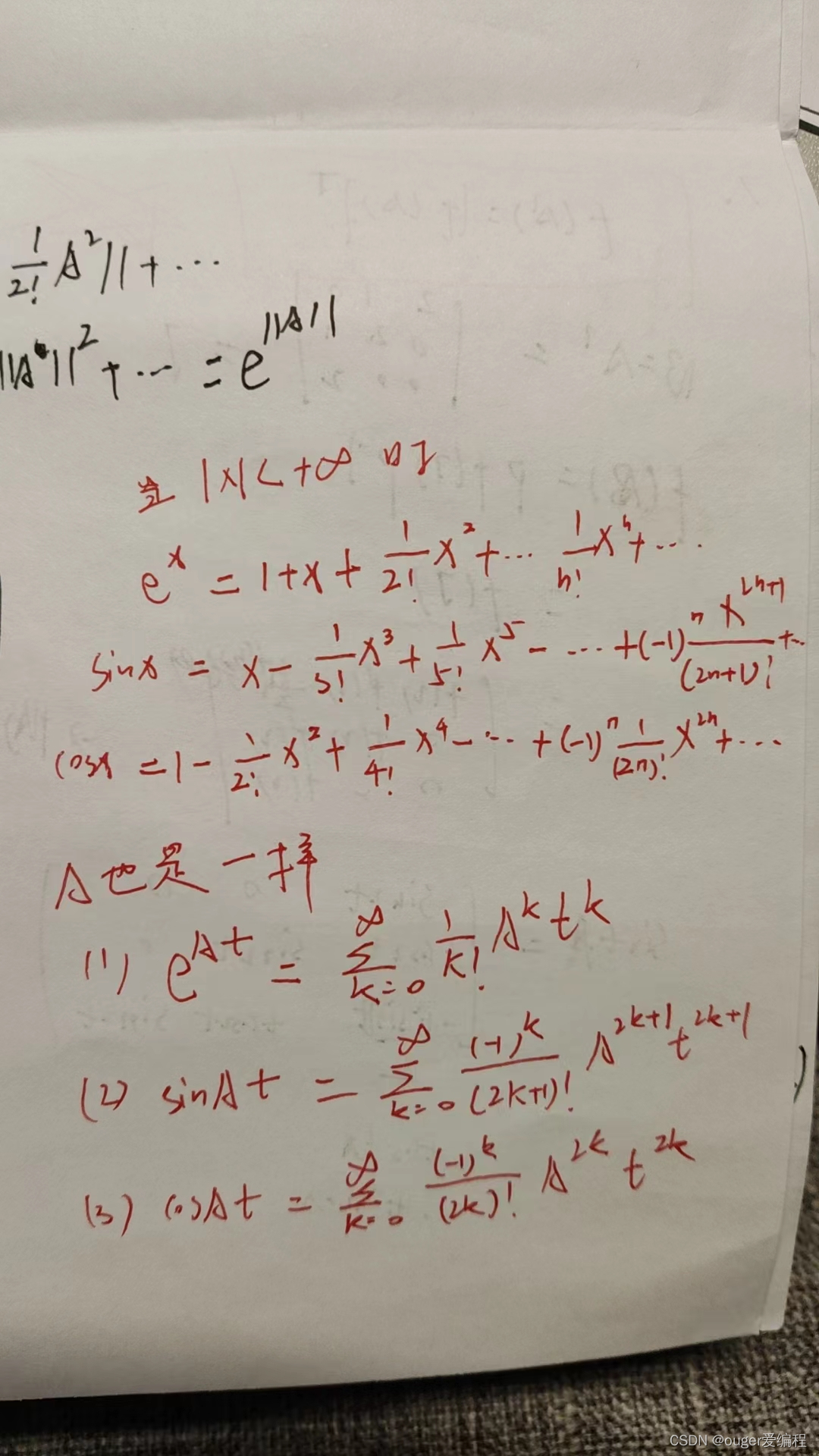
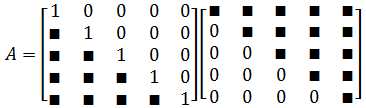

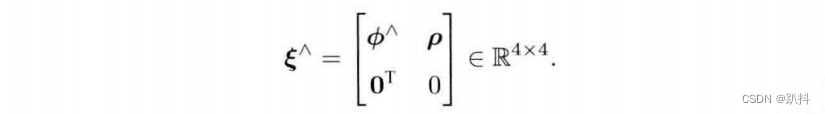




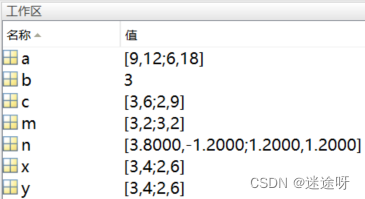
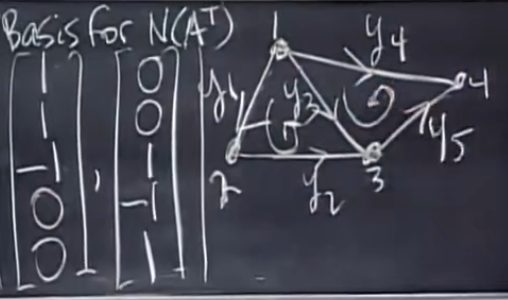
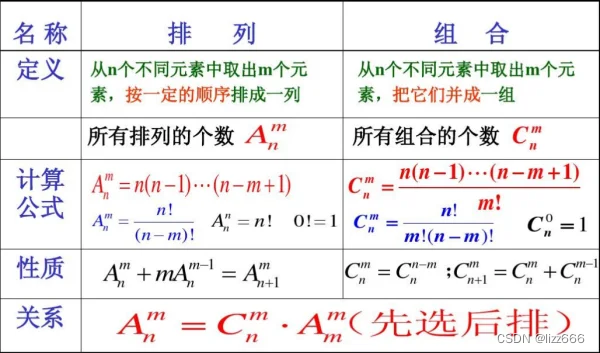


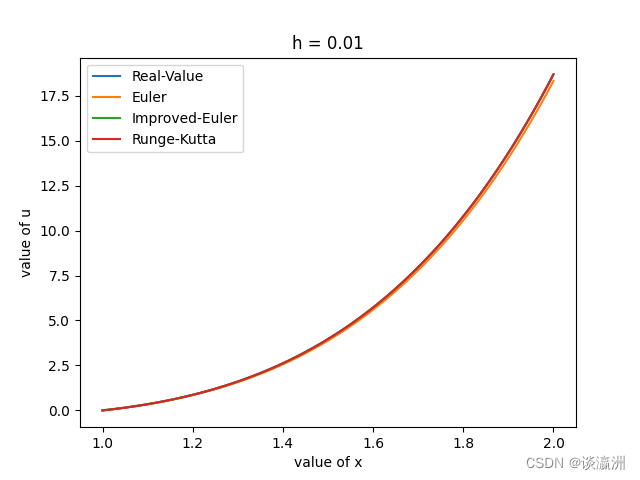
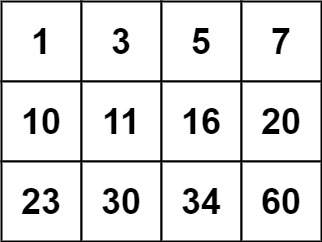
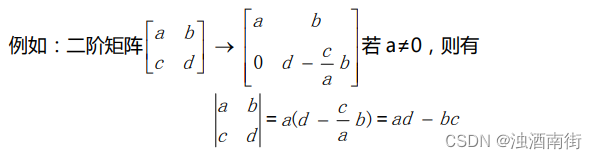



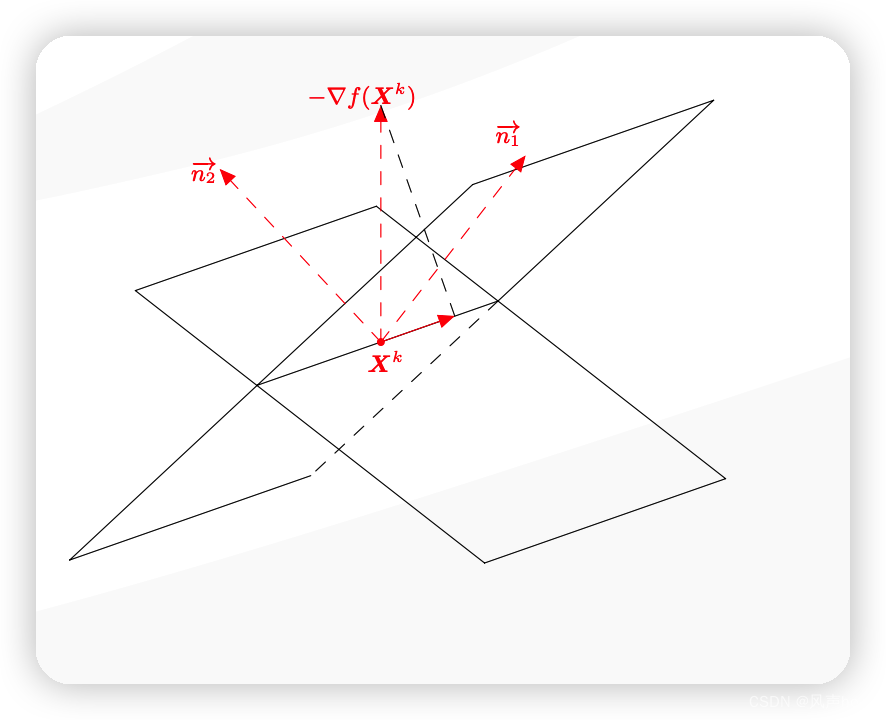

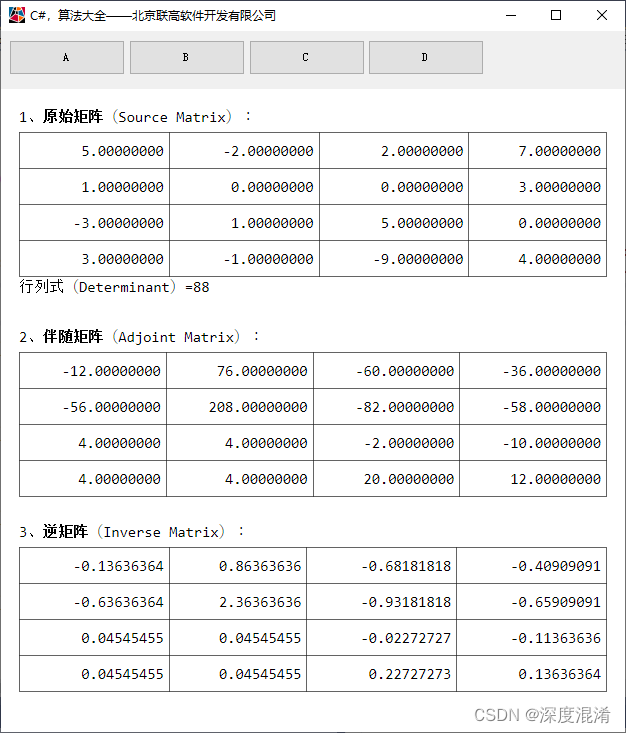
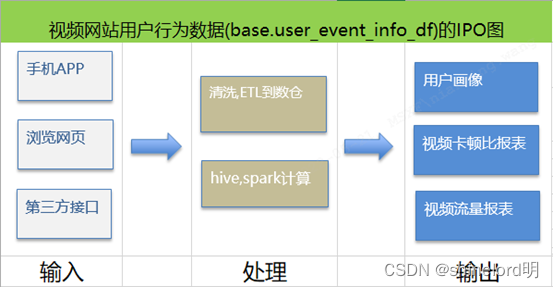


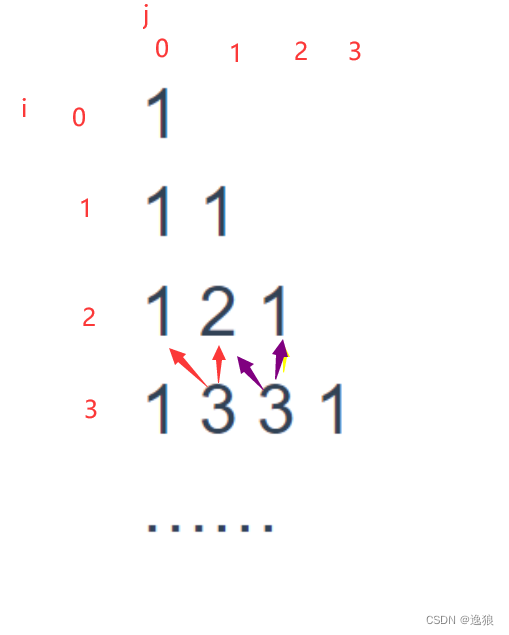







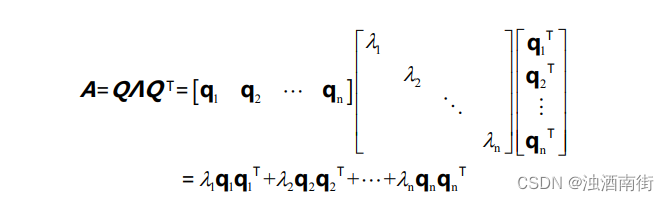









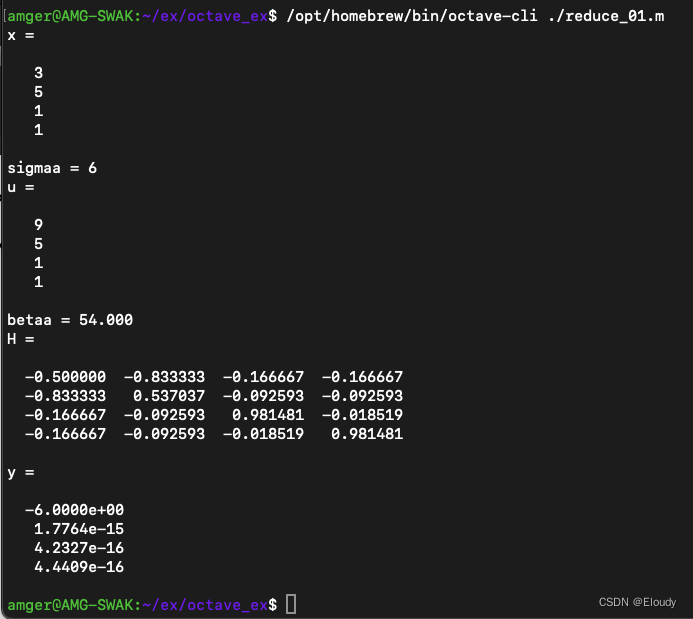

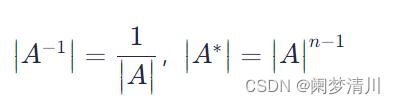
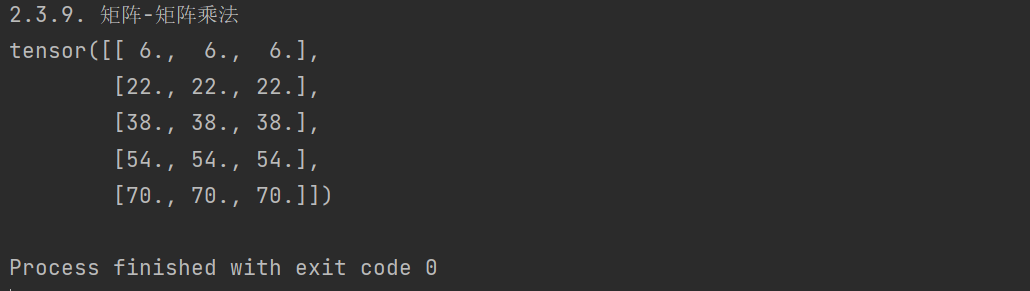




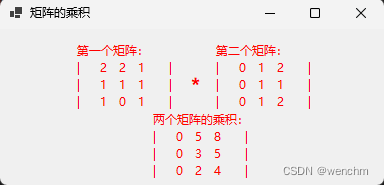




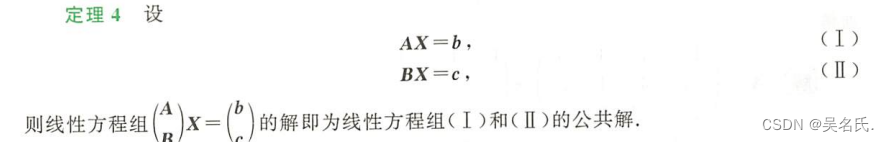
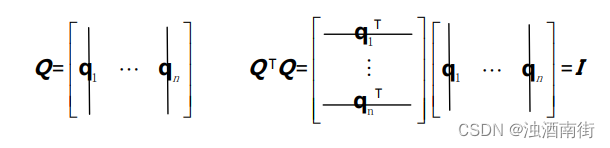



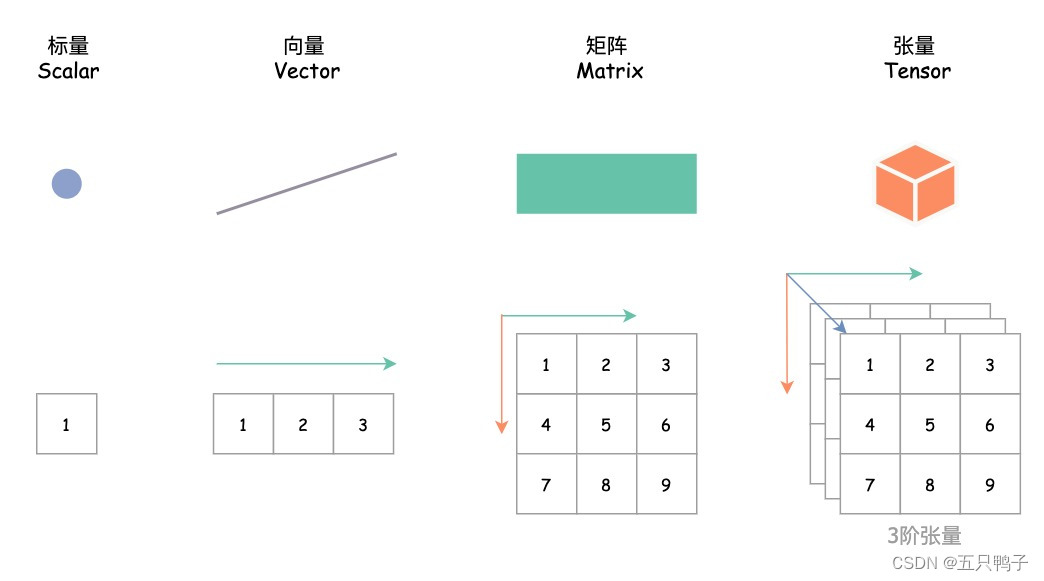




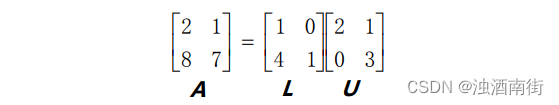


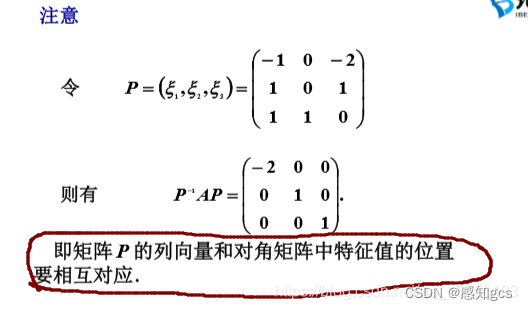


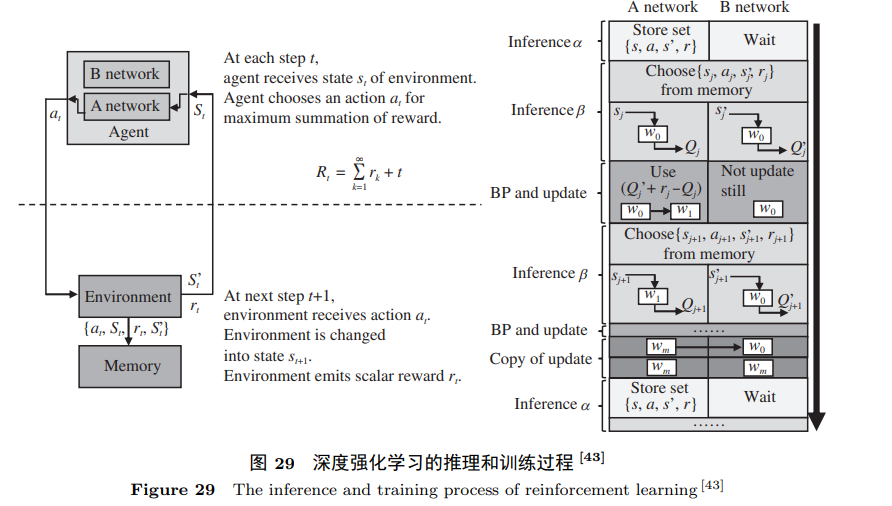

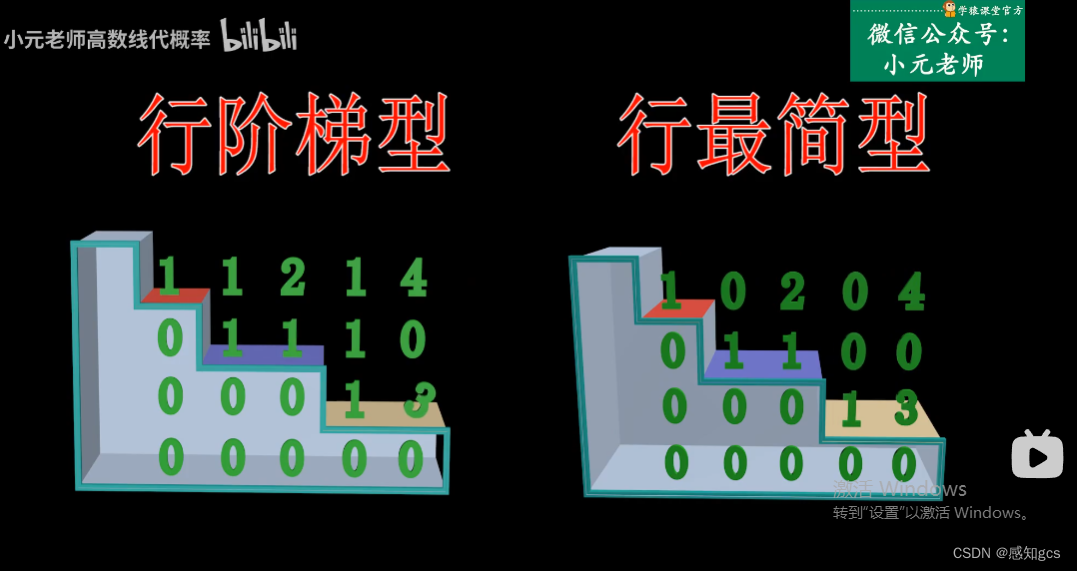
![P9905 [COCI 2023/2024 #1] AN2DL 【矩阵区间最大值】](https://img-blog.csdnimg.cn/direct/4f73e4d86e754d29833b227c5da0e9fa.png#pic_center)

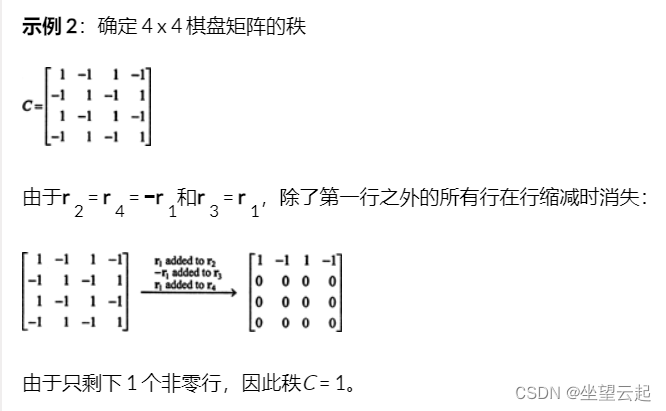
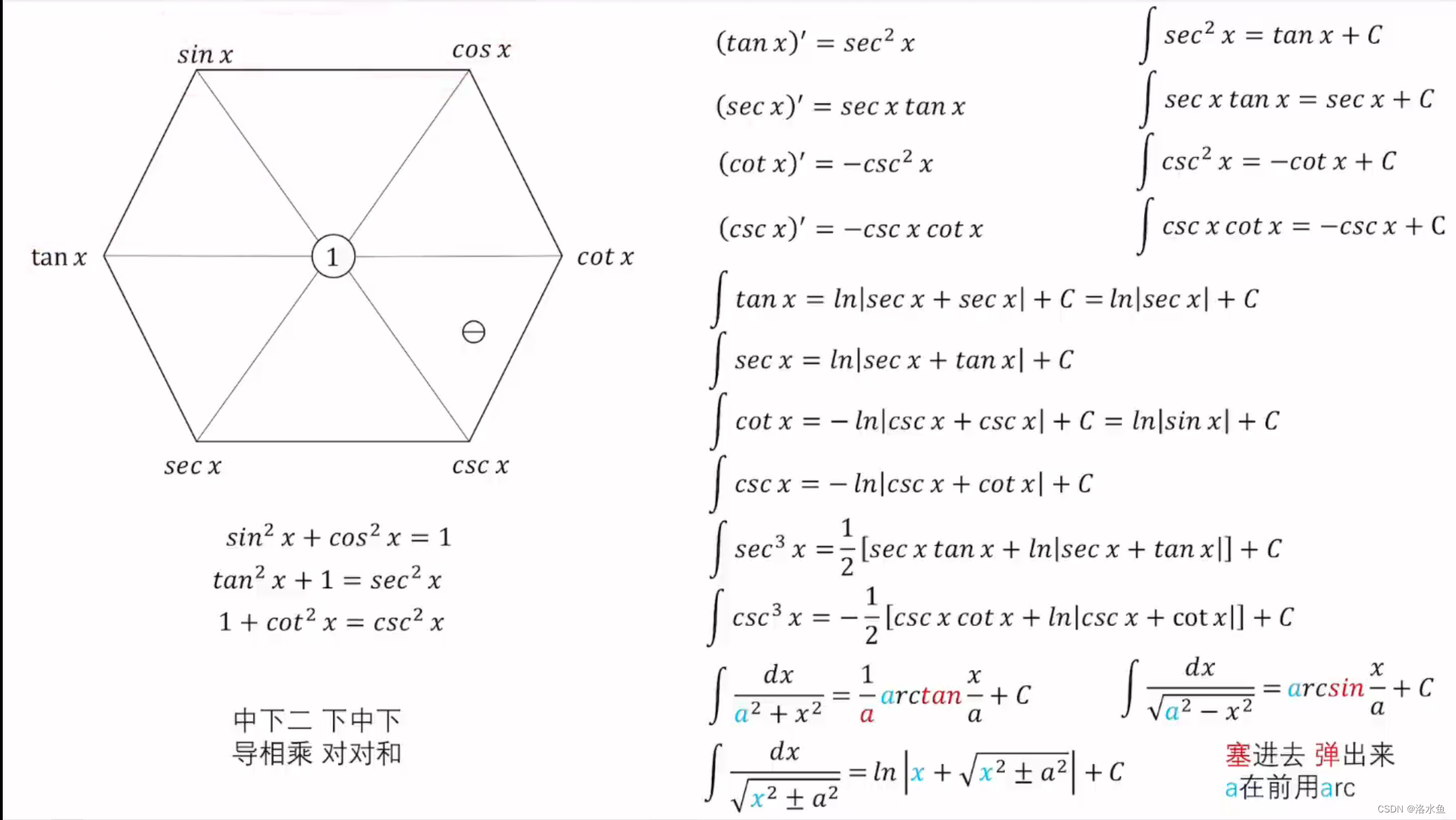

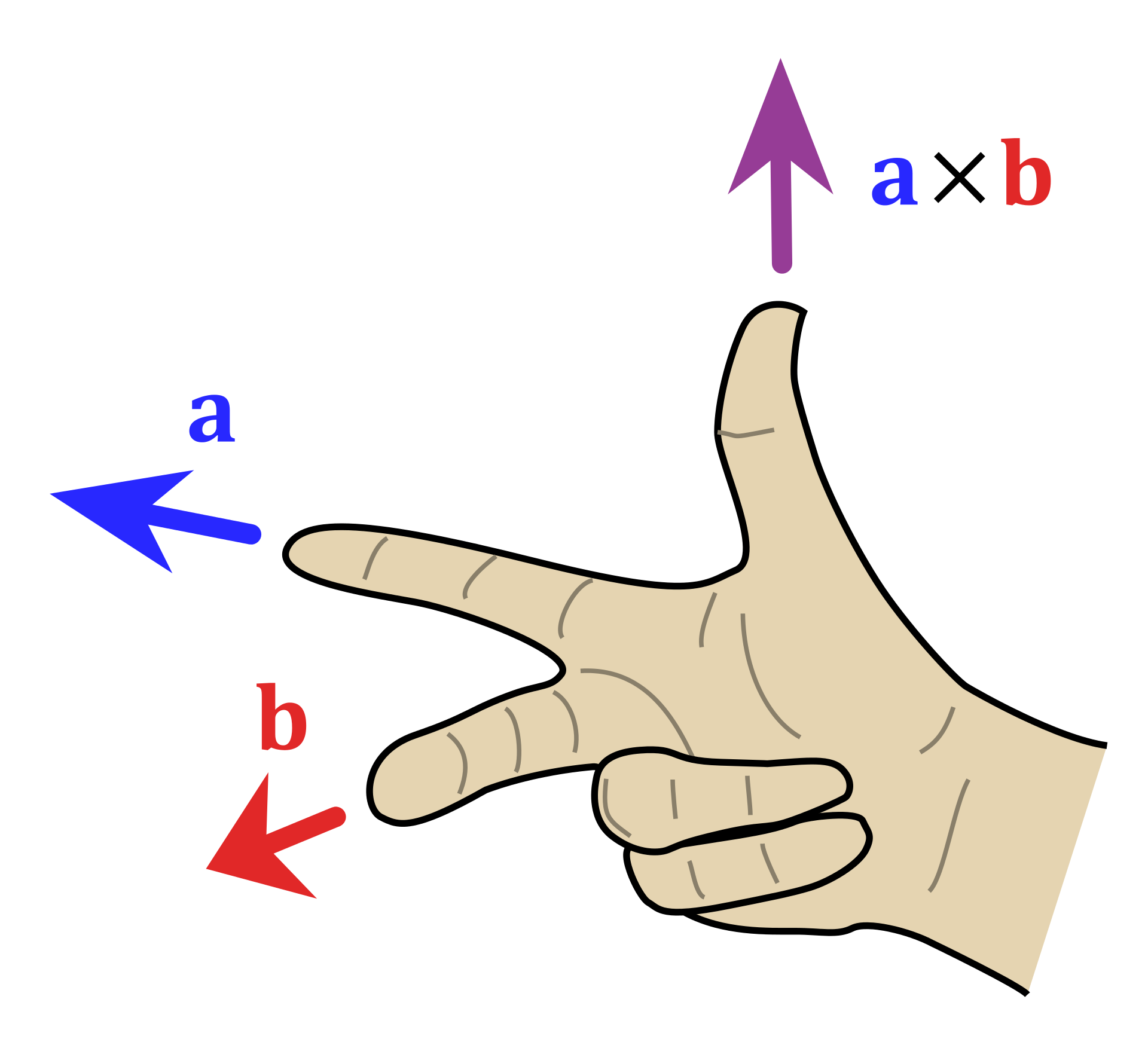
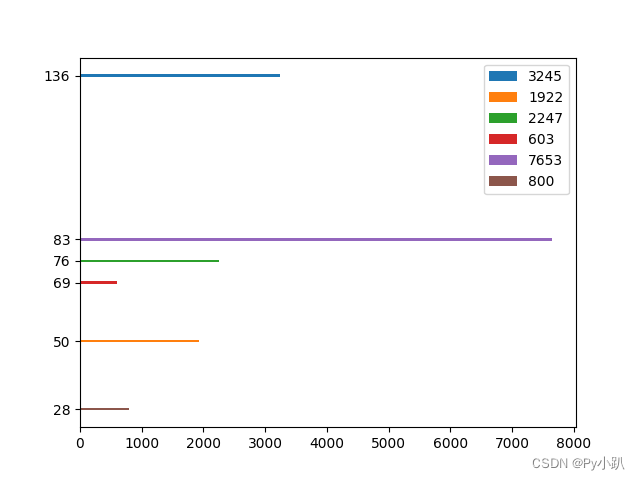





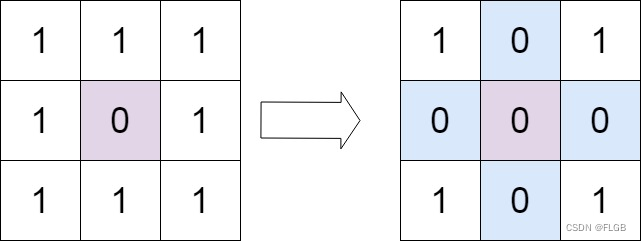

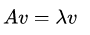


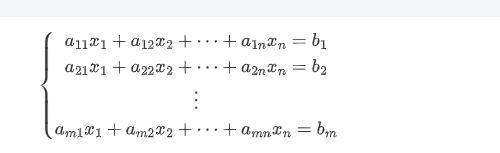

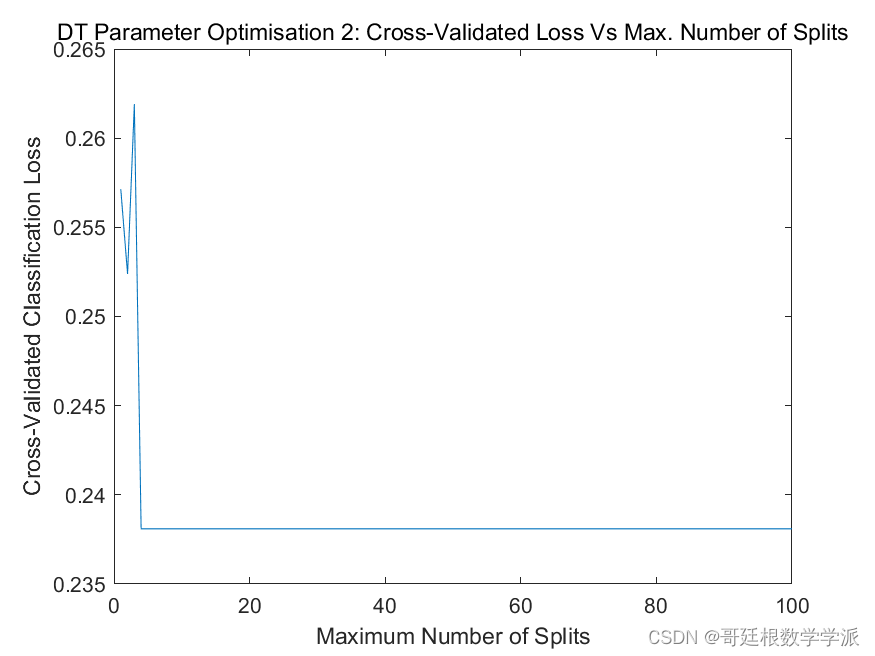

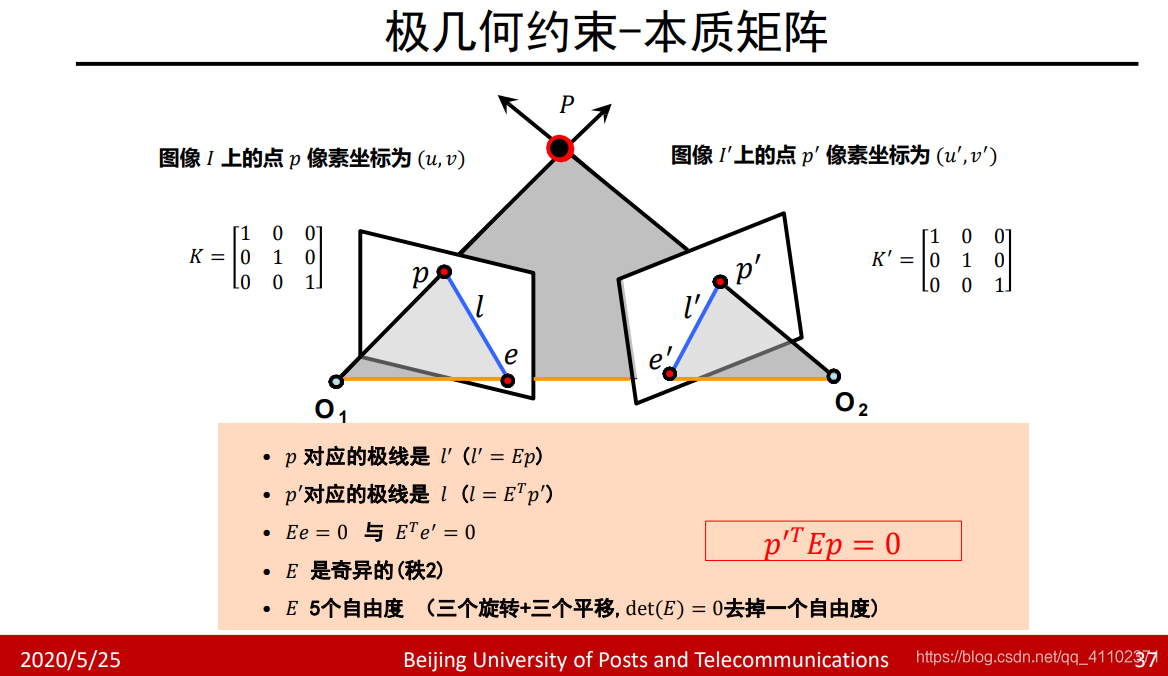



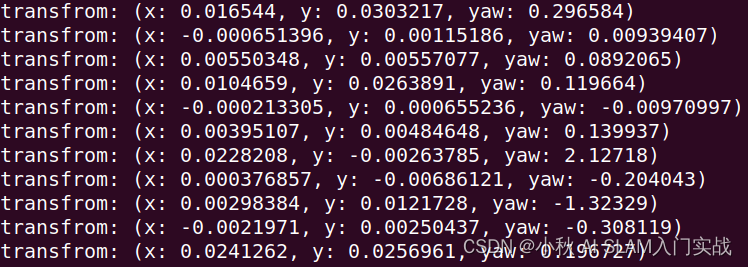

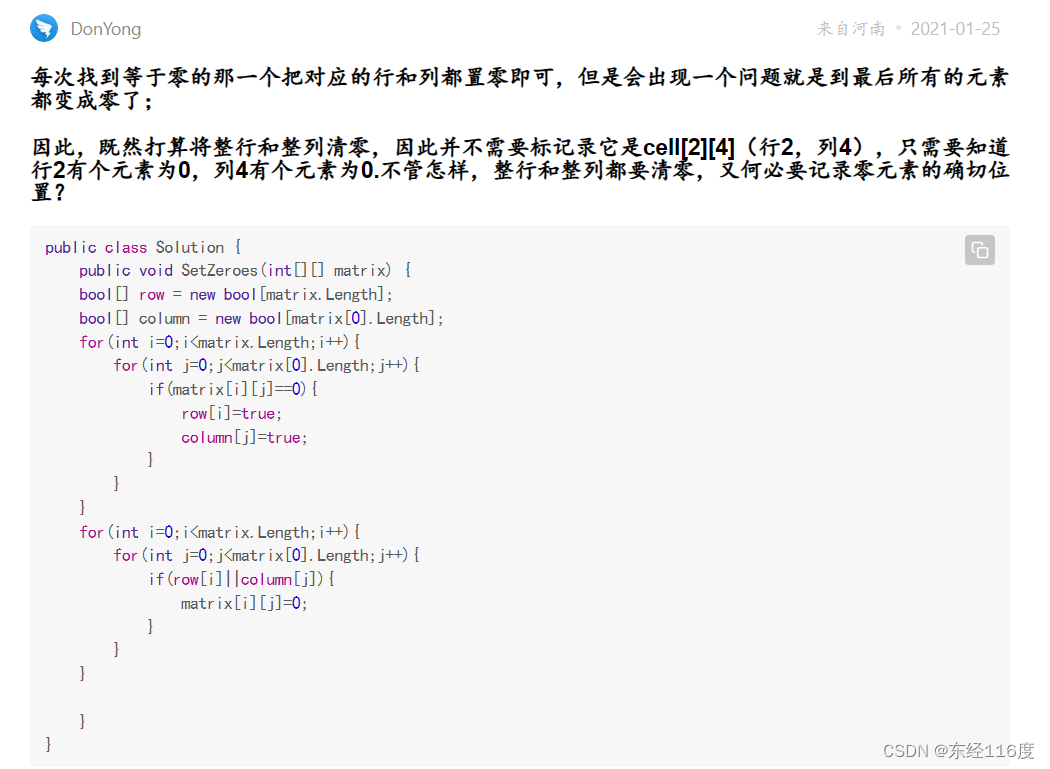
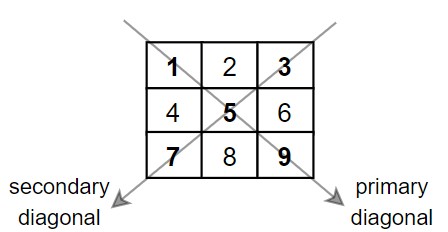

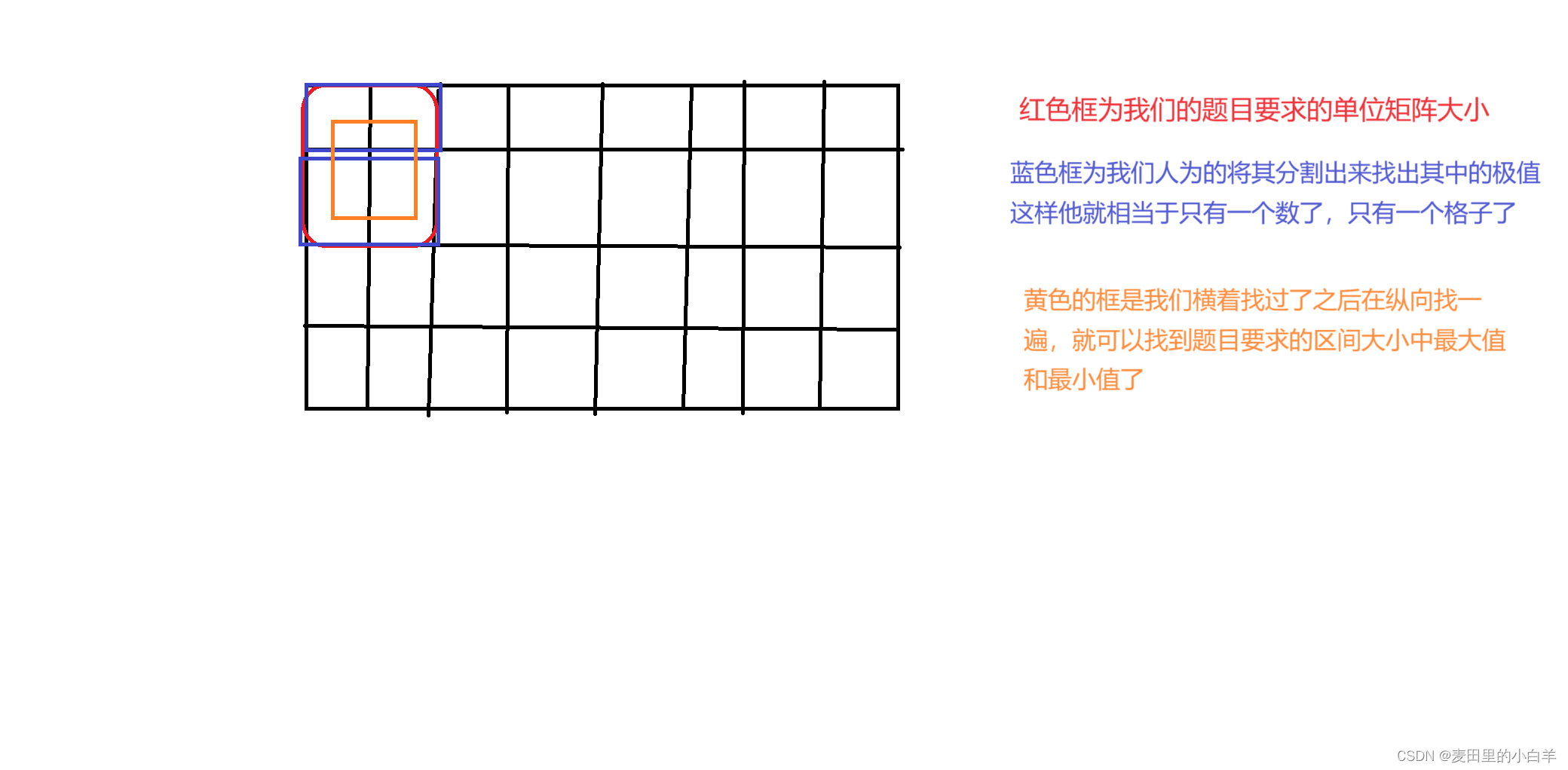
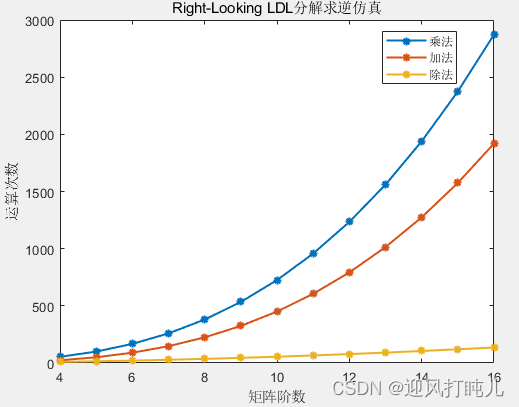

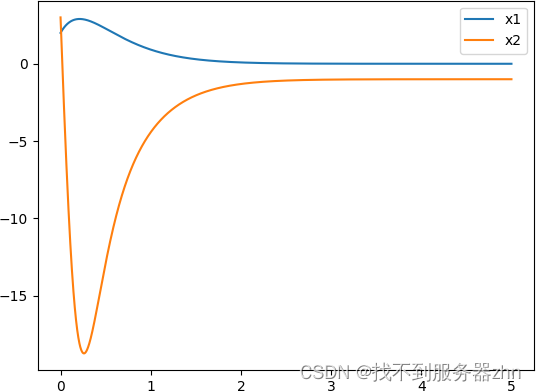

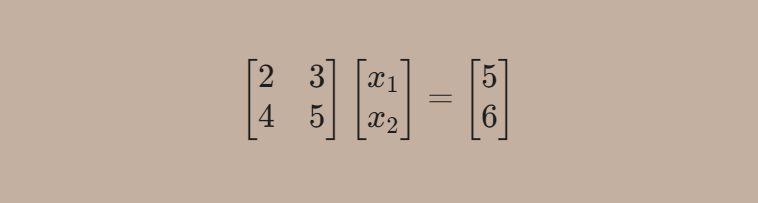




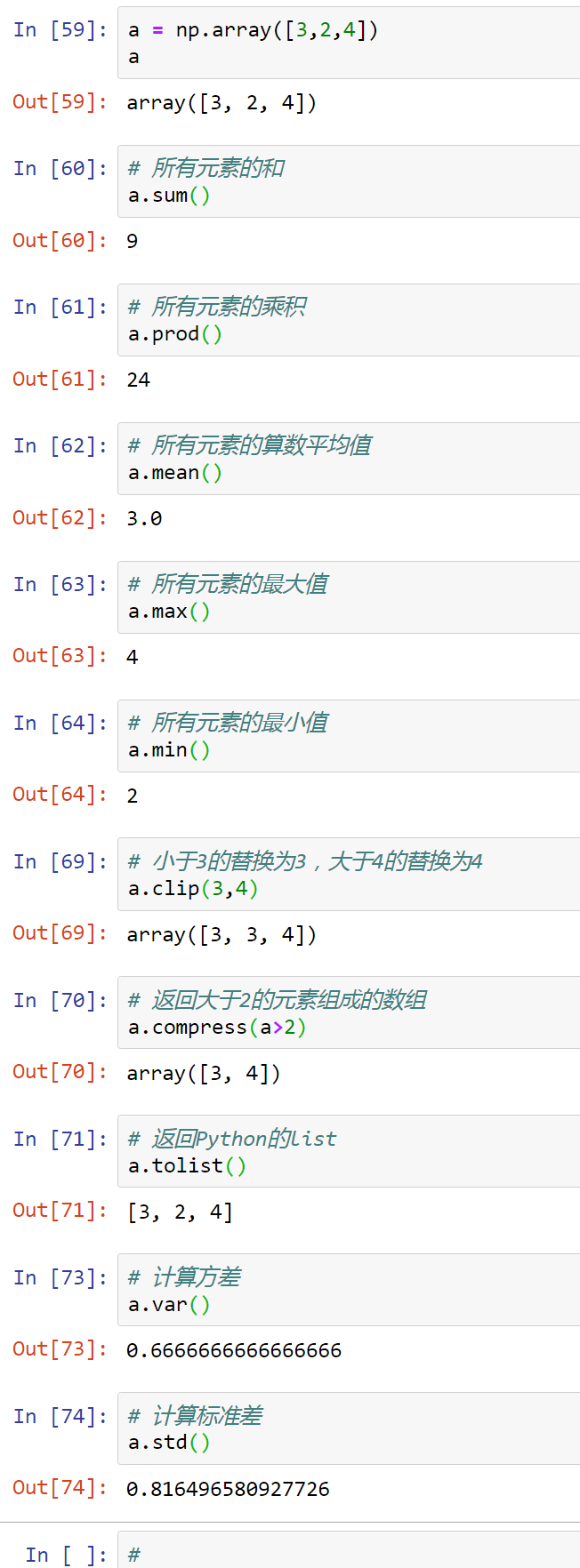


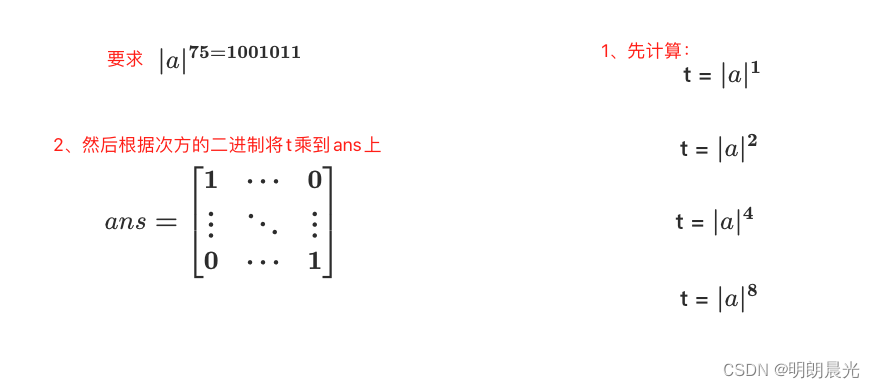
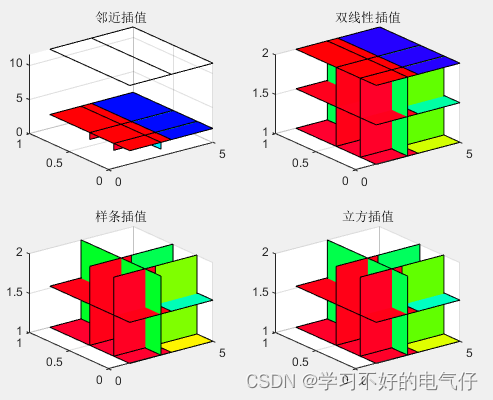
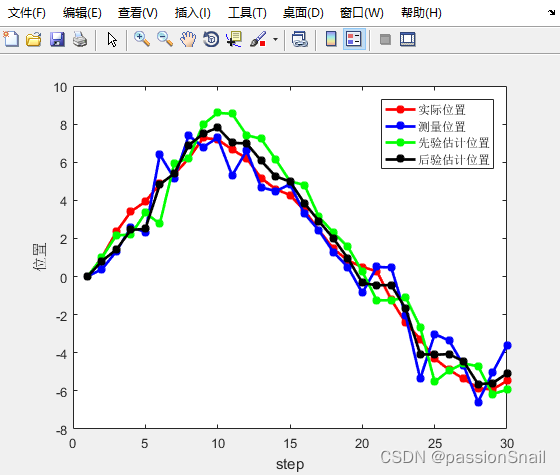
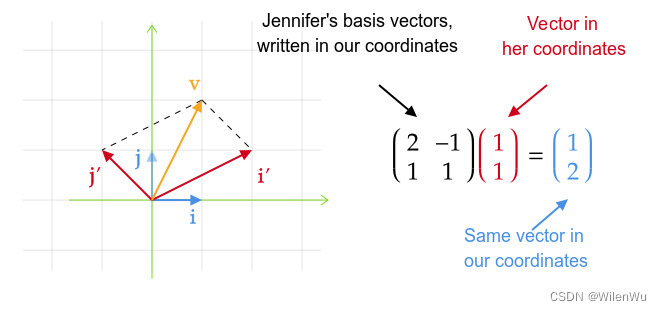



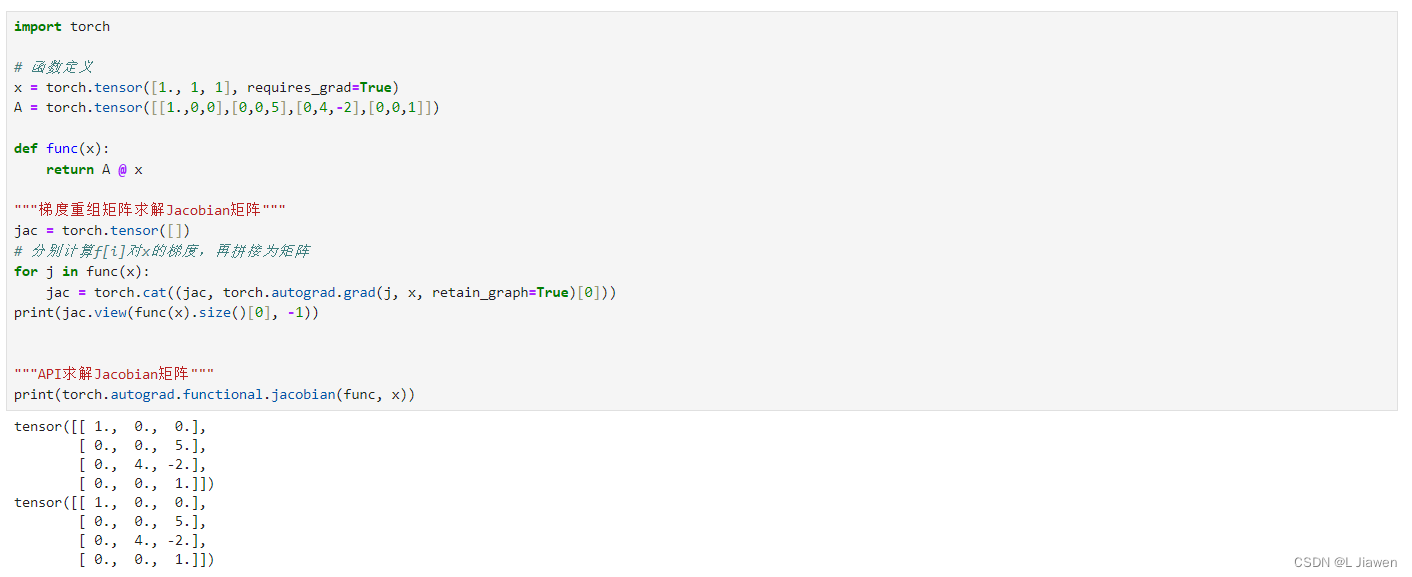


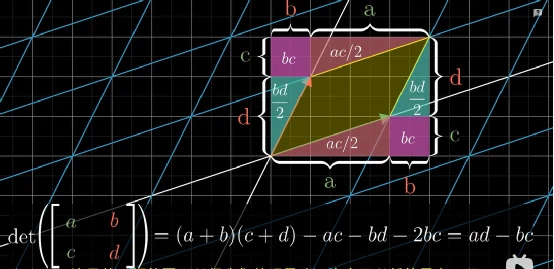
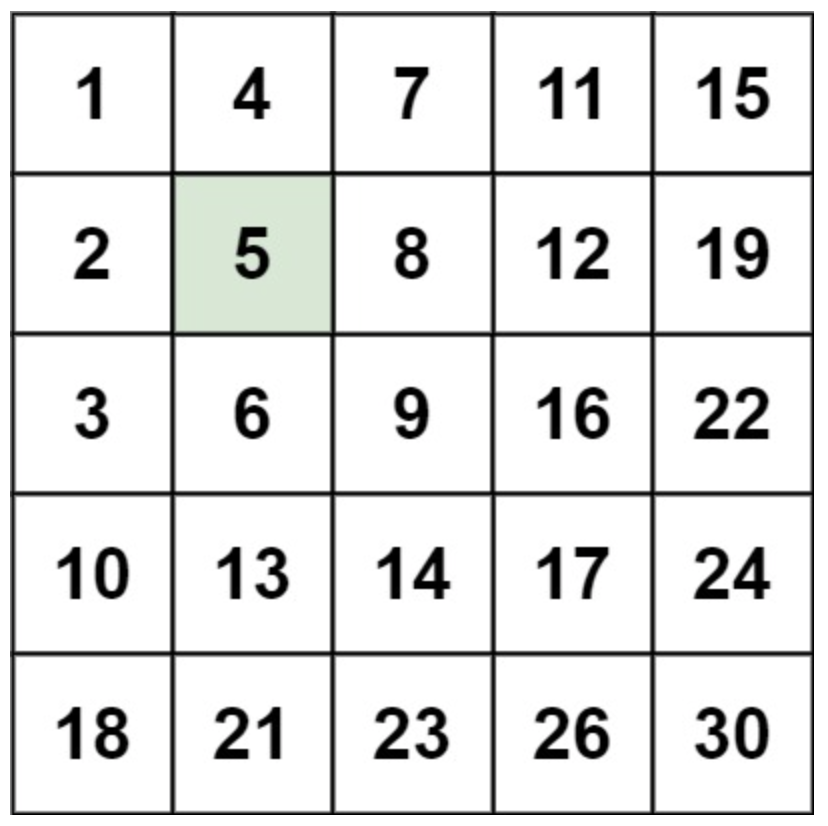


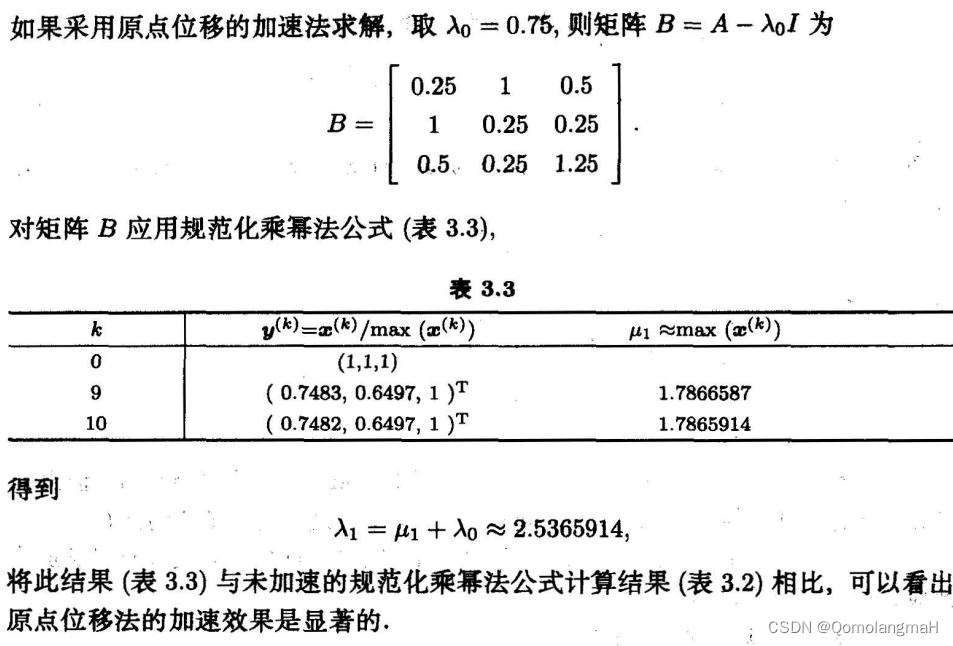

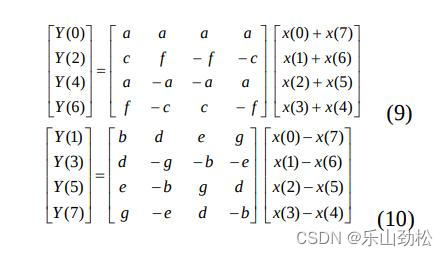
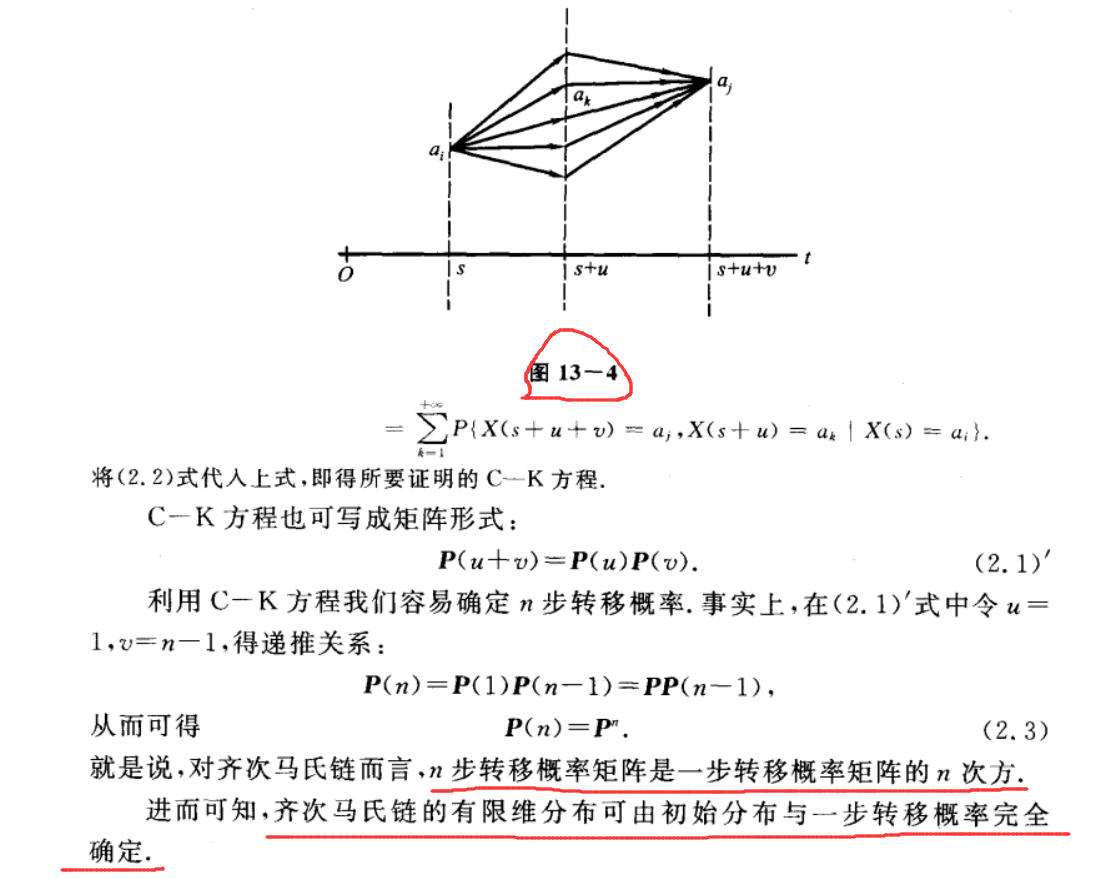







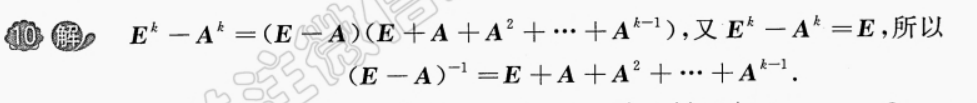
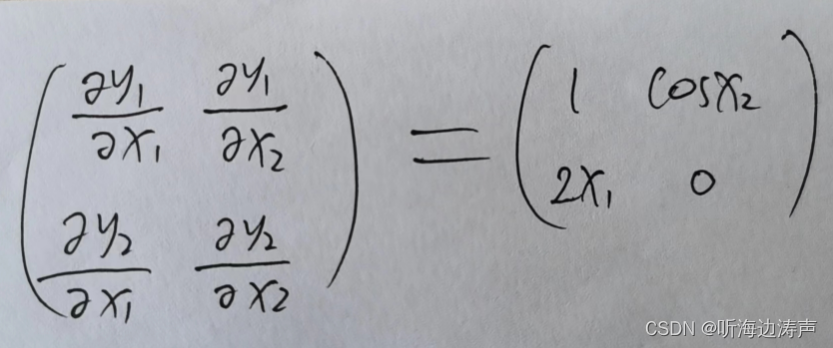

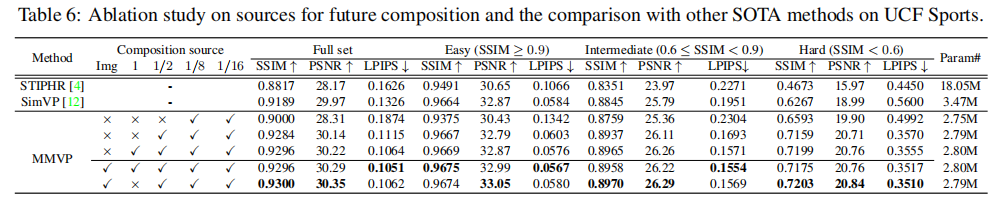
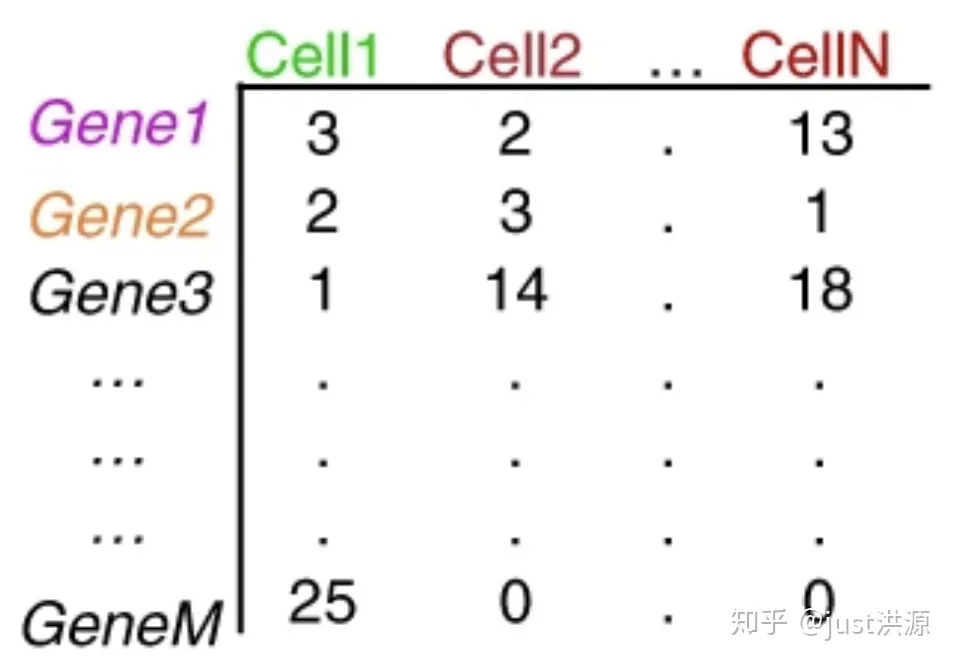


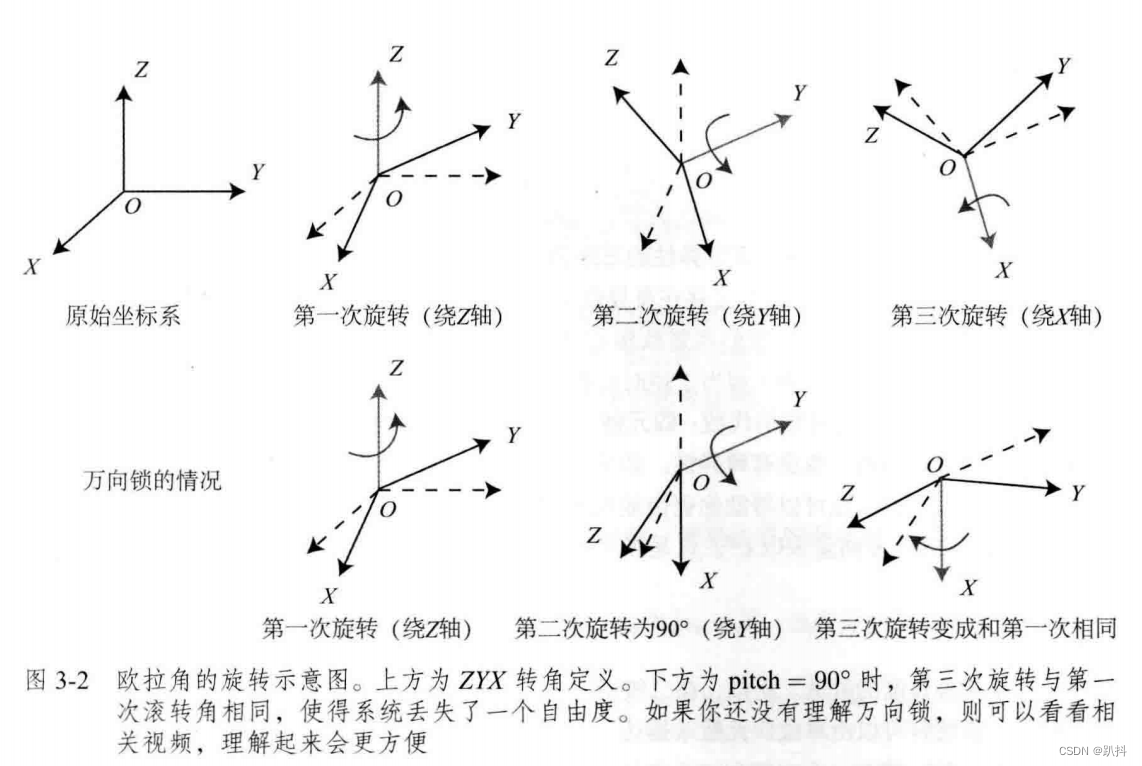



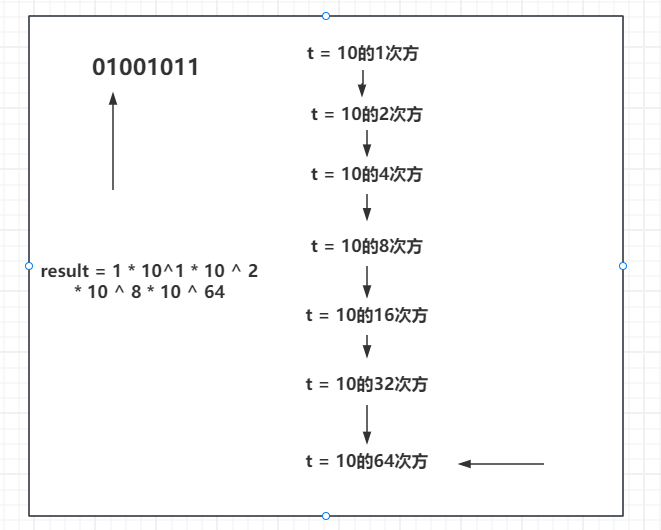






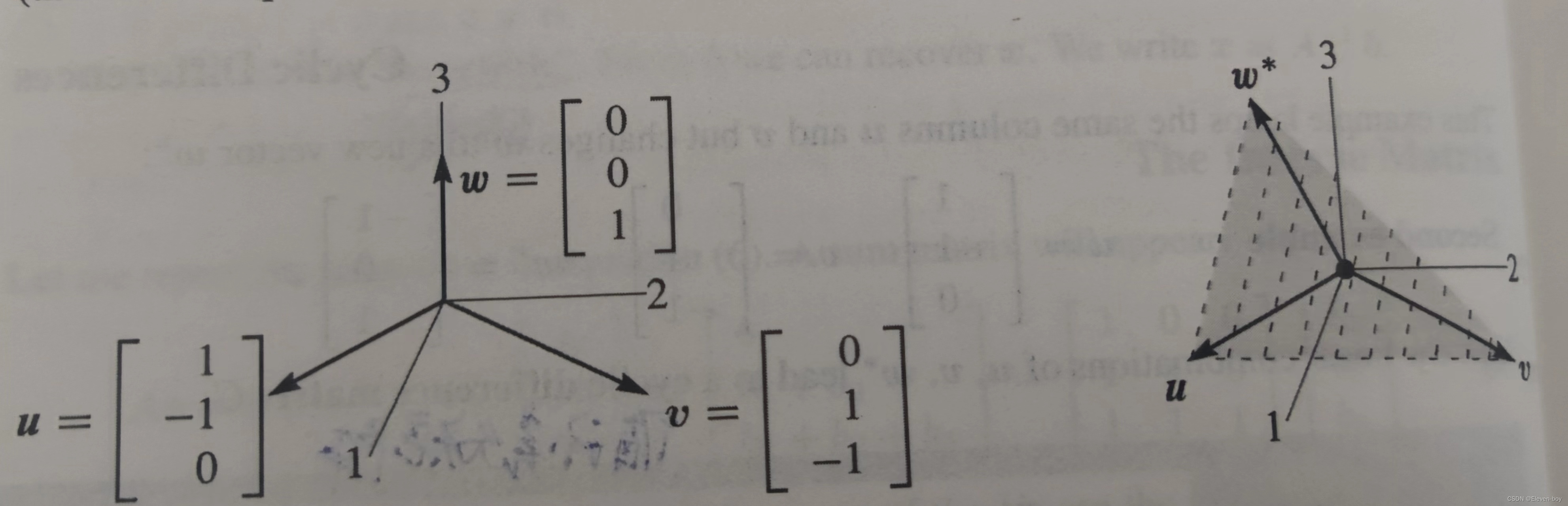


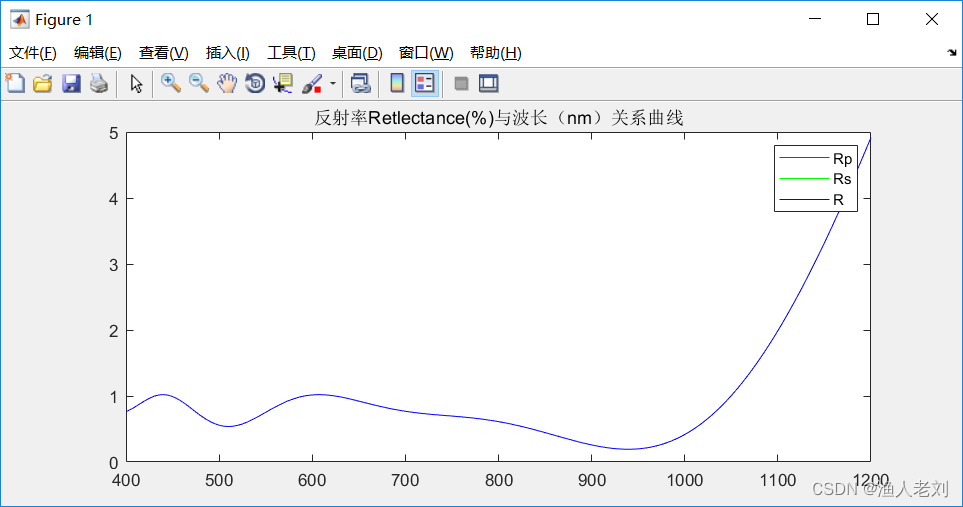
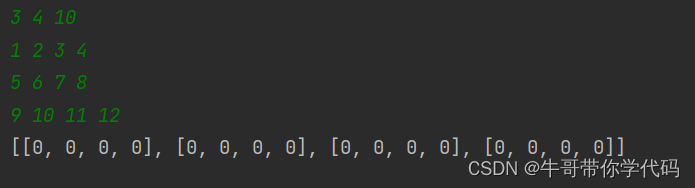
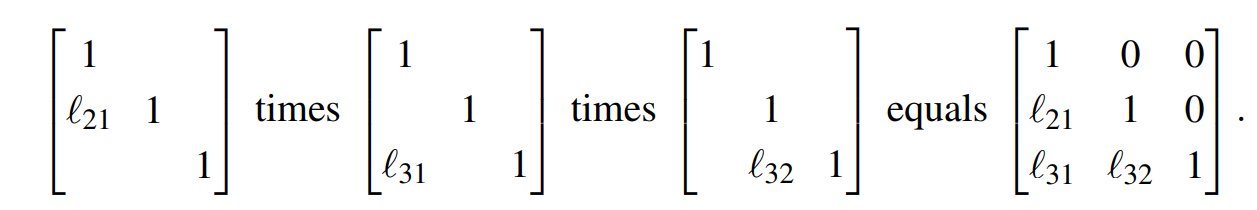

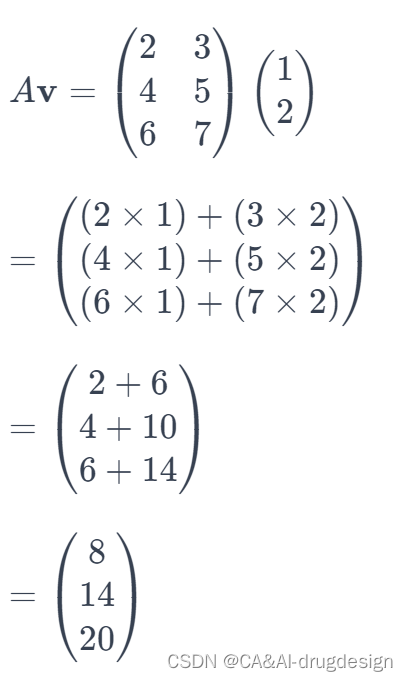




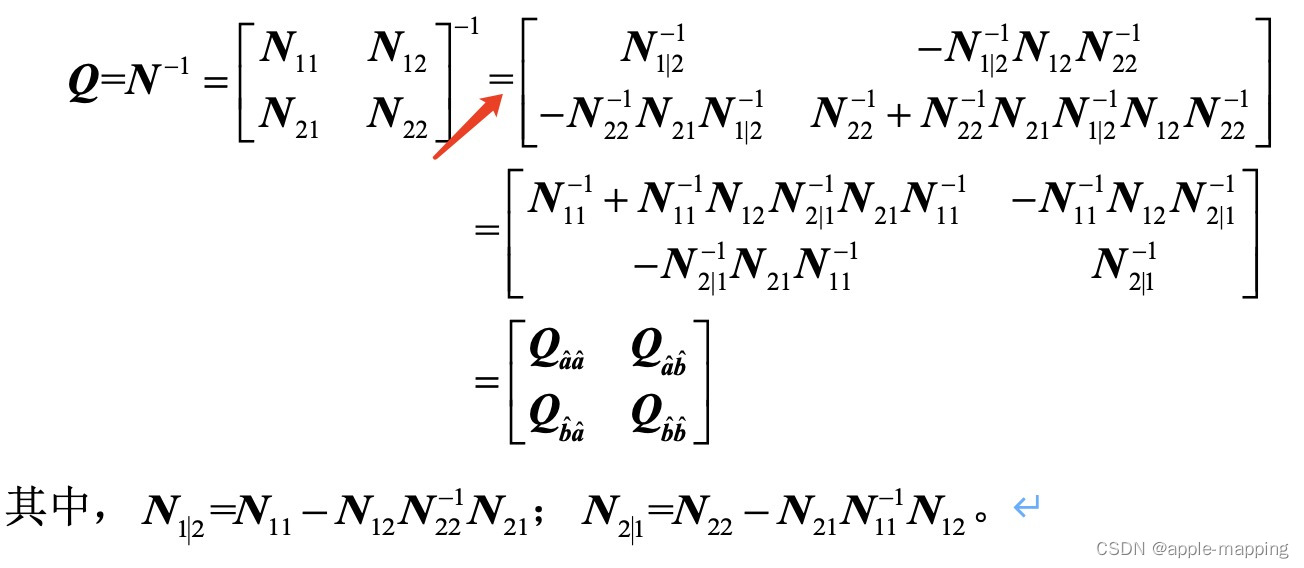

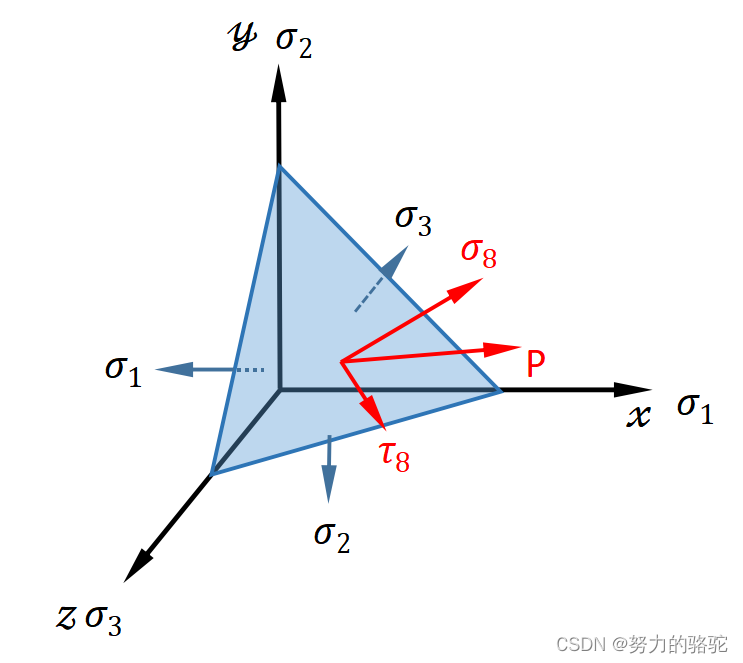
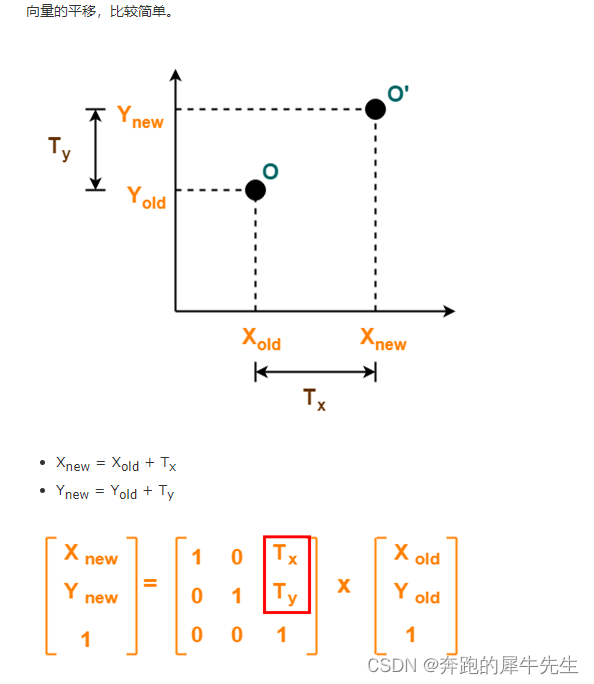
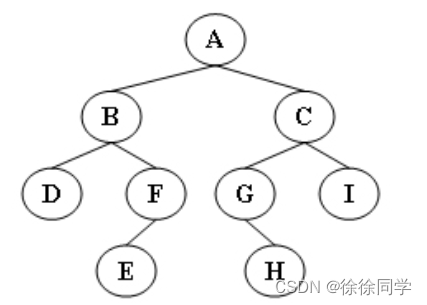

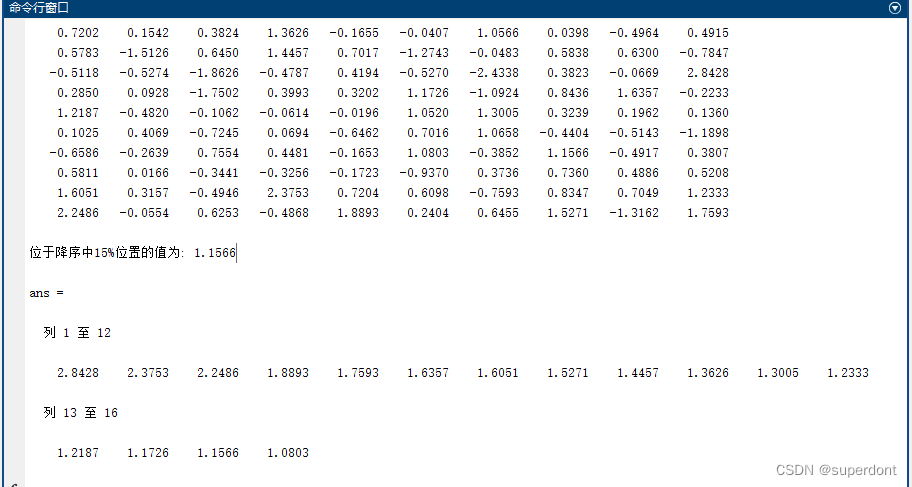
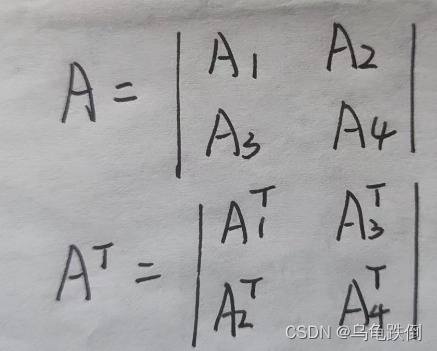




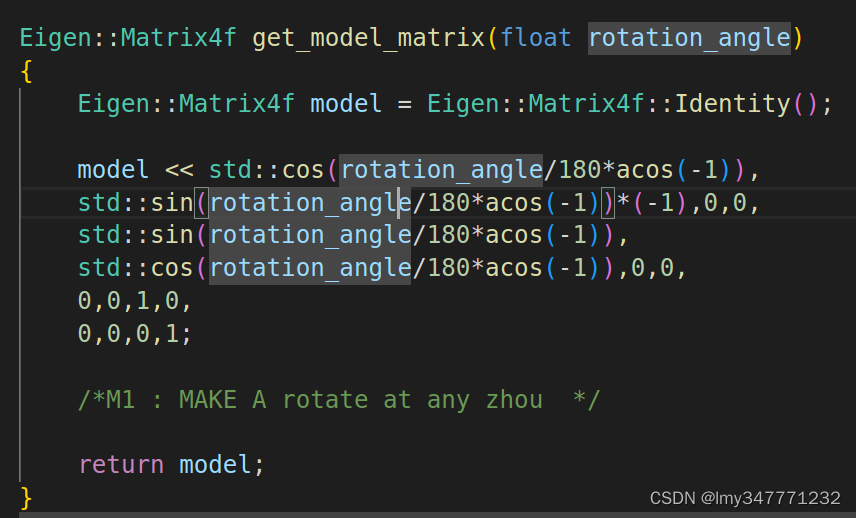

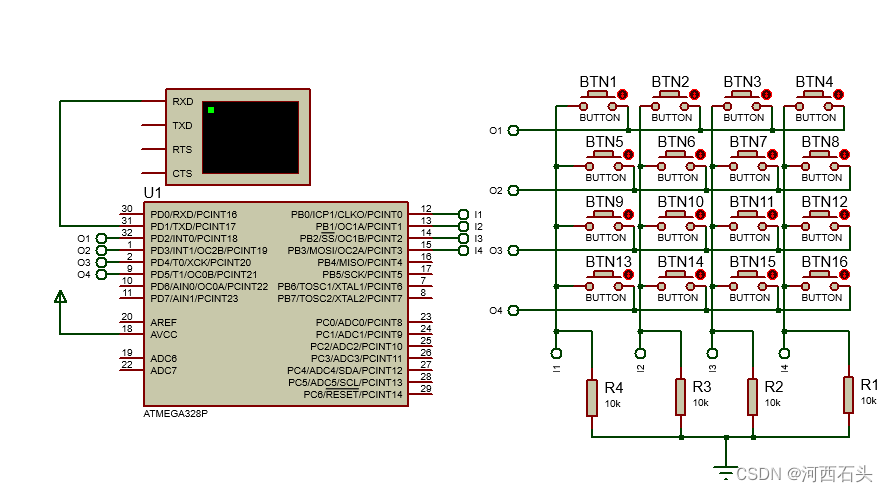
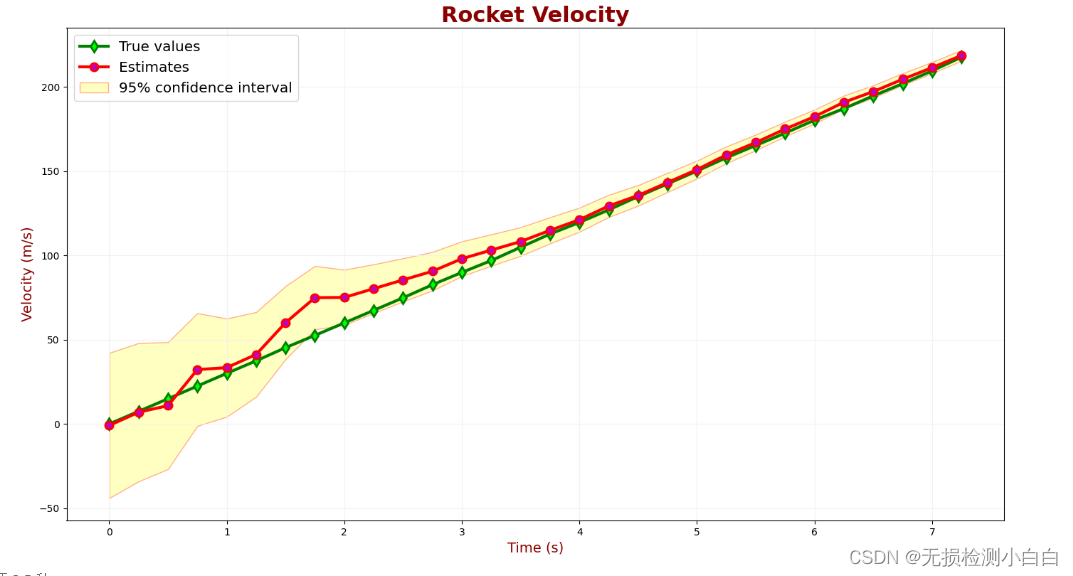
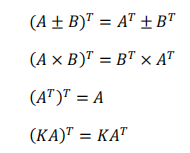

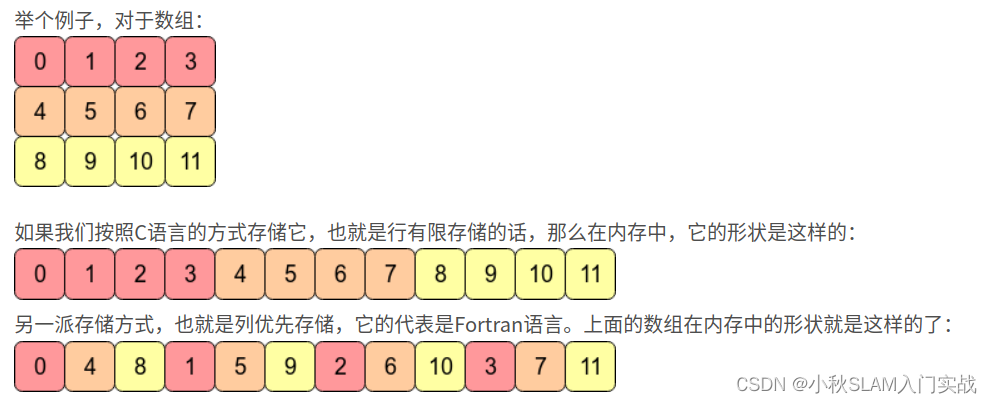




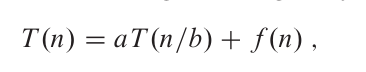
![[坐标系转换]车体坐标系 转 像素坐标系](https://img-blog.csdnimg.cn/095de83465f944c3942b127d7c964161.png)